Les orages

ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée

Sujet 2024 n°SPEPHCH118 et n°SPEPHCH121

Un orage est une perturbation atmosphérique donnant lieu à une décharge électrique violente : la foudre. Celle-ci est généralement accompagnée d’un phénomène lumineux, l’éclair et d’un phénomène sonore, le tonnerre.

Source : Lemonde.fr

Image http://www.meteo-centre.fr/

1. La foudre, un phénomène électrique

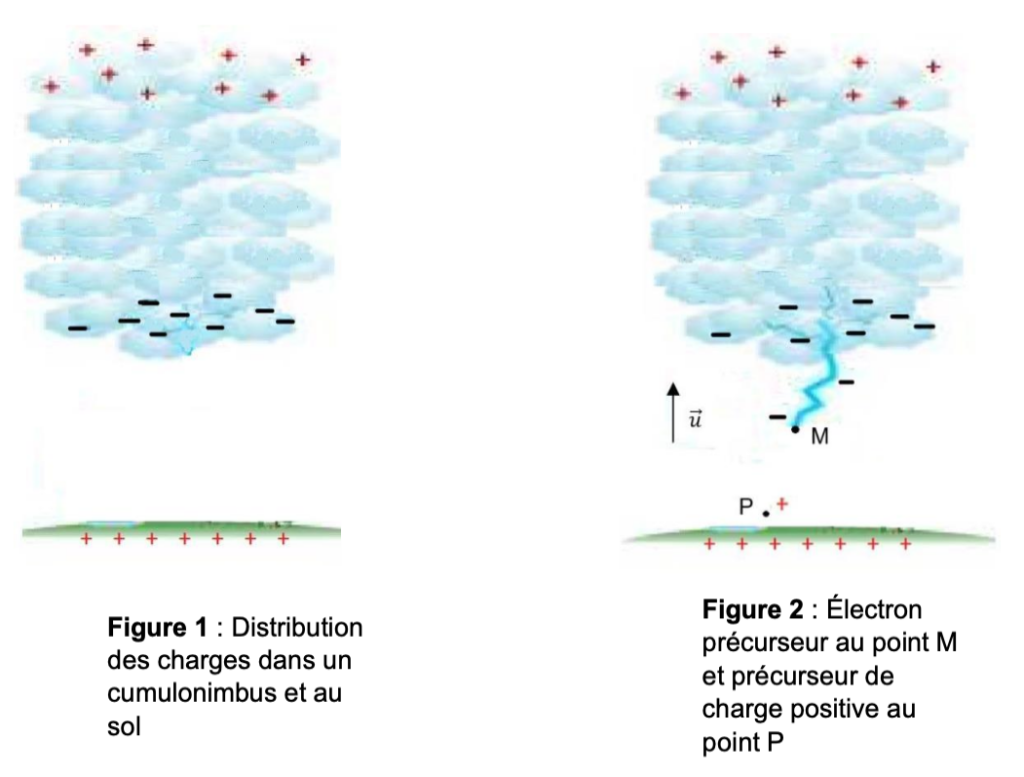
Par temps d’orage, on observe la formation de nuages orageux appelés cumulonimbus. Ils sont le siège de mouvements d’air ascensionnels importants qui créent une accumulation de charges positives au sommet du nuage et de charges négatives à sa base. Au voisinage de la base du nuage, le sol en regard se charge positivement. L’accumulation de charges électriques entre la base du nuage et le sol crée un champ électrique intense, dont la valeur peut atteindre 50 kV/m.

Dans la suite de l’exercice, le champ électrique entre le nuage et le sol est supposé uniforme et de direction verticale.

Données :

Charge électrique élémentaire : 𝑒 = 1,6 × 10⁻¹⁹ 𝐶

1.1. Indiquer si le sol se charge par contact ou par influence.

Il n’y a pas de contact entre le nuage et le sol : le sol se charge par influence.

1.2. Sur la figure 1 de l’ANNEXE À RENDRE AVEC LA COPIE, représenter quelques lignes de champ électrique dans la zone en pointillés entre le sol et la base du nuage.

Les lignes qui sont tangentes au vecteur champ et orientées dans le même sens que lui donc du + (sol) vers le — (nuage).

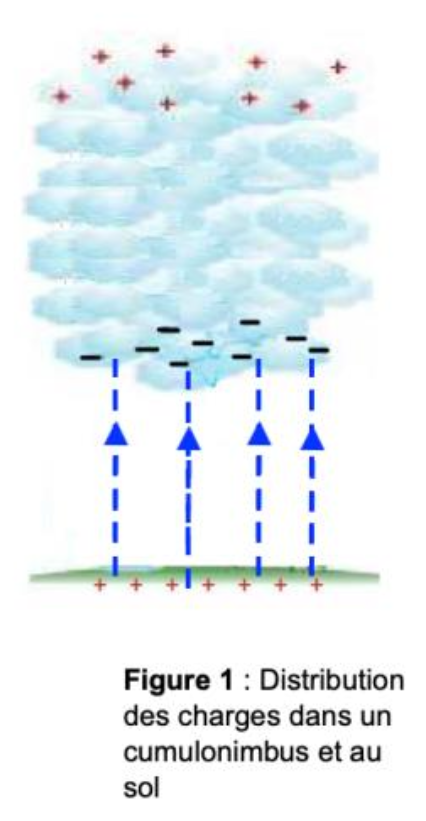
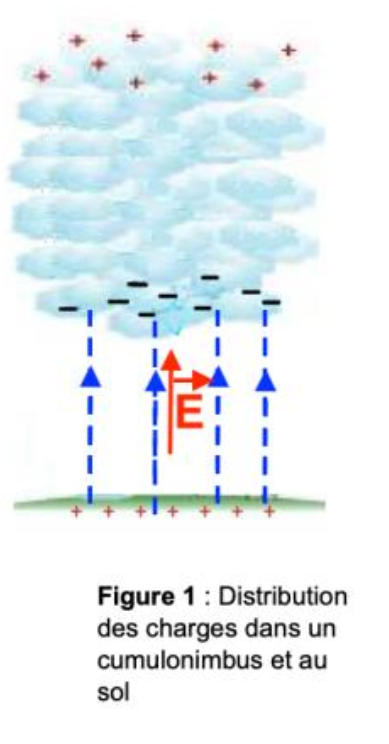
1.3. Sur la figure 1 de l’ANNEXE À RENDRE AVEC LA COPIE, représenter le vecteur champ électrique $\overrightarrow{E}$ en un point quelconque de cette zone, sans considération d’échelle.

Le vecteur champ électrique $\overrightarrow{E}$ est perpendiculaire au sol et dirigé du + (sol) vers le — (nuage).

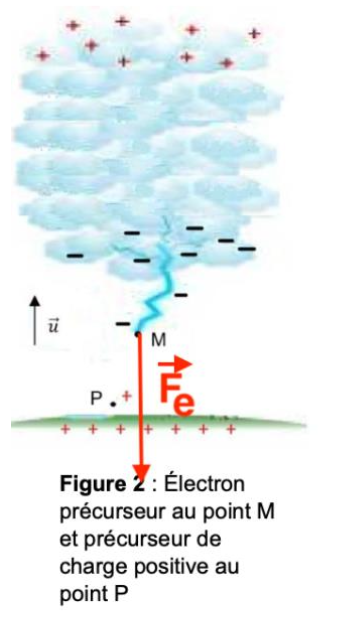
Le champ électrique entre le sol et la base du nuage est si intense que l’air peut être ionisé ce qui permet le passage d’une décharge électrique : la foudre. La foudre est initiée par le mouvement de porteurs de charge électrique que l’on nomme précurseurs. Les précurseurs de la base du nuage sont des électrons qui se déplacent vers le sol d’une centaine de mètres. Au niveau du sol, le phénomène réciproque peut avoir lieu. Les précurseurs sont alors des porteurs de charge positive, qui se déplacent vers le nuage. Les précurseurs qui se rejoignent vont permettre le passage de la foudre.

1.4. Donner l’expression vectorielle de la force électrique $\overrightarrow{F_e}$ s’exerçant sur un électron précurseur et calculer la valeur de sa norme $\overrightarrow{E}$ pour un champ électrique de 50 kV/m. Le vecteur unitaire utilisé $\overrightarrow{u}$ est indiqué sur la figure 2 sur l’ANNEXE À RENDRE AVEC LA COPIE.

$\mathrm{\overrightarrow{F_e} = q \times \overrightarrow{E}}$

$\mathrm{q = -e}$

D’où

$\mathrm{\overrightarrow{F_e} = -e \times \overrightarrow{E}}$

Le signe – indique qu’ils ont des sens opposés.

Calculons la valeur :

$\mathrm{F_e = e \times E }$

$\mathrm{F_e = 1{,}60 \times 10^{-19} \times 50 \times 10^3 }$

$\mathrm{F_e = 8{,}0 \times 10^{-15} \, \text{N}}$

1.5. Sur le schéma de la figure 2 de l’ANNEXE À RENDRE AVEC LA COPIE, représenter la force électrique s’exerçant sur un électron précurseur placé au point M et celle s’exerçant sur un précurseur de charge électrique (+e) placé au point P à l’échelle de 1,0 cm pour 4,0×10^-15 N.

$\mathrm{ \overrightarrow{F_e} = -e \times \overrightarrow{E}}$

$\overrightarrow{F_e}$ et $\overrightarrow{E}$ sont colinéaires, les deux overrightarrowteurs ont la même direction.

Le signe $-$ indique qu’ils ont des sens opposés.

$\mathrm{ x = \frac{(8{,}0 \times 10^{-15} \times 1{,}0)}{4{,}0 \times 10^{-15}}}$

$\mathrm{ x = 2{,}0 \, \text{cm}}$

Traçons $\overrightarrow{F_e}$ :

– Point d’application : point M

– Direction : même direction que $\overrightarrow{E}$ . Perpendiculaire au sol.

– Sens : sens opposé à $\overrightarrow{E}$ . Perpendiculaire au sol. Du – (nuage) vers le + (sol).

– Valeur : $F_e = 8{,}0 \times 10^{-15} \, \text{N}$ . Représenté par un vecteur de $2{,}0 \, \text{cm}$ .

2. Modélisation de la foudre et aspect énergétique

Pour une tension électrique entre le nuage et le sol de 50 MV, la foudre correspond à la circulation de l’ordre de 10²¹ porteurs de charges électriques élémentaires pendant à peine 25 ms !

On modélise le passage de la foudre à travers l’air par un courant électrique constant circulant à travers un conducteur ohmique.

Donnée :

1 kWh = 3,6 MJ

2.1. Estimer la valeur de l‘intensité du courant électrique associé à la circulation des porteurs de charges électriques durant un coup de foudre.

$\mathrm{I = \frac{Q}{\Delta t}}$

Or,

$\mathrm{Q = N \times e}$

$\mathrm{I = \frac{N \times e}{\Delta t}}$

$\mathrm{I = \frac{10^{21} \times 1,60 \times 10^{-19}}{25 \times 10^{-3}}}$

$\mathrm{I = 6,4 \times 10^3 \, \text{A}}$

L’intensité du courant a pour valeur 6,4×10³ A.

2.2. Estimer la valeur de la résistance électrique du conducteur ohmique modélisant l’air traversé par la foudre.

Loi d’Ohm :

$\mathrm{ U = R \times I }$

D’où :

$\mathrm{ R = \frac{U}{I} }$

$\mathrm{ R = \frac{50 \times 10^6}{6,4 \times 10^3}}$

$\mathrm{ R = 7,8 \times 10^3 \, \Omega}$

2.3. Comparer la valeur obtenue à la question 2.2 avec celle de la résistance électrique du corps humain estimée à quelque milliers d’ohms.

La résistance électrique du corps humain estimée à quelques milliers d’ohms soit en ordre de grandeur.

La résistance électrique du conducteur ohmique modélisant l’air traversé par la foudre est de en ordre de grandeur.

Ainsi, la résistance électrique du conducteur ohmique est plus grande que la résistance électrique du corps humain.

Un orage compte en moyenne une centaine de coups de foudre et on dénombre chaque année sur l’ensemble du territoire français de l’ordre de dix mille orages.

2.4. Vérifier qu’un coup de foudre dégage une énergie de 8×10⁹J.

L’énergie est définie par :

$\mathrm{ E = P \times \Delta t }$

La puissance électrique est définie par :

$\mathrm{ P = U \times I }$

D’ou

$\mathrm{ E = U \times I \times \Delta t }$

Calculons :

$\mathrm{ E = 50 \times 10^6 \times 6,4 \times 10^3 \times 25 \times 10^{-3}}$

$\mathrm{ E = 50 \times 10^6 \times 6,4 \times 10^3 \times 0,025}$

$\mathrm{ E = 8,0 \times 10^9 \, \text{J}}$

2.5. Sachant qu’un foyer consomme une énergie moyenne sur l’année de 4400 kWh, évaluer le nombre de foyers qui pourraient être alimentés pendant 1 an par les orages tombant sur le territoire français. Proposer deux arguments justifiant qu’actuellement la foudre n’est pas exploitée comme source d’énergie électrique.

Calculons l’énergie de tous les orages.

D’après l’énoncé : « Un orage compte en moyenne une centaine de coups de foudre et on dénombre chaque année sur l’ensemble du territoire français de l’ordre de dix mille orages. »

$\mathrm{ E_{\text{total}} = 100 \times 10{000} \times E }$

$\mathrm{E_{\text{total}} = 100 \times 10{000} \times 8,0 \times 10^9}$

$\mathrm{E_{\text{total}} = 8,0 \times 10^{15} \, \text{J}}$

Convertissons cette énergie en kWh.

1 kWh =

1 kWh	3,6 MJ=3,6×10⁶J
E_total	8,0×10¹⁵J

$\mathrm{E_{\text{total}} = \frac{8,0 \times 10^{15}}{3,6 \times 10^6}}$

$\mathrm{E_{\text{total}} = 2,2 \times 10^9 \, \text{kWh}}$

Calcul du nombre de foyers :

1 foyer	4400 kWh
N foyers	2,2×10⁹ kWh

$\mathrm{N = \frac{2,2 \times 10^9}{4400}}$

$\mathrm{N = 5,0 \times 10^5}$

Cinq cent mille foyers pourraient être alimentés pendant 1 an par les orages tombant sur le territoire français.

Arguments justifiant que la foudre n’est pas exploitée comme source d’énergie électrique :

La foudre est un phénomène naturel extrêmement imprévisible et variable. La localisation et le moment où elle frappera sont impossible à prévoir.
La foudre contient une grande quantité d’énergie en un temps très court, nécessitant des équipements capables de résister à des courants extrêmement élevés et des tensions très élevées sans être détruits.

1,0 cm	$4{,}0 \times 10^{-15} \, \text{N}$
x	$8{,}0 \times 10^{-15} \, \text{N}$