Sujet avec enseignement de mathématiques spécifique
Enseignement scientifique première
Durée 1h12 – 12 points – Thème « Son, musique et audition »
Sujet n°ENSSCIMAT165, n°ENSSCIMAT172 , n°ENSSCIMAT173 et n°ENSSCIMAT177
Télécharger l’exercice en PDF :
Les parties 1 et 2 peuvent être traitées indépendamment l’une de l’autre.
La partie 3 est une argumentation s’appuyant sur les parties 1 et 2.
Partie 1 – Masse et fréquence
On dispose de trois marteaux M1, M2 et M3 de masses respectives m1 = 0,24 kg, m2 = 0,48 kg et m3 = 1,44 kg.
L’expérience consiste à les laisser tomber sur une enclume. Un logiciel d’acquisition enregistre le signal sonore émis.
On désigne respectivement par f1, f2 et f3 les fréquences fondamentales des sons émis par les marteaux M1, M2 et M3 lors de l’expérience.
Document 1 – Spectre des fréquences des sons émis lors de la chute des marteaux
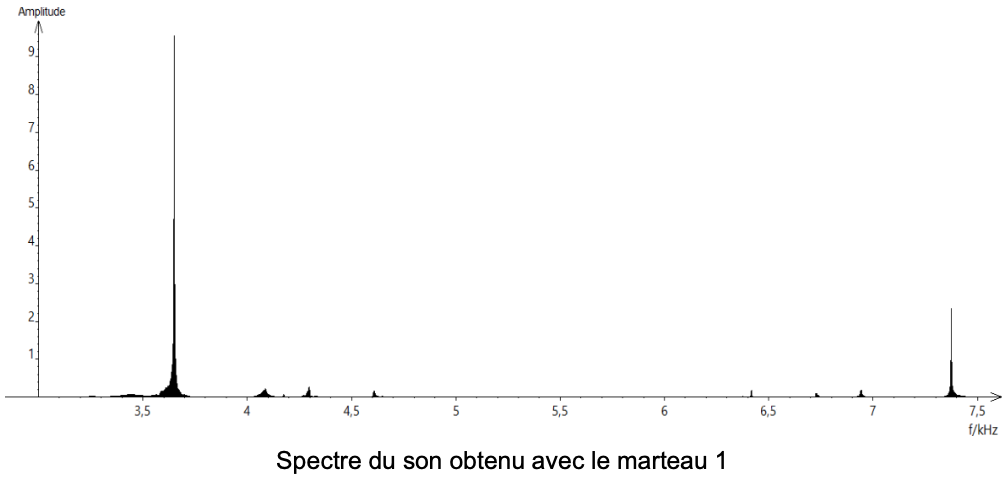

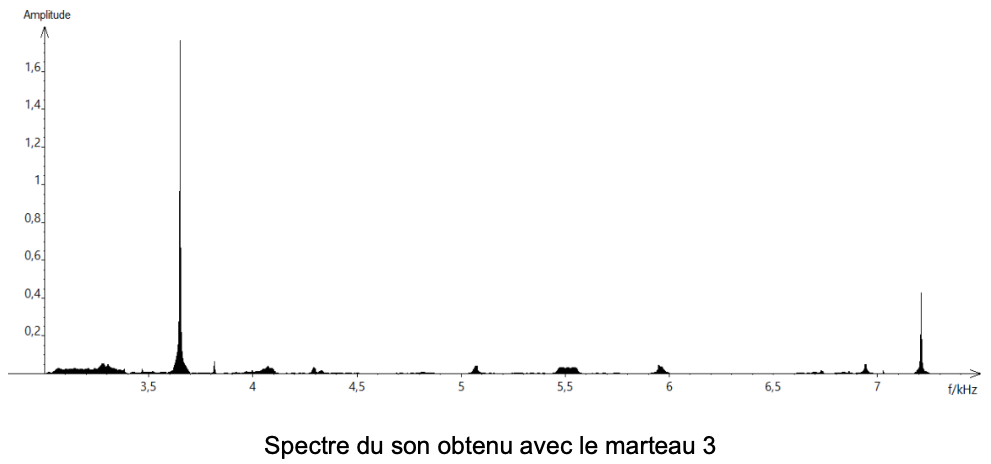
1 – Lire sur le document 1 les fréquences fondamentales f1, f2 et f3 des sons émis lors de l’expérience et noter leurs valeurs sur la copie.
f1= 3,7 kHz
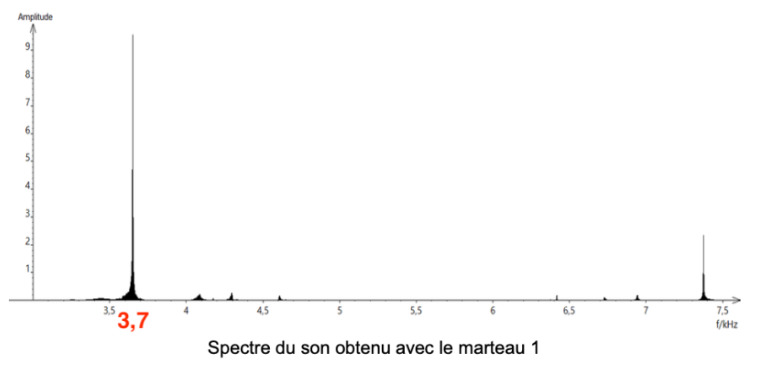
f2 = 3,7 kHz

f3 = 3,7 kHz
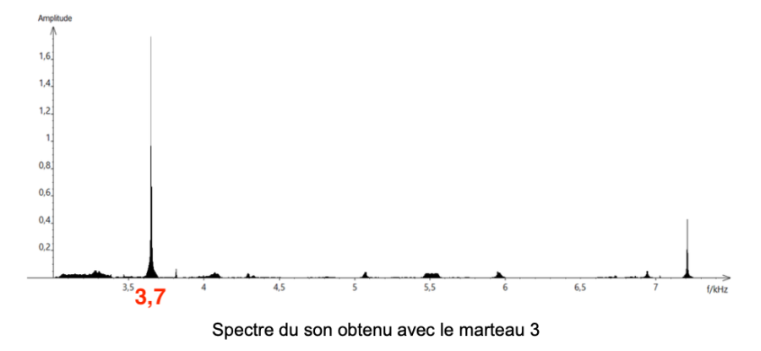
2 – Comparer ces fréquences. La masse du marteau influe-t-elle sur la fréquence fondamentale du son émis ?
Ces fréquences sont identiques.
On en déduit que la masse du marteau n’influe pas sur la fréquence fondamentale du son émis.
3 – Comment qualifie-t-on le son du spectre 2 ? Justifier.
Le son du spectre 2 ne présente qu’un harmonique : c’est un son pur.
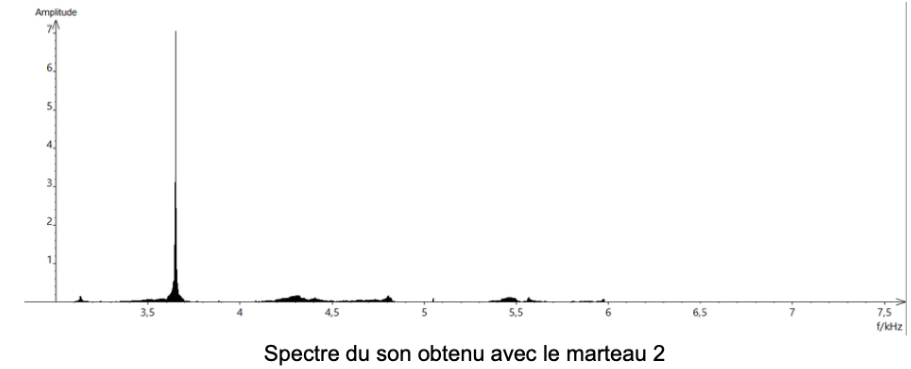
4 – Comment qualifie-t-on le son des spectres 1 et 3 ? Justifier. Comment appelle-t- on la fréquence autre que le fondamental dans ces spectres ?
Les spectres 1 et 3 présentent des sons avec plusieurs harmoniques : ce sont des sont composés.
La fréquence autre que le fondamental dans ces spectres s’appellent les harmoniques.
5 – Grâce à vos connaissances, déterminer si l’humain est capable de détecter les fréquences produites par le marteau 3.
Le marteau 3 produit 2 fréquences 3,7 kHz = 3700 Hz et 7,4 kHz=7400Hz
L’humain est capable de détecter des sons dont les fréquences sont comprises entre 20 et 20 000 Hz.
Ainsi, l’humain est capable de détecter les fréquences produites par le marteau 3.
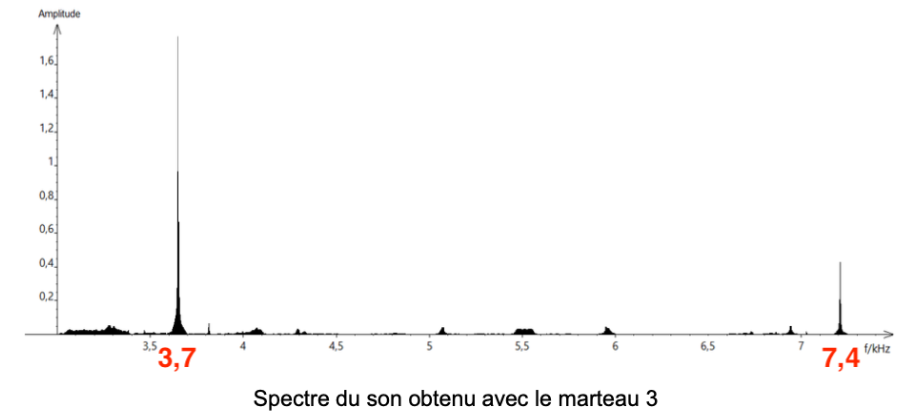
Document 2 – Schéma d’une oreille humaine
Source : www.audition.fr
6 – Présenter comment l’humain parvient à détecter un son. Le document 2 est une aide mais n’a pas pour but d’être analysé.
La vibration de l’air est captée par le pavillon de l’oreille externe. Le son se propage dans le conduit auditif et fait vibrer le tympan.
La vibration du tympan est transmise par les osselets de l’oreille moyenne.
Dans la cochlée, les différentes cellules ciliées sont activées en fonction de la fréquence.
Les cellules ciliées traduisent cette vibration en message nerveux qui est transmis au cerveau par les nerfs auditifs.
Partie 2 – Tension et fréquence
Dans cette partie, on tend une corde de longueur quelconque à l’aide d’une masse variable 𝑚.

On a relevé dans le tableau ci-dessous les fréquences fondamentales obtenues en pinçant la corde :
| Masse (en kg) | 0 | 8,070 | 9,990 | 11,110 |
| Fréquence (en Hz) | 0 | 202 | 224 | 237 |
7 – Peut-on affirmer que la fréquence fondamentale du son est proportionnelle à la masse utilisée pour tendre la corde ? Justifier.
Pour savoir si la fréquence fondamentale du son est proportionnelle à la masse utilisée pour tendre la corde, calculons le rapport f/m :
| Masse (en kg) | 0 | 8,070 | 9,990 | 11,110 |
| Fréquence (en Hz) | 0 | 202 | 224 | 237 |
| Rapport f/m | —– | 25,03 | 22,42 | 21,33 |
Le rapport f/m n’est pas constant.
Ainsi, la fréquence fondamentale du son n’est pas proportionnelle à la masse utilisée pour tendre la corde.
On propose de modéliser le mieux possible la manière dont la fréquence fondamentale, exprimée en Hz, varie en fonction de la masse 𝑚, exprimée en kg, à l’aide d’une fonction définie sur l’ensemble des réels positifs. On considère les trois fonctions suivantes :
𝑓1∶m → $ \sqrt m$ 𝑓2∶m → 25m et 𝑓3∶m→ $\frac{9}{4}m^2$
8 – Donner un tableau de valeurs de chacune des fonctions, en prenant les masses données.
| Masse (en kg) | 0 | 8,070 | 9,990 | 11,110 |
| 𝑓1∶m⟼71√m | 0 | 202 | 224 | 237 |
| Masse (en kg) | 0 | 8,070 | 9,990 | 11,110 |
| 𝑓2∶m⟼25m | 0 | 202 | 250 | 278 |
| Masse (en kg) | 0 | 8,070 | 9,990 | 11,110 |
| 𝑓3∶m⟼9/4 m2 | 0 | 147 | 225 | 278 |
9 – Quelle fonction modélise alors le mieux le problème ? Justifier.
La fonction qui modélise le mieux le problème est f1 car les valeurs correspondent aux valeurs expérimentales.
| Masse (en kg) | 0 | 8,070 | 9,990 | 11,110 |
| Fréquence (en Hz) | 0 | 202 | 224 | 237 |
| Masse (en kg) | 0 | 8,070 | 9,990 | 11,110 |
| 𝑓1∶m⟼71√m | 0 | 202 | 224 | 237 |
Partie 3 – Analyse d’un texte
Voici un extrait du Commentaire au songe de Scipion écrit par Macrobe aux alentours de 400 après JC.
« […] la diversité des sons, indépendante des hommes, correspondait aux marteaux. Alors il mit tout son soin à en évaluer le poids, et après avoir noté la différence de poids qui caractérisait chacun il fit fabriquer des marteaux de poids différents, en plus ou en moins ; les sons produits par leurs coups ne ressemblaient en rien à ceux d’avant et ne s’accordaient plus aussi bien. Il constata alors que l’harmonie sonore était réglée par les poids, et après avoir relevé les nombres qui définissaient la diversité bien accordée de ces poids, il passa des marteaux à l’examen des instruments à cordes : il tendit des boyaux de mouton ou des nerfs de bœuf en y
attachant des poids aussi variés que ceux qu’il avait découverts à propos des marteaux, et il en résulta bien le genre d’accord que lui avait fait espérer son observation antérieure, à laquelle il ne s’était pas livré pour rien. »
Commentaire au songe de Scipion, II, 1, 9-13
10 – En quelques lignes, émettre une critique scientifique détaillée des affirmations contenues dans le Commentaire au songe de Scipion, en vous appuyant sur les résultats obtenus dans les parties 1 et 2.
Dans les questions 1 et 2 on a vu que la masse du marteau n’influe pas sur la fréquence fondamentale du son émis.
Macrobe affirme que le poids des marteaux détermine la hauteur des sons produits, ce qui est incorrect : la fréquence fondamentale du son dépend des propriétés de l’objet frappé, pas de la masse du marteau.
Dans le cas des instruments à cordes, il y attache des poids ce qui modifie la tension des cordes, influençant ainsi la fréquence du son comme vu dans la partie 2.
