Les supercondensateurs

Bac Centres étrangers 2021 Sujet 1

Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 21-PYCJ1G11

[latexpage]

Mots-clés : modèle du condensateur, circuit RC série.

Un supercondensateur permet de stocker et de restituer rapidement de l’énergie électrique.

Dans certains transports en commun, un supercondensateur est utilisé pour emmagasiner un maximum d’énergie électrique en quelques secondes lors des phases de freinage.

Si des condensateurs classiques étaient utilisés à la place des supercondensateurs, il faudrait des armatures de très grandes surfaces et très rapprochées, séparées par un excellent diélectrique.

Cet exercice a pour objectifs :

de comparer qualitativement un supercondensateur avec un condensateur usuel ;
d’étudier le comportement d’un supercondensateur lors de sa charge afin de déterminer expérimentalement la valeur de sa capacité et de la comparer à celle fournie par le fabricant.

Données constructeur sur le supercondensateur étudié :

dimensions : 35 mm × 60 mm
capacité : 400 F
tension maximale : 2,5 V
énergie maximale : 0,35 Wh

1. Comparer la valeur de la capacité du supercondensateur étudié aux valeurs usuelles des capacités des condensateurs utilisées au lycée ou en électronique.

La valeur de la capacité C d’un condensateur plan peut être déterminée à l’aide de la relation :

$C= \epsilon \frac{ S }{d}$

où :

S est la surface en regard des deux armatures,
d est l’écartement entre les deux armatures,
𝜖 est une constante caractéristique du matériau isolant placé entre les deux armatures.

Capacité du supercondensateur : 400 F

Capacités des condensateurs utilisées au lycée ou en électronique : quelques Microfarad

La valeur de la capacité du supercondensateur étudié est très supérieure aux valeurs usuelles des capacités des condensateurs utilisées au lycée ou en électronique

2. Justifier qualitativement les parties en italique et soulignées du texte de présentation des supercondensateurs.

Texte du sujet : « Si des condensateurs classiques étaient utilisés à la place des supercondensateurs, il faudrait des armatures de très grandes surfaces et très rapprochées, séparées par un excellent diélectrique. »

$$C=\epsilon\frac{S}{d}$$

La capacité est proportionnelle à la surface S des armatures, ainsi pour avoir une grande capacité il faut des armatures de très grandes surfaces.

La capacité est inversement proportionnelle à d l’écartement entre les deux armatures, ainsi pour avoir une grande capacité il faut des armatures très rapprochées.

Étude du modèle du circuit RC série

On souhaite déterminer la valeur de la capacité du supercondensateur en utilisant un cycle de charge dans un circuit RC. Pour cela, on étudie dans un premier temps le comportement d’un modèle de circuit RC série.

On considère le circuit électrique schématisé ci-dessous (figure 1) composé d’une source idéale de tension E, d’un interrupteur 𝐾, d’un conducteur ohmique de résistance R, du supercondensateur de capacité C et d’un ampèremètre de résistance interne négligeable (la tension aux bornes de l’ampèremètre est considérée comme nulle).

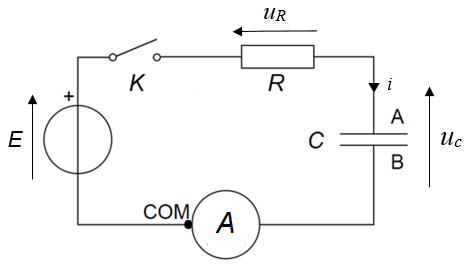
**figure 1**. Circuit électrique RC série

Le supercondensateur est initialement déchargé. À l’instant t = 0 s, on ferme l’interrupteur.

3. Donner la relation entre l’intensité 𝑖(t) du courant électrique et la dérivée de la charge q(t) portée par l’armature A du supercondensateur, puis la relation entre l’intensité 𝑖(t), la capacité C et la dérivée de la tension électrique u_𝐶(t) aux bornes du supercondensateur.

Relation entre l’intensité i(t) du courant électrique et la dérivée de la charge q(t) portée par l’armature A du supercondensateur

$$i(t)=\frac{dq_{(t)}}{dt}$$

Relation entre l’intensité i(t), la capacité C et la dérivée de la tension électrique uC(t) aux bornes du supercondensateur :

La charge q d’un condensateur est proportionnelle à la tension U entre ses armatures :

$$q(t)=C \times U_C(t)$$

D’ou

$$i(t)=\frac{dq(t)}{dt}=\frac{d(CU_C(t))}{dt}=C\frac{dU_C(t)}{dt}$$

4. Montrer que l’équation différentielle dont la tension électrique u_𝐶(t) aux bornes du supercondensateur est une solution est de la forme :

$\frac{d u_C}{dt}(t)+\frac{1}{\tau} u_C(t)=\frac{E}{\tau} $

Exprimer la constante de temps 𝜏 en fonction de R et de C.

Réponse :

D’après la loi d’additivité des tensions ou loi des mailles :

$E=U_C(t)+U_R(t)$

Or $U_R(t)=R \times i$

$E=U_C(t)+R \times i$

Or $ i(t)=\frac{dq(t)}{dt}$

$E=U_C(t)+R \times \frac{dq(t)}{dt}$

Or $q(t)=C \times U_C(t)$

$E=U_C(t)+R \times \frac{C \times U_C(t)}{dt}$

$E=U_C(t)+RC \times \frac{U_C(t)}{dt}$

Par identification avec la forme recherchée :

$$\frac{dU_C(t)}{dt}+\frac{1}{\tau}U_C(t)=\frac{E}{\tau}$$

$$\tau=RC$$

5. Vérifier que les solutions de cette équation différentielle sont de la forme :

$u_C(t)=A e^{-\frac{t}{\tau}}+E $

Déterminer l’expression de A pour la situation étudiée.

Vérifions que les solutions de cette équation différentielle sont de la forme :

$$U_C\left(t\right)=Ae^{-\frac{t}{\tau}}+E$$

-Dérivons $U_C\left(t\right)$ :

$$\frac{dU_C(t)}{dt}=-\frac{A}{\tau}e^{-\frac{t}{\tau}}$$

-Remplaçons $U_C\left(t\right)$ et $\frac{dU_C(t)}{dt}$ dans l’équation :

$$\frac{dU_C(t)}{dt}+\frac{1}{\tau}U_C(t)=\frac{E}{\tau}$$

$$-\frac{A}{\tau}e^{-\frac{t}{\tau}}+\frac{1}{\tau}(Ae^{-\frac{t}{\tau}}+E)=\frac{E}{\tau}$$

$$-\frac{A}{\tau}e^{-\frac{t}{\tau}}+\frac{1}{\tau}Ae^{-\frac{t}{\tau}}+\frac{1}{\tau}E=\frac{E}{\tau}$$

$$\frac{1}{\tau}E=\frac{E}{\tau}$$

E=E

La solution de la forme $U_C\left(t\right)=Ae^{-\frac{t}{\tau}}+E$ vérifie l’équation différentielle.

Or cette relation est vraie quelque soit le temps, donc :

$$U_C\left(t=0\right)=0$$

$$Ae^{-\frac{0}{\tau}}+E=0$$

A+E=0

A=-E

Soit $U_C\left(t\right)=-Ee^{-\frac{t}{\tau}}+E$

$$U_C\left(t\right)=E(1-e^{-\frac{t}{\tau}})$$

Etude expérimentale et détermination de la valeur de la capacité

On réalise le montage précédent avec une source idéale de tension de valeur E = 2,5 V et un conducteur ohmique de résistance R = 2,0 Ω .

À l’aide d’une carte d’acquisition, on réalise le suivi temporel de la tension aux bornes du supercondensateur durant sa charge (figure 2 page 10/15).

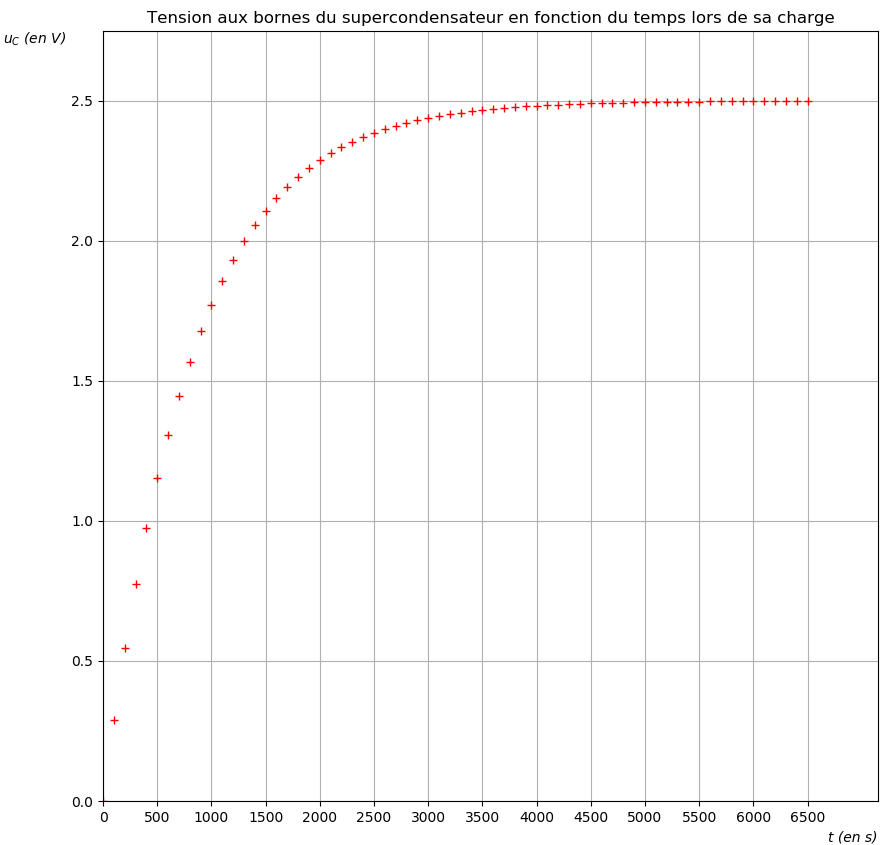
6. Déterminer la valeur C₁ de la capacité du supercondensateur en explicitant la démarche suivie.

La constante de temps \tau=RC , peut être déterminée graphiquement par deux méthodes :

$$U_C\left(t=\tau\right)=E\left(1-e^{-\frac{\tau}{\tau}}\right)$$

$$U_C\left(t=\tau\right)=E\left(1-e^{-1}\right)$$

$$U_C\left(t=\tau\right)0,63E$$

On lit le temps pour lequel $$U_C\left(\tau\right)=0,63E=0,63 \times 2,5=1,6\ V$$

On trace la tangente à la courbe à t=0 et on regarde l’abscisse du point d’intersection entre cette tangente et l’asymptote $U_C=E$ pour la charge, et $U_C=0$ pour la décharge.

On trouve $\tau=800\ s$

$$C_1=\frac{\tau}{R}$$

$$C_1=\frac{800}{2,0}=4,0.{10}^2F$$

À l’aide d’un microcontrôleur et d’un programme en python, on peut reproduire l’expérience un grand nombre de fois pour affiner la détermination du temps caractéristique du dipôle RC réalisé avec ce même supercondensateur. Ce programme permet d’obtenir le temps caractéristique du dipôle RC en déterminant la date pour laquelle le condensateur est chargé à 63%.

Après 10 exécutions successives du programme, on obtient, pour le temps caractéristique du dipôle RC, la série de valeurs suivantes exprimées en ms :

811614

818076

810301

810495

818526

812067

811327

813109

817838

819474

La moyenne $\bar{\tau_2}$ de la série de mesures est $\bar{\tau_2}= 814,2827 s$.

La calculatrice donne 1,175 s pour le calcul de l’incertitude-type.

7. Écrire de manière appropriée le résultat de la mesure du temps caractéristique avec son incertitude-type.

L’incertitude porte sur le chiffre des unités. Ainsi, tau ne peut être plus précis que le chiffre des unités.

On majore le résultat de l’incertitude :

$$\mathbf{\tau}=\mathbf{814}\pm\mathbf{2}\ \mathbf{s}$$

On estime que l’incertitude-type de la résistance du conducteur ohmique est u(R) = 0,1 Ω.

L’incertitude-type sur la valeur de la capacité C₂ du supercondensateur se déduit des mesures de la résistance et du temps caractéristique moyen par la relation :

$u(C_2)= C_2 \sqrt{\left (\frac{u(R)}{R}\right)^2+\left (\frac{u(\overline{\tau_2})}{\overline{\tau_2}}\right)^2$

8. Déterminer la valeur de la capacité C₂ du supercondensateur ainsi que son incertitude-type.

Calculons la capacité $C_2$ :

$$C_2=\frac{\tau_2}{R}$$

$$C_2=\frac{814}{2,0}=4,1.{10}^2\ F$$

Calculons l’incertitude-type $u(C_2)$ :

$$\mathbf{u}(\mathbf{C}_\mathbf{2})=\mathbf{C}_\mathbf{2}\sqrt{\left(\frac{\mathbf{u}(\mathbf{R})}{\mathbf{R}}\right)^\mathbf{2}+\left(\frac{\mathbf{u}(\bar{\mathbf{\tau}_\mathbf{2}})}{\bar{\mathbf{\tau}_\mathbf{2}}}\right)^\mathbf{2}}$$

$$\mathbf{u}(\mathbf{C}_\mathbf{2})=\mathbf{4},\mathbf{1}.{\mathbf{10}}^\mathbf{2}\sqrt{\left(\frac{\mathbf{0},\mathbf{1}}{\mathbf{2},\mathbf{0}}\right)^\mathbf{2}+\left(\frac{\mathbf{2}\ }{\mathbf{814}\ }\right)^\mathbf{2}}$$

$$\mathbf{u}(\mathbf{C}_\mathbf{2})=\mathbf{2}.{\mathbf{10}}^\mathbf{1}\mathbf{F}$$

Exprimons la capacité $C_2$ avec son incertitude-type:

$$C_2=4,1.{10}^2\pm2.{10}^1$$

$$C_2=(4,1\pm0,2).{10}^2F$$

9. Comparer la valeur de la capacité C₂ mesurée expérimentalement avec la valeur de référence C_ref donnée par le constructeur en utilisant le quotient $\frac{\lvert C_2-C_{ref} \rvert}{u(C_2)}$ . Conclure.

$$\frac{\left|\mathbf{C}_\mathbf{2}{-\mathbf{C}}_{\mathbf{ref}}\right|}{\mathbf{u}(\mathbf{C}_\mathbf{2})}=\frac{\left|\mathbf{4},\mathbf{1}.{\mathbf{10}}^\mathbf{2}-\mathbf{400}\right|}{\mathbf{2}.{\mathbf{10}}^\mathbf{1}}=\mathbf{0},\mathbf{5}<\mathbf{2}$$

La valeur mesurée est en accord avec la valeur de référence.