ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée
Sujet 2024 n°SPEPHCH106 et n°SPEPHCH114
[latexpage]
Inventée dans les années 70 par la NASA pour la manipulation d’échantillons liquides sans contact physique, la lévitation acoustique vise à suspendre des objets dans un milieu en utilisant des ondes sonores, comme s’ils étaient maintenus par des doigts invisibles. Cette technique a des applications intéressantes, par exemple pour l’obtention de nouveaux matériaux pour l’électronique ou pour la synthèse de médicaments.
La lévitation acoustique de deux boules de polystyrène peut être réalisée au laboratoire en utilisant deux émetteurs à ultrasons.
Placés verticalement en vis-à-vis, ils émettent deux ondes ultrasonores de même longueur d’onde dont la superposition génère des zones horizontales de surpression de l’air, appelées « ventres », alternant avec des zones de dépression, appelées « nœuds ».
C’est au niveau de ces « nœuds » que les objets peuvent rester en suspension.

Données :
- extrait de la fiche technique des émetteurs à ultrasons :
- émetteur à ultrasons 40 kHz ;
- tension maximale : 50 Vpp ;
- pression acoustique : > 110 dB @ 10 V – 30 cm ;
- température d’utilisation : – 20°C à + 70°C ;
- dimensions : diamètre 10 mm ; hauteur 7 mm ;
- volume d’une sphère de rayon R : $V=\frac{4}{3}\pi R^3$;
- intensité du champ de pesanteur terrestre : g = 9,81 m.s-2 ;
- célérité du son dans l’air dans les conditions de l’expérience : c = 343 m.s-1 ;
- masse volumique du polystyrène expansé : ρ = 20 kg.m-3.
1. Étude de l’onde ultrasonore émise par un émetteur
Une onde sonore correspond à la propagation dans un milieu matériel, le plus souvent l’air, d’une surpression produite de manière périodique par la vibration d’une membrane de haut- parleur par exemple.
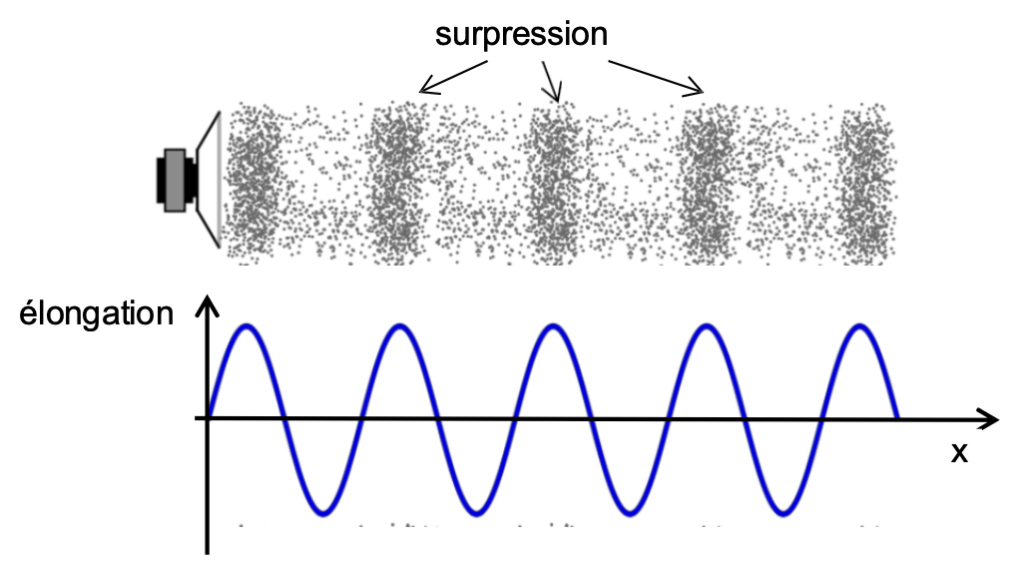
D’après https://commons.wikimedia.org
1.1. Proposer deux adjectifs pour caractériser l’onde sonore représentée ci-dessus et préciser la nature de la grandeur physique associée à l’élongation de cette onde.
L’onde sonore représentée est longitudinale (la perturbation se produit dans la même direction que la propagation) et périodique (la perturbation qui la caractérise se répète à intervalles de temps réguliers).
La grandeur physique associée à l’élongation de cette onde est l’amplitude.
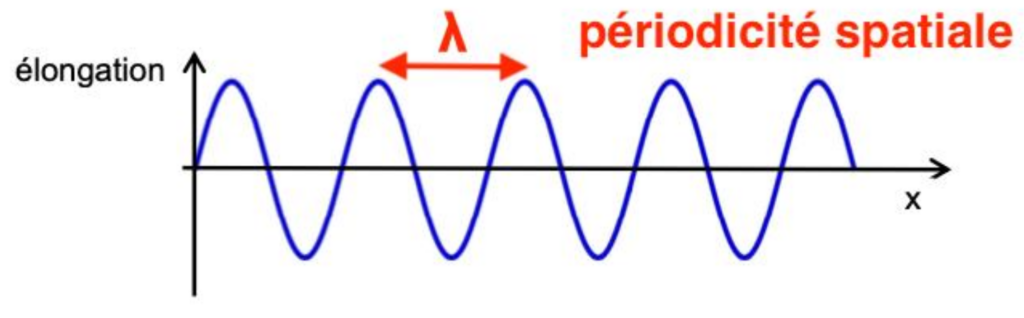
1.2. Cette onde présente une « périodicité spatiale ».
1.2.1. Expliquer l’expression « périodicité spatiale ».
La période spatiale, appelée longueur d’onde, est égale à la distance minimale pour laquelle l’onde se répète identique à elle-même.
1.2.2. Recopier l’allure de la courbe représentée ci-dessus, donnant l’élongation en fonction de la distance x à une date t0 donnée, en précisant la grandeur caractéristique associée à cette périodicité spatiale.
La période spatiale, appelée longueur d’onde, est égale à la distance minimale pour laquelle l’onde se répète identique à elle-même.
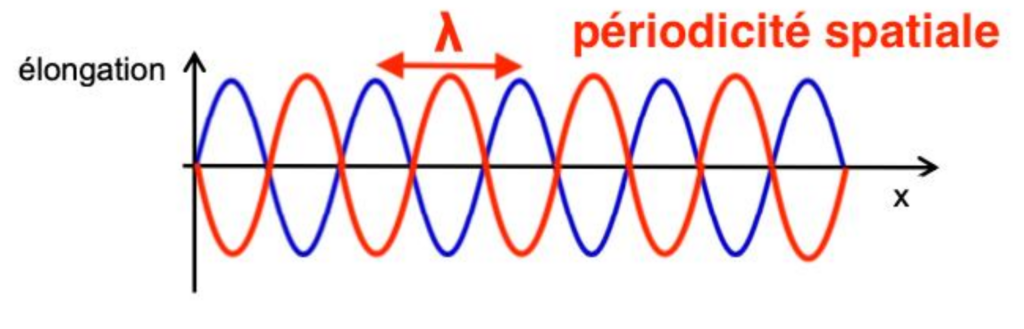
1.2.3.On note T la période temporelle de l’onde sonore. Donner, en justifiant, l’allure de la courbe donnant l’élongation en fonction de la distance x à la date $t_0+\frac{T}{2}$.
A chaque période temporelle T, l’onde se déplace d’une longueur d’onde λ. Pour T/2, elle se déplace d’une demi longueur d’onde λ/2.
L’allure de la courbe donnant l’élongation en fonction de la distance x à la date t0 + T/2 est donné ci-dessous en rouge :
1.3. Pourquoi utilise-t-on le terme « ultrasonore » pour l’onde émise par les émetteurs utilisés pour l’expérience de lévitation acoustique réalisée au laboratoire ?
On utilise le terme « ultrasonore » pour l’onde émise par les émetteurs utilisés pour l’expérience de lévitation acoustique réalisée au laboratoire car la fréquence utilisée 40 kHz est supérieure à 20 kHz et appartient donc aux ultrasons.
2. Analyse de l’expérience de lévitation acoustique.
2.1. On peut établir que les nœuds où les billes de polystyrène peuvent léviter sont distants de $\frac{\lambda }{2}$ , λ étant la longueur d’onde des ondes ultrasonores utilisées.
2.1.1. En utilisant la photo de l’expérience donnée en début de sujet et les caractéristiques géométriques des émetteurs, estimer la valeur de la longueur d’onde des ondes ultrasonores utilisées.
La fiche technique des émetteurs à ultrasons : hauteur 7 mm ;
| Schéma | Réel |
| 1 cm | 7 mm |
| 0,7 cm | $\frac{\lambda }{2}$ |
\[ \mathrm{ \frac{\lambda}{2} = \frac{0,7 \times 7}{1}}\]
\[ \mathrm{ \frac{\lambda}{2} = 4,9 \, \text{mm}}\]
\[ \mathrm{ \lambda = 2 \times 4,9}\]
\[ \mathrm{ \lambda = 9,8 \, \text{mm}}\]

2.1.2. Rappeler la relation entre longueur d’onde λ, fréquence f et célérité c du son dans l’air.
c=λ×f
2.1.3. Le résultat obtenu à la question 2.1.1 est-il compatible avec la valeur de la fréquence des ondes donnée par le constructeur ? Argumenter la réponse.
\[ \mathrm{ c = \lambda \times f}\]
\[ \mathrm{ f = \frac{c}{\lambda}}\]
\[ \mathrm{ f = \frac{343}{9,8 \times 10^{-3}}}\]
\[ \mathrm{ f = 3,5 \times 10^4 \, \text{Hz}}\]
\[ \mathrm{ f = 35 \, \text{kHz}}\]
D’après la fiche technique des émetteurs à ultrasons : les émetteurs à ultrasons émettent à 40 kHz. Notre résultat est du même ordre de grandeur que celui trouvé. La différence vient du fait que la mesure sur le schéma est imprécise.
Ainsi, Le résultat obtenu à la question 2.1.1 est-il compatible avec la valeur de la fréquence des ondes donnée par le constructeur.
2.2. Le diamètre d’une bille de polystyrène peut être estimé à 2,5 mm.
2.2.1. Vérifier que la masse m de la bille est de l’ordre de 0,16 mg.
\[ \mathrm{ \rho = \frac{m}{V}}\]
\[ \mathrm{ \frac{m}{V} = \rho}\]
\[ \mathrm{ m = \rho \times V}\]
Or
\[ \mathrm{ V = \frac{4}{3} \pi R^3}\]
D’où
\[ \mathrm{ m = \rho \times \frac{4}{3} \pi R^3}\]
\[ \mathrm{ m = 20 \times \frac{4}{3} \pi \left(\frac{2,5 \times 10^{-3}}{2}\right)^3}\]
\[ \mathrm{ m = 20 \times \frac{4}{3} \pi \left(1,25 \times 10^{-3}\right)^3}\]
\[ \mathrm{ m = 20 \times \frac{4}{3} \pi \times 1,953125 \times 10^{-9}}\]
\[ \mathrm{ m = 20 \times 8,18 \times 10^{-9}}\]
\[ \mathrm{ m = 1,6 \times 10^{-7} \, \text{kg}}\]
\[ \mathrm{ m = 1,6 \times 10^{-7} \times 10^3 \, \text{g}}\]
\[ \mathrm{ m = 1,6 \times 10^{-4} \, \text{g}}\]
\[ \mathrm{ m = 0,16 \times 10^{-3} \, \text{g}}\]
\[ \mathrm{ m = 0,16 \, \text{mg}}\]
Ainsi, la masse m de la bille a pour valeur 0,16 mg.
2.2.2. Déterminer la valeur de la force exercée par l’air sur chaque bille.
Chaque bille est en lévitation. Elle est en équilibre : d’après la première loi de Newton, les forces se compensent :
\[ \mathrm{ \sum \overrightarrow{F}_{\text{ext}} = 0}\]
\[ \mathrm{ \overrightarrow{P} + \overrightarrow{F}_{\text{air}} = 0}\]
\[ \mathrm{ \overrightarrow{F}_{\text{air}} = -\overrightarrow{P}}\]
Remarque : le signe négatif indique que les deux forces ont des sens opposés. Elles ont la même norme (même valeur).
\[ \mathrm{ \overrightarrow{F}_{\text{air}} = \overrightarrow{P}}\]
Or
\[ \mathrm{ \overrightarrow{P} = m \times g}\]
D’où
\[ \mathrm{ \overrightarrow{F}_{\text{air}} = m \times g}\]
\[ \mathrm{ \overrightarrow{F}_{\text{air}} = 1{,}6 \times 10^{-6} \text{ N}}\]
2.2.3. Dans une approche simplifiée, on cherche à expliquer la lévitation de la bille de polystyrène par l’existence de la force $\overrightarrow{F_A}$ exercée sur tout corps immergé dans un fluide de la part de celui-ci, appelée poussée d’Archimède, verticale, dirigée de bas en haut et dont l’expression de la norme FA est donnée par :
\[ \mathrm{F_A=\rho _{fluide}Vg}\]
où ρfluide est la masse volumique du fluide, V le volume du corps immergé et g l’intensité de la pesanteur.
a) Que peut-on alors dire des masses volumiques de l’air et du polystyrène ?
\[ \mathrm{ F_A = \rho_{\text{fluide}} \times V \times g}\]
\[ \mathrm{ F_A = \rho_{\text{air}} \times V \times g}\]
\[ \mathrm{ P = m \times g}\]
Or
\[ \mathrm{ \rho = \frac{m}{V}}\]
\[ \mathrm{ \frac{m}{V} = \rho}\]
\[ \mathrm{ m = \rho \times V}\]
D’où
\[ \mathrm{ P = \rho_{\text{poly}} \times V \times g}\]
Pour qu’il y ait lévitation, il faut que
\[ \mathrm{ F_A = P}\]
\[ \mathrm{ \rho_{\text{air}} \times V \times g = \rho_{\text{poly}} \times V \times g}\]
\[ \mathrm{ \rho_{\text{air}} = \rho_{\text{poly}}}\]
Ainsi, pour qu’il y ait lévitation, il faut que les masses volumiques de l’air et du polystyrène soient égales.
b) Critiquer cette approche sachant que la valeur de la masse volumique de l’air à 20 °C est 1,2 kg.m-3.
– Masse volumique de l’air à 20 °C : \( \rho_{\text{air}} = 1{,}2 \text{ kg/m}^3 \)
– Masse volumique du polystyrène expansé : \( \rho_{\text{poly}} = 20 \text{ kg/m}^3 \)
\[ \mathrm{ \rho_{\text{air}} < \rho_{\text{poly}}}\]
Contrairement au résultat trouvé à la question précédente : la lévitation ne peut pas s’expliquer uniquement par la poussée d’Archimède.
