L’homme canon

Bac Liban 2024 Sujet 1

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°24-PYCJ1G11

Sujet et corrigé

EXERCICE 3 : L’homme canon (5 points)

Dans le cirque traditionnel américain, la famille Smith est célèbre pour ses numéros d’homme canon, qui consistent à éjecter d’un canon modifié une personne dûment bottée et casquée. L’artiste n’est pas propulsé comme un boulet par de la poudre à canon, mais par un ressort ou un jet d’air comprimé. L’homme- canon atterrit ordinairement sur un filet horizontal ou un matelas pneumatique, dont l’emplacement est déterminé par le calcul, puis validé par des essais avec des mannequins. Les dispositifs de sécurité ne mesurent généralement pas plus de 15 mètres sur 7, une taille extrêmement réduite lorsque l’on prend en compte la longueur moyenne de leur vol.

Stéphanie Smith, femme-canon au Royal Melbourne Show en 2005.

Lors d’un vol à Kennywood en 1998, David Smith Jr a homologué un premier saut « record » de portée 56,64 m. La portée correspond à la distance parcourue sur l’axe horizontal entre l’instant initial et l’instant où l’homme-canon arrive dans le filet horizontal.

On étudiera le mouvement de l’homme-canon dans le référentiel terrestre supposé galiléen.

Pendant son vol, on considère que le système {artiste + équipement} , assimilé à un point matériel, noté G, de masse totale m = 80 kg, n’est soumis qu’à son poids $\overrightarrow{P}$, devant lequel toute action de l’air est négligée. A la date t = 0 s, l’homme-canon démarre son vol et occupe alors la position G₀. Après le vol, le système retrouve le contact avec le filet de protection situé à une hauteur h = 8,0 m au-dessus du sol. La situation est schématisée ci-dessous.

Ce vol a été réalisé dans les conditions suivantes :

• Canon incliné de α = 45° par rapport à l’horizontale ;
• Vitesse d’éjection initiale V₀ = 31 m∙s^-1 ;
• Bouche de sortie du canon située à H = 8,0 m au-dessus du sol.

Données : intensité de la pesanteur g = 9,81m∙s^-2

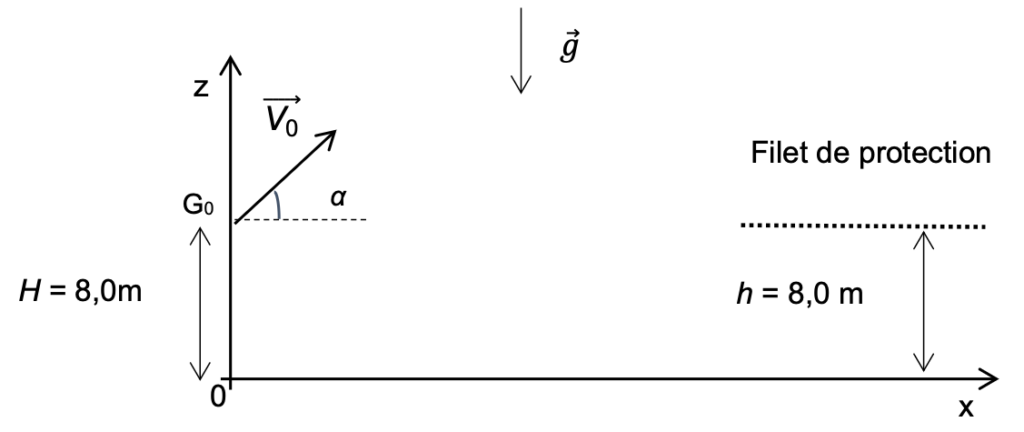
Schéma de la situation

1.    Étude énergétique du vol de l’homme canon

Q.1. Exprimer l’énergie mécanique du système à la date t = 0 en fonction de sa masse m, de l’altitude H et de sa vitesse initiale V₀.

$E_m=E_c+E_{pp}$
$$E_m=\frac{1}{2}\times m\times v^2+m\times g\times z$$

A la date $t=0s$ :
$$E_m(0)=\frac{1}{2}\times m\times v_0^2+m\times g\times z_0$$
$$E_m(0)=\frac{1}{2}\times m\times v_0^2+m\times g\times H$$

Q.2. À l’aide d’un raisonnement énergétique, déterminer la vitesse du système à l’arrivée dans le filet.

D’après le sujet, le système n’est soumis qu’a son poids. Ainsi l’énergie mécanique se conserve :
$E_m\left(filet\right)=E_m(0)$
$$\frac{1}{2}\times m\times v_{filet}^2+m\times g\times z_{filet}=\frac{1}{2}\times m\times v_0^2+m\times g\times H$$
$$\frac{1}{2}\times m\times v_{filet}^2+m\times g\times h=\frac{1}{2}\times m\times v_0^2+m\times g\times H$$
$$\frac{1}{2}\times v_{filet}^2+g\times h=\frac{1}{2}\times v_0^2+g\times H$$
$$\frac{1}{2}\times v_{filet}^2=\frac{1}{2}\times v_0^2+g\times H-g\times h$$
$$\frac{1}{2}\times v_{filet}^2=\frac{1}{2}\times v_0^2+g\times \left(H-h\right)$$
$$v_{filet}^2=v_0^2+2\times g\times \left(H-h\right)$$
$$v_{filet}=\sqrt{v_0^2+2\times g\times \left(H-h\right)}$$
$$v_{filet}=\sqrt{{31}^2+2\times 9,81\times \left(8-8\right)}$$
$$v_{filet}=31\ m.s^{-1}$$

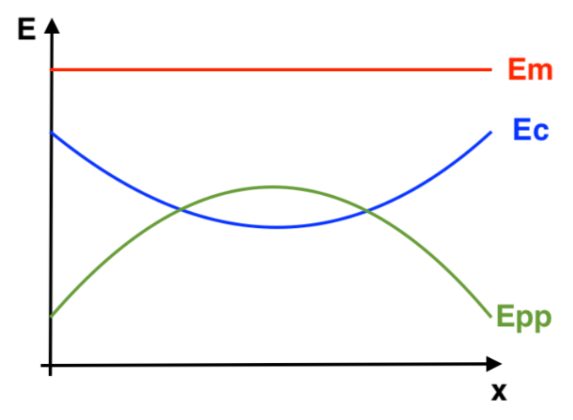
Q.3. Représenter sur votre copie, sans souci d’échelle, l’évolution des énergies cinétique, potentielle de pesanteur et mécanique au cours du vol.

2.    Étude du mouvement de l’homme canon après le lancer

Q.4. En appliquant la deuxième loi de Newton au système, exprimer les coordonnées du vecteur accélération du système pendant le vol.

Système {artiste + équipement}
Référentiel terrestre supposé galiléen

D’après la deuxième loi de newton :
$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$
$\overrightarrow{P}=m\overrightarrow{a}$
$m\overrightarrow{g}=m\overrightarrow{a}$
$\overrightarrow{g}=\overrightarrow{a}$

Or

$$\overrightarrow{g}\begin{pmatrix}0 \\ -g\end{pmatrix}$$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.

$$\overrightarrow{a}\begin{pmatrix}a_x(t)=0 \\ a_z(t)=-g\end{pmatrix}$$

Q.5. En déduire que les équations horaires de son mouvement pendant le vol sont :

$$\overrightarrow{OG}\begin{cases}
x(t)=V_0\times\cos(\alpha)\times t\\
z(t)=-\frac{1}{2}\times g\times t^2+V_0\times\sin(\alpha)\times t+H
\end{cases}$$

$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$
On intègre le système d’équation précédent :
$$\overrightarrow{v}\begin{pmatrix}v_x(t)=C_1\\v_z(t)=-g t+C_2\end{pmatrix}$$
Pour trouver les constantes, on utilise ${\overrightarrow{v}}_0$
$$ {\overrightarrow{v}}0\begin{pmatrix}v_{0x}=v_0\ cos\alpha\\v_{0z}=v_0\ sin \alpha\end{pmatrix}$$
d’ou
$$\overrightarrow{v}\begin{pmatrix}v_{x(t)}=v_0\ cos\alpha\\{\ v}_{z\left(t\right)}=-g t+v_0\ sin\ \alpha\end{pmatrix}$$
$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$

On intègre le système d’équation précédent :
$$\overrightarrow{OG}\begin{pmatrix}x\left(t\right)=\ \ v_0\cos(\alpha)\times t\ +C_3\\z\left(t\right)=-\frac{1}{2}g t^2+v_0\sin(\alpha)\times t\ +C_4 \end{pmatrix}.$$
Pour trouver les constantes, on utilise ${\overrightarrow{OG}}_0$
$$ {\overrightarrow{OG}}_0\ \begin{pmatrix}x_0=0\\z_0=H \end{pmatrix}$$
d’ou

$$\overrightarrow{OG}\begin{pmatrix}x\left(t\right)=\ \ v_0\cos(\alpha)\times t\\ z\left(t\right)=-\frac{1}{2}g t^2+v_0\sin{\left(\alpha\right)}\times t+H \end{pmatrix}$$

Q.6. Donner la valeur de la coordonnée z(t) lorsque le système entre en contact avec le filet de protection.

Graphiquement : $z_{filet}=h=8,0\ m$

Q.7. En déduire la valeur de la durée t_V du vol, puis celle de la longueur x_V de la portée.

La durée $t_v$ est la durée nécessaire pour que le système atteigne le filet.
$$z\left(t_v\right)=-\frac{1}{2}g t_v^2+v_0\sin{\left(\alpha\right)}\times t_v+H$$
$$h=-\frac{1}{2}g t_v^2+v_0\sin{\left(\alpha\right)}\times t_v+H$$
$$h-H=-\frac{1}{2}g t_v^2+v_0\sin{\left(\alpha\right)}\times t_v$$
$$0=\left(-\frac{1}{2}g t_v+v_0\sin{\left(\alpha\right)}\right)\times t_v$$
Un produit de facteur est nul si et seulement si un de ses facteur est nul :
$t_v=0\ s$ qui correspond au temps du départ
$$-\frac{1}{2}g t_v+v_0\sin{\left(\alpha\right)}=0$$
$$-\frac{1}{2}g t_v=-v_0\sin{\left(\alpha\right)}$$
$$t_v=\frac{2\times v_0\sin{\left(\alpha\right)}}{g}$$
$$t_v=\frac{2\times 31\times \sin{\left(45\right)}}{9,81}$$
$$t_v=4,5\ s$$

Déterminons $x_v$ :
$$x_v=\ \ v_0\cos(\alpha)\times t_v$$
$$x_v=\ \ 31\times \cos(45)\times 4,5$$
$$x_v=\ \ 99\ m$$

Q.8. Comparer la longueur estimée par ce modèle avec la longueur du record homologué ce jour-là de 56,64 m. Déterminer si le modèle de la chute libre est adapté à la description du vol. Proposer une explication.

La valeur trouvée est bien supérieure à la valeur expérimentale. Ainsi, le modèle de la chute libre n’est pas adapté à la description du vol. Il faut prendre en compte les forces de frottements.