L’installation de l’homme sur la lune

Bac Polynésie 2021 Sujet 2

Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 21-PYCJ1PO1

Mots-clés : Satellite, repère de Frenet, chute libre.

Le programme Artemis est un programme spatial habité de la NASA, l’agence spatiale américaine, dont l’objectif est d’amener un équipage sur le sol lunaire d’ici 2024.

Celui-ci doit déboucher sur une exploration durable sous la forme de l’installation d’un poste permanent sur la Lune. Source : Wikipédia

La partie A s’intéressera à la mise en place d’un satellite de télécommunication autour de la Lune et la partie B analysera l’alunissage d’un module lunaire.

A- Étude d’un satellite de télécommunication

L’étude ne portera que sur un seul satellite dont l’orbite autour de la Lune sera considérée comme circulaire. On négligera l’influence de la Terre sur le mouvement du satellite.

*Source :* *http://education.meteofrance.fr/*

Analogie avec les satellites terrestres

« L’orbite des satellites géostationnaires se trouve dans le plan équatorial de la Terre à une altitude de près de 36 000 km. De ce fait, ils tournent à la même vitesse angulaire que la Terre. Ils sont donc fixes par rapport à un observateur situé sur la Terre et voient ainsi toujours le même disque terrestre. »

Données :

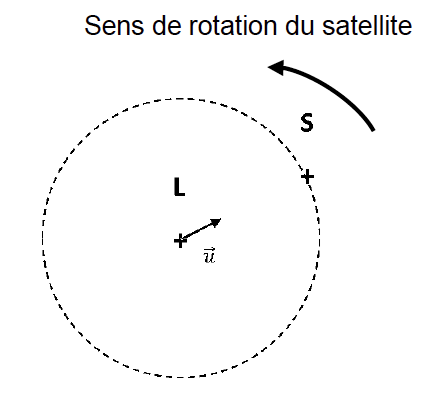
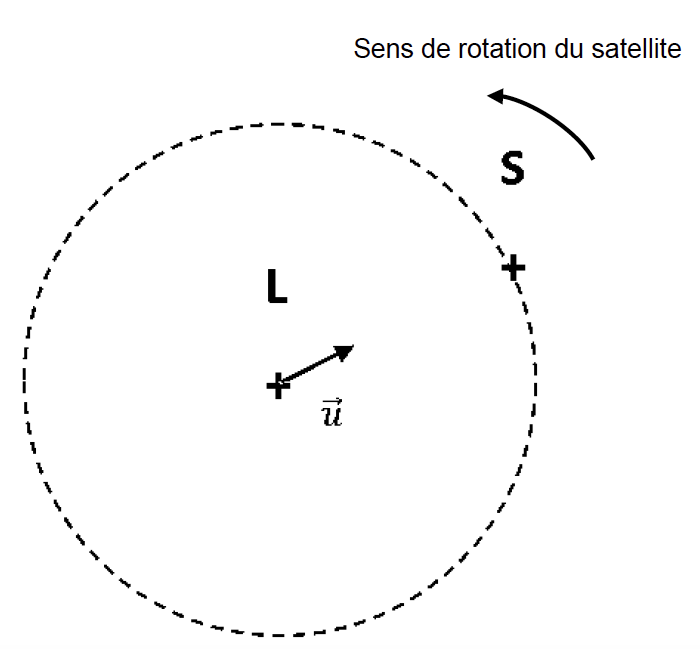
Trajectoire circulaire du centre du satellite (S) autour du centre de la Lune (L) $\overrightarrow{u}$ est le vecteur unitaire orienté de L vers S

Force d’interaction gravitationnelle entre un objet A de masse M_A et un objet B de masse M_B distants de d_AB

$\overrightarrow{F}_{A/B}=-\overrightarrow{F}_{B/A} =\frac{G \times M_A \times M_B}{d_{AB}^2} \cdot \overrightarrow{u}_{A/B}$

Le vecteur unitaire $\overrightarrow{u}_{A/B}$ est orienté de A vers B.

1. Proposer une définition de ce que pourrait être un satellite lunostationnaire en comparant sa période de révolution autour de la Lune à la période de rotation de la Lune sur elle- même.

Réponse :

Un satellite lunostationnaire est un satellite qui est fixe par rapport à un observateur placé sur la lune. Sa période de révolution doit être exactement la même que la période de rotation la de la lune sur elle même.

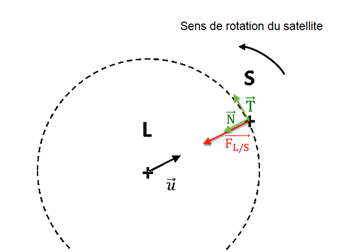
2. Représenter la force d’interaction gravitationnelle $\overrightarrow{F}_{L/S}$ exercée par la Lune sur ce satellite sans souci d’échelle sur le document réponse à rendre avec la copie.

Réponse :

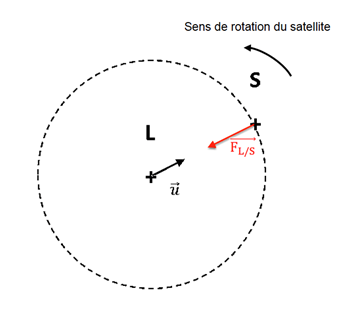
3. Établir l’expression de cette force $\overrightarrow{F}_{L/S}$ en fonction de G, M_S, M_L, d_LS et $\overrightarrow{u}$ .

Réponse :

$\overrightarrow{F}_{L/S}=-G\times \frac{M_{S}\times M_{L}}{d_{LS}^2}\overrightarrow{u}$

Description du mouvement du satellite

Données :

Période de rotation de la lune sur elle-même : T = 27,3 jours
Constante de gravitation universelle : G = 6,67 × 10^–11 N·m²·kg^–2
Masse de la Lune : M_L = 7,34 × 10²² kg
Rayon de la Lune : R_L = 1,74 × 10⁶ m
Périmètre d’un cercle : P = 2πR

4. À l’aide de la deuxième loi de Newton, établir l’expression du vecteur accélération $\overrightarrow{a}_G$ du centre du satellite en fonction de G, M_S, M_L, d_LS et $\overrightarrow{u}$ .

Réponse :

Système : ISS

Référentiel : Géocentrique supposé galiléen

D’après la 2^nd loi de Newton :

$\sum_{}^{}\overrightarrow{F_{ext}}=M_{S}\overrightarrow{a_{G}}$

$\overrightarrow{F}_{L/S}=M_{S}\overrightarrow{a_{G}}$

$-G\times \frac{M_{S}\times M_{L}}{d_{LS}^2}\overrightarrow{u}=M_{S}\overrightarrow{a}}$

$\overrightarrow{a}=-G\times \frac{M_{L}}{d_{LS}^2}\overrightarrow{u}$

5. Représenter le vecteur unitaire tangentiel $\overrightarrow{T}$ et le vecteur unitaire normal $\overrightarrow{N}$ du repère de Frenet sur le document réponse à rendre avec la copie.

Réponse :

6. Citer l’expression des coordonnées du vecteur accélération $\overrightarrow{a}_G$ dans le repère de Frenet, dans le cas d’un mouvement circulaire.

Réponse :

Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme :

$\vec{a}=\frac{v^2}{d_{LS}}\vec{N}+\frac{dv}{dt}\vec{T}$

7. En déduire l’expression de l’accélération $\overrightarrow{a}_G$ dans le repère de Frenet en fonction de G, M_L, d_LS et $\overrightarrow{N}$ .

Réponse :

$\overrightarrow{a}=-G\times \frac{M_{L}}{d_{LS}^2}\overrightarrow{u}$ (question 4)

$\overrightarrow{u}=-\overrightarrow{N}$

$\overrightarrow{a}=G\times \frac{M_{L}}{d_{LS}^2}\overrightarrow{N}$

8. Justifier que la vitesse V du satellite est constante et montrer que son expression dans le repère de Frenet en fonction de G, M_L, d_LS est :

$v= \sqrt{\frac{G \times M_L}{d_{LS}}}$

Réponse :

$\overrightarrow{a}=G\times \frac{M_{L}}{d_{LS}^2}\overrightarrow{N}$ (question 7)

$\vec{a}=\frac{v^2}{d_{LS}}\vec{N}+\frac{dv}{dt}\vec{T}$ (question 6)

L’accélération étant unique, par identification :

$\frac{v^2}{d_{LS}}=G\ \times \frac{M_L}{d_{LS}^2}$

donc

$v=\sqrt{\frac{G\times M_{L}}{d_{LS}}}$

Dans la question suivante, la qualité de la rédaction, la structuration de l’argumentation et la rigueur des calculs seront valorisées.

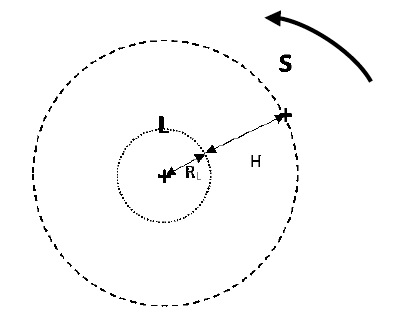
9. Démontrer que pour que le satellite soit fixe par rapport à la Lune, il doit être à une altitude H = 8,67 ×10⁷ m par rapport à la surface de la Lune.

B- Alunissage

Le vaisseau lunaire HLS (Human Landing System) a pour rôle de déposer deux astronautes sur le sol lunaire. À la surface, il sert d’habitat durant la mission d’une durée initiale d’environ une semaine puis il ramène l’équipage à la station spatiale.

Source : Wikipédia

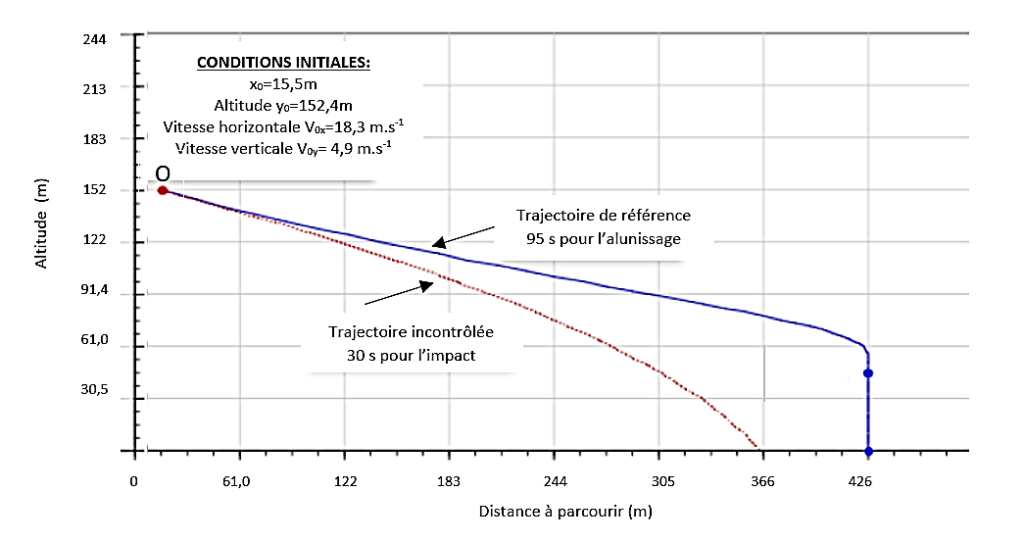
Une simulation de l’alunissage a été menée sur un simulateur de mouvement vertical (VMS). Cette simulation commence à 152,4 m d’altitude avec une vitesse horizontale de norme égale à 18,3 m.s^-1 et une vitesse verticale de norme égale à 4,9 m.s^-1(voir les conditions initiales de la figure 1).

La trajectoire de référence d’une durée de 95 s, permet de poser le module sur le sol lunaire en toute sécurité.

Une trajectoire incontrôlée d’une durée de 30 s qui conduirait à un impact sur le sol lunaire mettant un terme à la mission est représentée figure 1.

Source : AIAA Space 2008 Conference ,9 – 11 September 2008, San Diego, CA

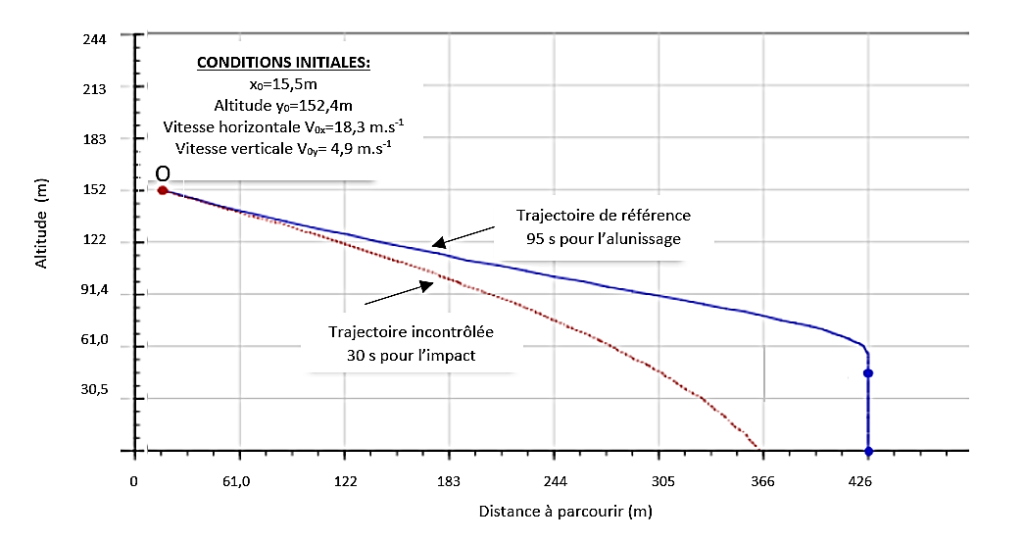
Figure 1. Trajectoires de référence et incontrôlée d’un atterrisseur lunaire dans le plan vertical
*Source : D’après AIAA Space 2008 Conference ,9 – 11 September 2008, San Diego, CA*

Données :

Valeur du champ de pesanteur sur la lune : g_L = 1,6 m.s^-2
Équations horaires d’une chute libre dans un champ de pesanteur uniforme avec un vitesse initiale $( \overrightarrow{V_0}$ non nulle :

$x(t)= v_{0x} \times t +x_0$ et $y(t)= - \frac{1}{2}\times g_L \times t^2+v_{0y} \times t +y_0$

𝑉_0x : norme de la vitesse horizontale et 𝑉_0x : norme de la vitesse verticale

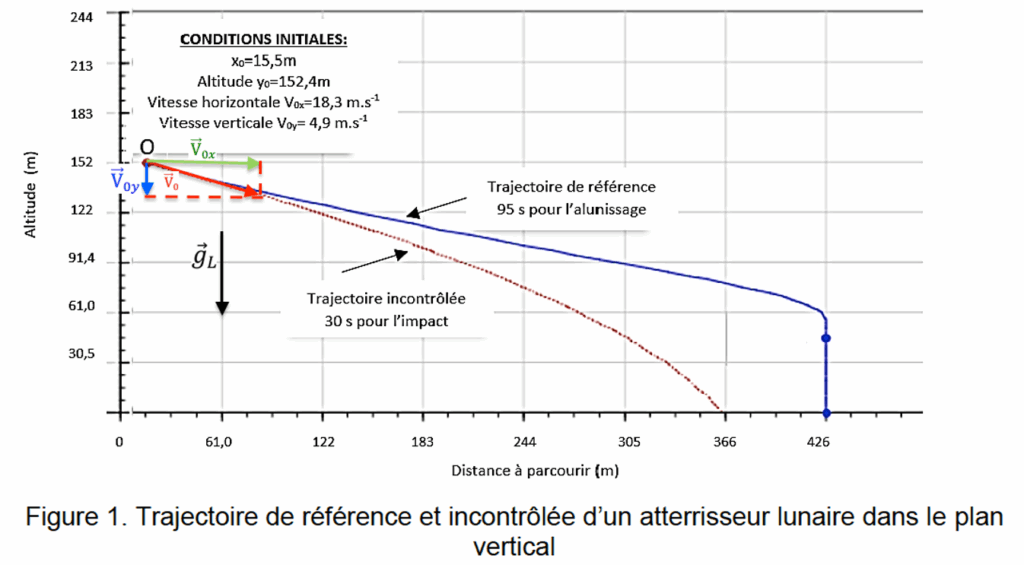
10. Sur le document réponse à rendre avec la copie, représenter au point O, de coordonnées x0 et y0, les vecteurs vitesse horizontale $\overrightarrow{V}_{0x}$ et vitesse verticale $\overrightarrow{V}_{0y}$ sans souci d’échelle. Représenter également le vecteur champ de pesanteur $\overrightarrow{g}_{L}$ .

11. Justifier le signe négatif ou positif de chacun des trois termes de l’expression :

$y(t)= - \frac{1}{2}\times g_L \times t^2-v_{0y} \times t +y_0$

12. À l’aide de l’équation horaire (1) et de la figure 1 calculer la durée t de descente de l’alunisseur s’il était en chute libre. Indiquer si l’alunisseur dans sa trajectoire incontrôlée est ou pas en chute libre.

EXERCICE B – L’installation de l’Homme sur la Lune DOCUMENT REPONSE A RENDRE AVEC LA COPIE

Partie A : Questions 2 et 5

Partie B : Question 10.