Mesure de la circonférence de la Terre

Sujet sans enseignement de mathématiques spécifique

Enseignement scientifique première

Durée 1h – 10 points – Thème « La Terre, un astre singulier »

Ératosthène de Cyrène est un astronome, géographe, philosophe et mathématicien grec du IIIe siècle av. J.-C. (né à Cyrène vers 276 av. J.-C. et mort à Alexandrie, en Égypte, vers 194 av. J.-C.). Il est connu pour avoir établi une méthode qui permet d’estimer la mesure de la circonférence de la Terre.

Il avait observé, qu’à midi, lors du solstice d’été, un puits situé à Syène (actuelle Assouan en Égypte) ne projetait aucune ombre, tandis qu’à Alexandrie, plus au nord, au même moment, un obélisque projetait une ombre mesurable.

Les deux villes, situées très proches d’un même méridien, sont à une distance l’une de l’autre estimée à 5 000 stades. (Un stade est une ancienne unité de longueur correspondant à la longueur du stade d’Olympie, soit environ 157,5 mètres).

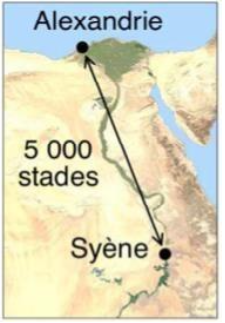
Document 1 – Modélisation de la démarche expérimentale d’Ératosthène

Le scaphé était un ancien instrument de mesure d’angle, de forme circulaire.

Partie 1 – Mesure de la circonférence de la Terre par la méthode d’Ératosthènec

À l’aide d’un scaphé, Ératosthène a mesuré que l’angle a correspondait à un cinquantième de tour du scaphé.

1 – Montrer que l’angle a mesure environ 7,2°.

1 tour	360°
un cinquantième de tour=1/50	a

$a=\frac{\frac{1}{50} \times 360}{1}$

a=7,2°

2 – Convertir la distance entre Alexandrie et Syène en kilomètres.

La distance entre Alexandrie et Syène est estimée à 5000 stades

157,5 mètres	1 stade
D	5000 stades

$D=\frac{5000 \times 157,5}{1}$

$D=787\ 500\ m$

D=787,5 km

3 – Justifier que les angles a et b du document 1 ont la même mesure.

Les rayons du soleil sont parallèles entre eux.

La droite partant du centre de la Terre vers Alexandrie coupe ces deux droites parallèles.

Les angles a et b sont alternes internent et sont donc de même valeur. b=a=7,2°

4 – En déduire la circonférence de la Terre en kilomètres.

La distance entre Alexandrie et Syène est de 787,5 km

Calculons la circonférence de la Terre :

787,5 km	7,2°
circonférence en stade	360°

circonférence en stade=787,5×360/7,2

circonférence en stade=39 375 km

Grâce à des mesures par satellite, on estime aujourd’hui la circonférence de la Terre à 40 075 km.

5 – Proposer une source d’erreur possible pour la valeur estimée par Ératosthène.

Source d’erreur possibles pour la valeur estimée par Eratosthène : La distance entre Alexandrie et Syène est estimée à 5000 stades (c’est une estimation qui n’est pas très précise).

Partie 2 – Construction d’un savoir scientifique

Quelques siècles avant Ératosthène, Anaxagore de Clazomènes (né à Clazomènes, en Turquie, vers 500 av. J.-C. et mort à Lampsaque, en Turquie également, en 428 av. J.-C.) avait effectué les mêmes mesures pour en déduire la distance entre la Terre et le Soleil, qu’il avait alors estimée à environ 6 500 km.

Document 2 – Présentation des méthodes d’Anaxagore et d’Ératosthène au solstice d’été à midi

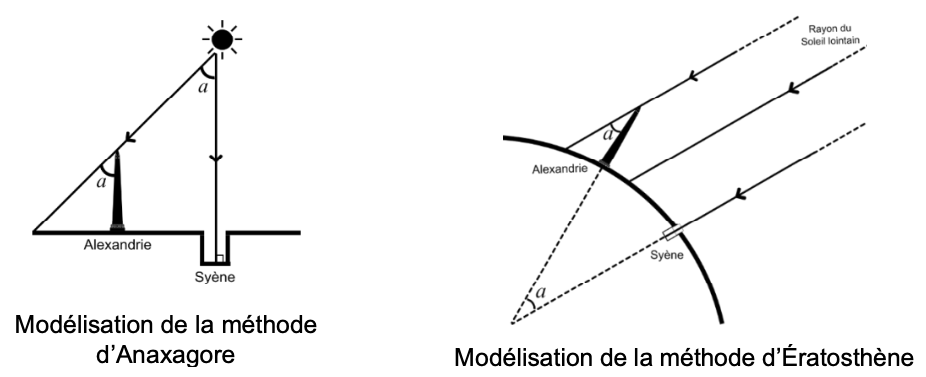
6 – Comparer les deux modélisations (observations, hypothèses, mesures réalisées, mesure obtenue) présentées dans le document 2.

Ératosthène et Anaxagore ont réalisé des observations astronomiques.

Ératosthène a observé que, lors du solstice d’été, un puits à Syène (Assouan) ne projetait aucune ombre, tandis qu’à Alexandrie, un obélisque projetait une ombre. Il a supposé la Terre sphérique et mesuré l’angle de l’ombre à Alexandrie. Connaissant la distance entre les villes, il a estimé la circonférence de la Terre à environ 39 375 km.

Anaxagore de Clazomènes, avait estimé la distance entre la Terre et le Soleil à environ 6 500 km. Il avait effectué des observations similaires, mais avec l’hypothèse que la Terre était plate et que les rayons provenant du Soleil n’étaient pas parallèles. Ces hypothèses ont conduit à une erreur immense sur la distance Terre-Soleil.

Ératosthène s’appuyait sur des mesures précises d’angles et de distances terrestres avec une hypothèse correcte de la sphéricité de la Terre, tandis qu’Anaxagore, en considérant la Terre plate et le Soleil proche, a obtenu une mesure fausse.

La pratique de la démarche scientifique concourt à la mise en cohérence de faits, à l’identification de paramètres pertinents, à l’élaboration de concepts et à la construction de modèles et de théories.

7 – Expliquer en quoi la méthode d’Ératosthène, pour établir la mesure de la circonférence de la Terre, est un exemple de démarche scientifique.

La méthode d’Ératosthène pour mesurer la circonférence de la Terre est un exemple de démarche scientifique car elle suit plusieurs étapes clés de la méthode scientifique, contribuant à la mise en cohérence de faits, à l’identification de paramètres pertinents, à l’élaboration de concepts et à la construction de modèles et de théories.

Ératosthène a commencé par observer des phénomènes naturels. Il a noté qu’à Syène, lors du solstice d’été, un puits ne projetait aucune ombre à midi, tandis qu’à Alexandrie, un obélisque projetait une ombre mesurable.

Il a formulé l’hypothèse que la Terre est sphérique. Cette hypothèse était essentielle pour interpréter correctement ses observations, notamment les différences dans les ombres projetées.

Il a mesuré l’angle de l’ombre à Alexandrie, trouvant un angle d’environ 7,2 degrés (1/50 de cercle complet). Il a également utilisé la distance entre Syène et Alexandrie, estimée à 5 000 stades (environ 787,5 km).

Ératosthène a modélisé la Terre comme une sphère. Il a utilisé les mesures collectées pour calculer la circonférence de la Terre.

Bien que les outils de l’époque ne permettaient pas de vérifier directement sa mesure, la précision de son estimation a été confirmée par des méthodes ultérieures, validant ainsi son modèle et ses hypothèses.

Cette démarche montre comment Ératosthène a utilisé l’observation, l’hypothèse, la collecte de données, la modélisation et le calcul pour parvenir à une conclusion scientifique précise.