Centres étrangers 2022 Sujet 2
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ2G11
Sujet et corrigé
Mots-clés: Lois de Newton, gravitation, mouvement des planètes et des satellites
En 1610, Galilée a été le premier à observer les quatre principaux satellites de Jupiter (Io, Europe, Ganymède et Callisto) en utilisant une lunette astronomique qu’il avait lui-même fabriquée.

Les lunettes de Galilée
(musée de Florence)
À la suite de Galilée, les observations de ces quatre satellites ont permis de réaliser les mesures regroupées dans le tableau ci-dessous.
| Satellite | Période de révolution T en jours (j) | Demi-grand axe a de la trajectoire elliptique (×105 km) |
| Io | 1,75 | 4,22 |
| Europe | 3,55 | 6,71 |
| Ganymède | 7,16 | 10,7 |
| Callisto | 16,7 | 18,8 |
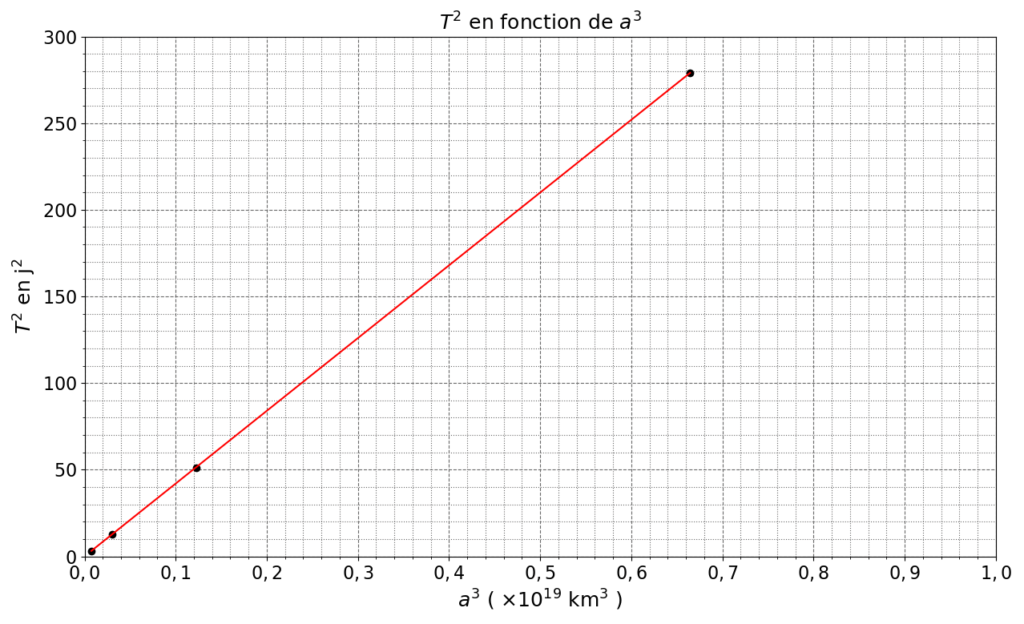
À l’aide d’un tableur, on a positionné les mesures dans un graphique donnant les variations de T 2 en fonction de celles de a3 pour les quatre satellites de Jupiter. Le tableur permet de superposer à ces points de mesure une modélisation par une droite (Cf. figure 1 ci-dessous).
Donnée : Constante de gravitation universelle 𝐺 = 6,67×10−11 m3⋅kg-1⋅s-2
Exploitation des résultats expérimentaux
1. À partir des résultats expérimentaux (figure 1), préciser la relation qui existe entre T 2 et a3 pour les quatre satellites de Jupiter. Donner le nom de la loi correspondante (établie en 1618).
Nous avons une droite qui passe par l’origine.
L’équation est de la forme :
$$T^2 = K a^3$$
D’où :
$$\frac{T^2}{a^3} = K$$
On retrouve la 3ᵉ loi de Kepler.
Modélisation du mouvement d’un satellite de Jupiter
On se place dans le cadre théorique de la mécanique de Newton (publiée en 1687) pour retrouver la relation évoquée dans la question 1 et déterminer la masse 𝑀𝐽 de Jupiter.
On étudie le mouvement du satellite dans le référentiel joviocentrique (centré sur Jupiter), supposé galiléen. On fait l’approximation que le mouvement du centre S du satellite est circulaire, centré sur le centre J de Jupiter, et on considère que la seule force qui s’applique sur le satellite est la force de gravitation $\overrightarrow{F_J_/_S} $ exercée par Jupiter sur le satellite.
On désigne par r la distance entre les centres des deux astres, par 𝑀𝐽 la masse de Jupiter et par m la masse du satellite.
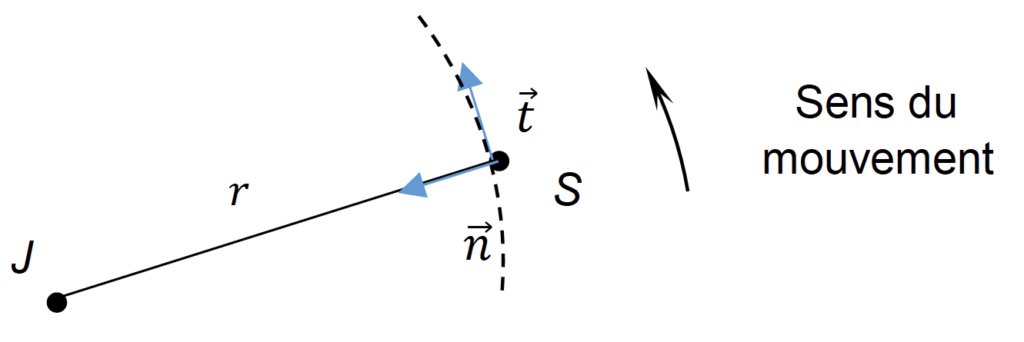
2. Sur un schéma, reprendre les éléments donnés sur la figure 2 et représenter sans souci d’échelle :
– Le vecteur vitesse $\overrightarrow{v_S} $ du satellite ;
-La force de gravitation $\overrightarrow{F_J_/_S} $ exercée par Jupiter sur le satellite.
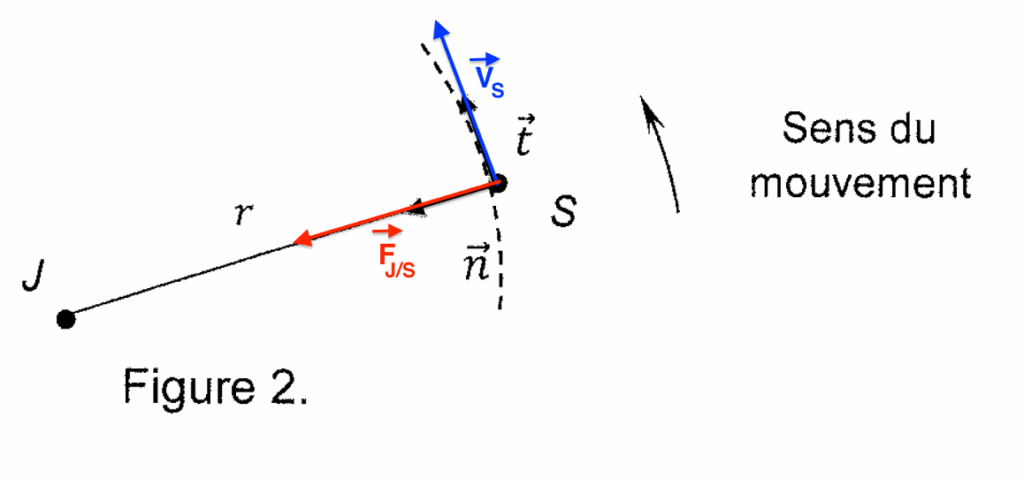
3. Donner l’expression de la force de gravitation $\overrightarrow{F_J_/_S} $ exercée par Jupiter sur le satellite en fonction de 𝑀𝐽, 𝑚, 𝐺, 𝑟 et $\overrightarrow{n} $.
Réponse :
$\overrightarrow{F}_{J/S}=G\times \frac{m\times M_{J}}{r^2}\overrightarrow{n}$
4. Appliquer la deuxième loi de Newton et en déduire l’expression de la vitesse 𝑉𝑆 du satellite en fonction de 𝐺, 𝑀𝐽 et 𝑟.
Réponse :
Système : satellite
Référentiel : joviocentrique supposé galiléen
D’après la 2nd loi de Newton :
$\sum_{}^{}\overrightarrow{F_{ext}}=m\overrightarrow{a}_{S}$
$\overrightarrow{F}_{J/S}=m\overrightarrow{a}_{S}$
$G\times \frac{m\times M_{J}}{r^2}\overrightarrow{n}=m\overrightarrow{a}_{S}$
$\overrightarrow{a}_{S}=G\times \frac{M_{J}}{r^2}\overrightarrow{n}$
Or, pour un mouvement circulaire, dans la base de Frenet, le vecteur accélération est de la forme :
$\vec{a}_{S}=\frac{v_{S}^2}{r}\vec{n}+\frac{dv_{S}}{dt}\vec{t}$
L’accélération étant unique, par identification :
$\frac{v_{S}^2}{r}=G\ \times \frac{M_J}{r^2}$
donc
$v_{S}=\sqrt{\frac{G\times M_{J}}{r}}$
5. En déduire que, dans le cadre de l’approximation du mouvement circulaire, le quotient T2/R3 est égal à $ \frac{4 \pi^2}{GM_J} $
Réponse :
La période de révolution est :
$T=\frac{circonference}{vitesse}$
$T=\frac{2\pi r}{v_{S}}$
$T=\frac{2\pi r}{\sqrt{\frac{G\times M_{J}}{r}}}$
$T=2\pi r \sqrt{\frac{r}{G\times M_{J}}}$
$T^2=4\pi^2 r^2 \frac{r}{G\times M_{J}}$
$T^2= \frac{4\pi^2r^3}{G\times M_{J}}$
$\frac{T^2}{r^3}= \frac{4\pi^2}{G\times M_{J}}$
6. À l’aide des résultats expérimentaux, calculer la valeur de la masse 𝑀𝐽 de Jupiter. Commenter un éventuel écart à la valeur tabulée : 1,898 6 x 1027 kg.
Aide éventuelle : 1 j2 ∙ km−3 = 7,46 s2 ∙ m−3
$$\frac{T^2}{r^3} = \frac{4\pi^2}{G \times M_J}$$
Or $\frac{T^2}{r^3} = K$ (Question 1.)
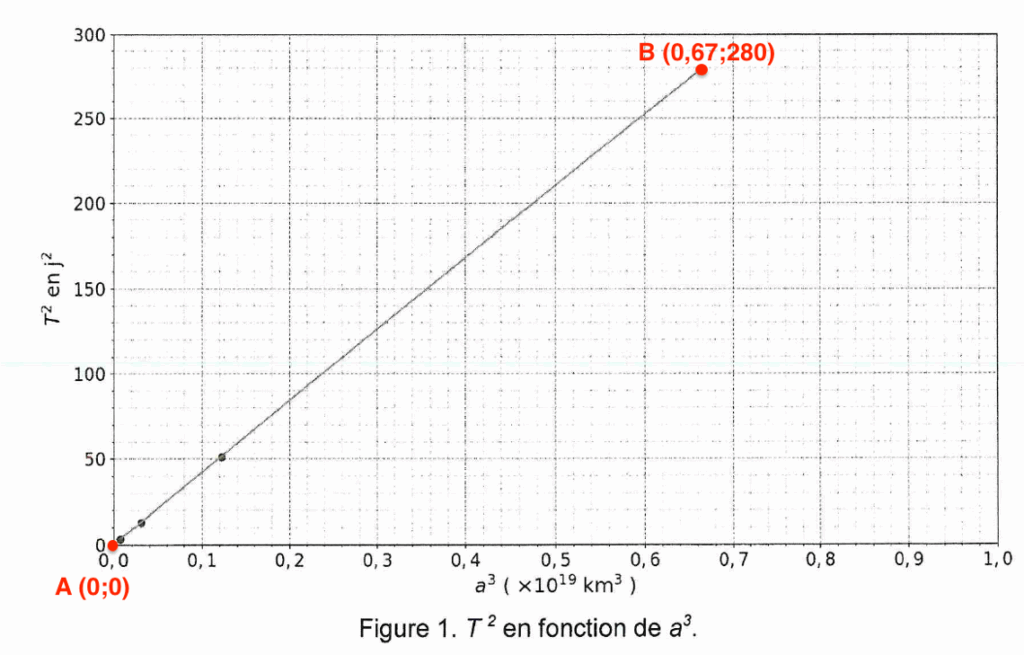
Calculons $K$, le coefficient directeur :
$$K = \frac{y_B – y_A}{x_B – x_A}$$
$$K = \frac{280 – 0}{0,67 \times 10^{19} – 0}$$
$$K = 4,2 \times 10^{-17}\ j^2 \cdot km^{-3}$$
$$K = 4,2 \times 10^{-17} \times 7,46$$
$$K = 3,1 \times 10^{-16}\ s^2 \cdot m^{-3}$$
On a :
$$\frac{T^2}{r^3} = \frac{4\pi^2}{G \times M_J}$$
$$K = \frac{4\pi^2}{G \times M_J}$$
$$M_J = \frac{4\pi^2}{G \times K}$$
$$M_J = \frac{4\pi^2}{6,67 \times 10^{-11} \times 3,1 \times 10^{-16}}$$
$$M_J = 1,9 \times 10^{27}\ kg$$
Ce résultat est très proche de la valeur tabulée.
La relation établie à la question 5 pour le système composé de Jupiter et de ses satellites est universelle et est applicable à d’autres systèmes constitués de satellites en orbite autour d’un astre central.
7. Déterminer la masse du Soleil.
Donnée : la distance entre la Terre et le Soleil est de 150 millions de kilomètres.
Le candidat est invité à faire preuve d’initiative, à justifier ses choix et à présenter sa démarche. Certaines valeurs numériques nécessaires aux calculs sont supposées connues du candidat.
La relation établie est applicable au système Terre–Soleil.
Ainsi :
$$\frac{T_T^2}{d_{TS}^3} = \frac{4\pi^2}{G \times M_S}$$
$$T_T^2 \times G \times M_S = 4\pi^2 \times d_{TS}^3$$
$$M_S = \frac{4\pi^2 \times d_{TS}^3}{T_T^2 \times G}$$
$$M_S = \frac{4\pi^2 \times (150 \times 10^6 \times 10^3)^3}{(365,25 \times 24 \times 60 \times 60)^2 \times 6,67 \times 10^{-11}}$$
$$M_S = 2,0 \times 10^{30}\ kg$$
