Métropole 2025 Sujet 2
Exercice 1 – (11 points) – Durée 1h56 – Calculatrice autorisée
Sujet n°25-PYCJ2ME1
Sujet et corrigé
Exercice 1 – Mesure de l’épaisseur d’un film alimentaire (11 points)
Les films alimentaires étirables sont des films plastiques souples et transparents utilisés principalement pour conserver les aliments. Ils sont fabriqués en polymères tels que le polyéthylène basse densité (PEBD) et parfois le polychlorure de vinyle (PVC). Ces films offrent une barrière contre l’air, l’humidité et les contaminants, aidant ainsi à prolonger la fraîcheur des aliments et à réduire les déchets alimentaires. L’épaisseur du film est un paramètre essentiel des propriétés mécaniques (élasticité, résistance à la traction) des films étirables, ainsi que de leur impact écologique.

L’objectif de cet exercice est d’étudier différentes méthodes de détermination de l’épaisseur d’un film alimentaire.
1. Mesure de l’épaisseur d’un film alimentaire par capacimétrie
Données :
- un condensateur plan est constitué de deux armatures métalliques, parallèles entre elles, chacune de surface S, séparées par un matériau isolant (papier, plastique) d’épaisseur e ;
- expression littérale de la capacité C d’un tel condensateur :
$$C= \frac{\varepsilon_0\cdot \varepsilon_r \cdot S}{e}$$
avec :
• ε0 = 8,85×10–12 F·m–1 : permittivité du vide ;
• εr : permittivité relative du matériau isolant ;
On réalise un condensateur plan en intercalant entre deux feuilles de papier aluminium rectangulaires, de dimensions 21 cm × 28 cm, une seule couche du film transparent d’épaisseur e. On note C sa capacité. La figure 1 ci-dessous présente un schéma de ce dispositif.

Figure 1. Vue en coupe du condensateur plan
On réalise ensuite le montage, schématisé en figure 2, constitué du condensateur réalisé, d’un conducteur ohmique de résistance R = 1,00 kΩ, d’un interrupteur et d’un générateur idéal délivrant une tension continue E = 4,9 V.

Figure 2. Schéma du montage électrique
On étudie la charge du condensateur à partir de la date t = 0, date à laquelle l’interrupteur est fermé. L’évolution temporelle de la tension uC aux bornes du condensateur est présentée en figure 3.
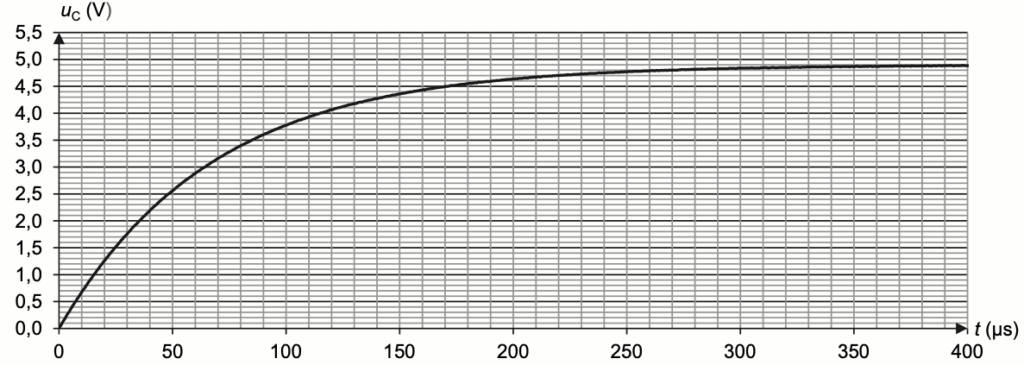
Figure 3. Évolution de la tension aux bornes du condensateur en fonction du temps
Q1. Établir l’équation différentielle ci-dessous vérifiée par la tension uC aux bornes du condensateur, où τ est le temps caractéristique dont on donnera l’expression :
$$\frac{du_C}{dt} + \frac{1}{\tau}u_C = \frac{E}{\tau}$$
D’après la loi d’additivité des tensions ou loi des mailles :
$$U_C(t)+U_R(t)=E$$
or $$U_R(t)=R\times i$$
$$U_C(t)+R\times i\ =E$$
Or
$$i(t)=\frac{dq_{(t)}}{dt}$$
$$U_C(t)+R\times \frac{dq_{(t)}}{dt}\ =E$$
Or
$$q(t)=C\times U_C(t)$$
$$U_C(t)+R\times \frac{dC\times U_C(t)}{dt}\ =E$$
$$U_C(t)+RC\frac{dU_C(t)}{dt}=E$$
On divise par RC :
$$\frac{U_C(t)}{RC}+\frac{dU_C(t)}{dt}=\frac{E}{RC}$$
$$\frac{dU_C(t)}{dt}+\frac{1}{RC}\times U_C(t)=\frac{E}{RC}$$
Avec $$\tau=RC$$ :
$$\frac{dU_C(t)}{dt}+\frac{1}{\tau}\times U_C(t)=\frac{E}{\tau}$$
La solution de cette équation différentielle est : $u_C(t)=A\cdot (1-e^{-t/\tau})$ où A est une constante.
Q2. Déterminer l’expression de la constante A.
Méthode 1 :
$$U_C\left(t\rightarrow\infty \right)=A\left(1-e^{-\frac{\infty }{\tau}}\right)$$
$$U_C\left(t\rightarrow\infty \right)=A\left(1-0\right)$$
$$U_C\left(t\rightarrow\infty \right)=A$$
Or pour un temps très long, la tension du condensateur prend pour valeur la tension du générateur : $$U_C\left(t\rightarrow\infty \right)=E$$
Ainsi $$A=E$$
Méthode 2 :
Vérifions que la solution de cette équation différentielle est de la forme :
$$U_C\left(t\right)=A\left(1-e^{-\frac{t}{\tau}}\right)$$
-Dérivons $$U_C\left(t\right)$$ :
$$\frac{dU_C(t)}{dt}=A\times -1\times \frac{-1}{\tau}e^{-\frac{t}{\tau}}$$
$$\frac{dU_C(t)}{dt}=\frac{A}{\tau}e^{-\frac{t}{\tau}}$$
-Remplaçons $$U_C\left(t\right)$$ et $$\frac{dU_C(t)}{dt}$$ dans l’équation :
$$\frac{dU_C(t)}{dt}+\frac{1}{\tau}\times U_C(t)=\frac{E}{\tau}$$
$$\frac{A}{\tau}e^{-\frac{t}{\tau}}+\frac{1}{\tau}\times A\left(1-e^{-\frac{t}{\tau}}\right)=\frac{E}{\tau}$$
$$\frac{A}{\tau}e^{-\frac{t}{\tau}}+\frac{A}{\tau}-\frac{Ae^{-\frac{t}{\tau}}}{\tau}=\frac{E}{\tau}$$
$$\frac{A}{\tau}=\frac{E}{\tau}$$
$$A=E$$
La solution de la forme $$U_C\left(t\right)=A\left(1-e^{-\frac{t}{\tau}}\right)$$ vérifie l’équation différentielle avec $$A=E$$. Ainsi : $$U_C\left(t\right)=E\left(1-e^{-\frac{t}{\tau}}\right)$$
Q3. Exprimer, en fonction de E, la tension uc(𝜏) aux bornes du condensateur à la date t = τ.
$$U_C\left(t=\tau\right)=E\left(1-e^{-\frac{\tau}{\tau}}\right)$$
$$U_C\left(t=\tau\right)=E\left(1-0,37\right)$$
$$U_C\left(t=\tau\right)=0,63\times E$$
Q4. Exploiter la courbe de la figure 3 et le résultat obtenu à la question Q3 pour déterminer la valeur de la constante de temps τ du circuit. Expliciter la démarche utilisée.
$\tau$ peut être déterminée graphiquement :
$$U_C\left(\tau\right)=0,63\times E$$
$$U_C\left(\tau\right)=0,63\times 4,9$$
$$U_C\left(\tau\right)=3,1\ V$$
Graphiquement, pour $$U_C\left(\tau\right)=3,1\ V$$, on lit $$\tau=68\ \mu s$$
Q5. En déduire une valeur expérimentale de la capacité C du condensateur.
$$\tau=RC$$
$$C=\frac{\tau}{R}$$
$$C=\frac{68\times {10}^{-6}}{1,0\times {10}^3}$$
$$C=6,8\times {10}^{-8}\ F$$
Des mesures complémentaires répétées ont permis de déterminer une valeur moyenne de la capacité du condensateur : C = 69,8 nF.
Q6. Déterminer la valeur de l’épaisseur efilm du film alimentaire déduite de cette valeur moyenne. Avec cette méthode, l’incertitude-type sur l’épaisseur du film a pour valeur : u(efilm) = 1,0 µm.
$$C=\frac{\varepsilon_0\times \varepsilon_r\times S}{e}$$
$$C\times e=\varepsilon_0\times \varepsilon_r\times S$$
$$e_{film}=\frac{\varepsilon_0\times \varepsilon_{r,film}\times S}{C}$$
Or
$$S=l\times L$$
$$e_{film}=\frac{\varepsilon_0\times \varepsilon_{r,film}\times l\times L}{C}$$
$$e_{film}=\frac{8,85\times {10}^{-12}\times 2,3\times 21\times {10}^{-2}\times 28\times {10}^{-2}}{69,8\times {10}^{-9}}$$
$$e_{film}=1,7\times {10}^{-5}\ m$$
$$e_{film}=17\ \mu m$$
Q7. Discuter de l’accord du résultat obtenu à la question Q6 avec la valeur de l’épaisseur de référence du film indiquée dans les données.
D’après les données : pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient :
$$\frac{\left|x-x_{ref}\right|}{u\left(x\right)}$$
$$\frac{\left|e_{film}-e_{film,ref}\right|}{u\left(e_{film}\right)}=\frac{\left|17-7,6\right|}{1,0}$$
$$\frac{\left|e_{film}-e_{film,ref}\right|}{u\left(e_{film}\right)}=9,4$$
$$\frac{\left|e_{film}-e_{film,ref}\right|}{u\left(e_{film}\right)}>2$$
Ainsi, la valeur obtenue à la question Q6 n’est pas compatible avec la valeur de référence.
Pour expliquer l’écart observé, on peut faire l’hypothèse qu’il existe entre les feuilles d’aluminium, en plus de l’épaisseur du film alimentaire, une fine couche d’air d’épaisseur eair constante. La situation est alors schématisée sur la figure 4 ci-dessous.
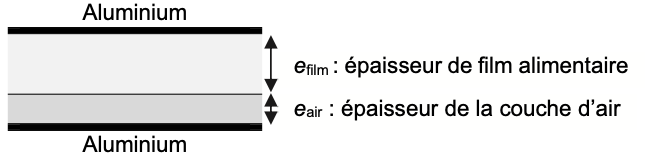
Figure 4. Couche d’air piégée dans le condensateur
On montre que la capacité C‘ d’un condensateur, dans le cas où le condensateur comprend une épaisseur d’air eair et une épaisseur de film efilm, est donnée par la relation :
$$C’ = \frac{\varepsilon_0 S}{\frac{e_{\text{air}}}{\varepsilon_{r,\text{air}}} + \frac{e_{\text{film}}}{\varepsilon_{r,\text{film}}}}$$
Q8. En envisageant deux cas limites au schéma présenté en figure 4, vérifier que l’expression donnée ci- dessus est compatible avec l’expression littérale de la capacité d’un condensateur précisée dans les données.
$$C\prime=\frac{\varepsilon_0\times S}{\frac{e_{air}}{\varepsilon_{r,air}}+\frac{e_{film}}{\varepsilon_{r,film}}}$$
Cas limites :
Il n’y a pas d’air : $$e_{air}=0$$
$$C\prime=\frac{\varepsilon_0\times S}{\frac{e_{air}}{\varepsilon_{r,air}}+\frac{e_{film}}{\varepsilon_{r,film}}}$$
$$C\prime=\frac{\varepsilon_0\times S}{\frac{0}{\varepsilon_{r,air}}+\frac{e_{film}}{\varepsilon_{r,film}}}$$
$$C\prime=\frac{\varepsilon_0\times S}{\frac{e_{film}}{\varepsilon_{r,film}}}$$
$$C\prime=\varepsilon_0\times S\times \frac{\varepsilon_{r,film}}{e_{film}}$$
$$C\prime=\frac{\varepsilon_0\times \varepsilon_{r,film}\times S}{e_{film}}$$
L’expression est compatible avec l’expression littérale de la capacité d’un condensateur : $$C=\frac{\varepsilon_0\times \varepsilon_r\times S}{e}$$
Il n’y a pas de film : $$e_{film}=0$$
$$C\prime=\frac{\varepsilon_0\times S}{\frac{e_{air}}{\varepsilon_{r,air}}+\frac{e_{film}}{\varepsilon_{r,film}}}$$
$$C\prime=\frac{\varepsilon_0\times S}{\frac{e_{air}}{\varepsilon_{r,air}}+\frac{0}{\varepsilon_{r,film}}}$$
$$C\prime=\frac{\varepsilon_0\times S}{\frac{e_{air}}{\varepsilon_{r,air}}}$$
$$C\prime=\varepsilon_0\times S\times \frac{\varepsilon_{r,air}}{e_{air}}$$
$$C\prime=\frac{\varepsilon_0\times \varepsilon_{r,air}\times S}{e_{air}}$$
L’expression est compatible avec l’expression littérale de la capacité d’un condensateur : $$C=\frac{\varepsilon_0\times \varepsilon_r\times S}{e}$$
Q9. Dans ce modèle, déterminer la valeur d’épaisseur d’air eair en considérant que l’épaisseur du film alimentaire est celle de référence : efilm,ref = 7,6 µm. Commenter.
$$C\prime=\frac{\varepsilon_0\times S}{\frac{e_{air}}{\varepsilon_{r,air}}+\frac{e_{film}}{\varepsilon_{r,film}}}$$
$$C\prime\times \left(\frac{e_{air}}{\varepsilon_{r,air}}+\frac{e_{film}}{\varepsilon_{r,film}}\right)=\varepsilon_0\times S$$
$$\frac{e_{air}}{\varepsilon_{r,air}}+\frac{e_{film}}{\varepsilon_{r,film}}=\frac{\varepsilon_0\times S}{C\prime}$$
$$\frac{e_{air}}{\varepsilon_{r,air}}=\frac{\varepsilon_0\times S}{C\prime}-\frac{e_{film}}{\varepsilon_{r,film}}$$
$$e_{air}=\left(\frac{\varepsilon_0\times S}{C\prime}-\frac{e_{film}}{\varepsilon_{r,film}}\right)\times \varepsilon_{r,air}$$
$$e_{air}=\left(\frac{8,85\times {10}^{-12}\times 21\times {10}^{-2}\times 28\times {10}^{-2}}{69,8\times {10}^{-9}}-\frac{7,6\times {10}^{-6}}{2,3}\right)\times 1,0$$
$$e_{air}=4,2\times {10}^{-6}\ m$$
$$e_{air}=4,2\ \mu m$$
L’épaisseur d’air n’est pas négligeable.
2. Mesure de l’épaisseur du film alimentaire par pesée
Données :
- dimensions du film alimentaire indiquées sur l’emballage : largeur l = 29 cm et longueur L = 30 m ;
- masse volumique du polymère constituant le film alimentaire : ρfilm = 1,25×103 kg.m–3.
Afin d’estimer un ordre de grandeur de l’épaisseur du film alimentaire, on mesure la masse de film d’un rouleau neuf : mfilm = 70,56 g.
Q10. Calculer l’épaisseur efilm du film alimentaire dans le rouleau.
$$\rho_{film}=\frac{m_{film}}{V}$$
Or
$$V=e\times l\times L$$
D’où
$$\rho_{film}=\frac{m_{film}}{e\times l\times L}$$
$$e\times \rho_{film}=\frac{m_{film}}{l\times L}$$
$$e=\frac{m_{film}}{\rho_{film}\times l\times L}$$
$$e=\frac{70,56\times {10}^{-3}}{1,25\times {10}^3\times 29\times {10}^{-2}\times 30}$$
$$e=6,5\times {10}^{-6}m$$
$$e=6,5\ \ \mu m$$
3. Mesure de l’épaisseur du film alimentaire par interférométrie
Dans le but d’obtenir une mesure plus exacte de l’épaisseur du film alimentaire, on utilise une méthode interférométrique dans laquelle on éclaire le film avec une source lumineuse comme indiqué sur la figure 5 ci-dessous.
On ne s’intéresse dans cette étude qu’à deux rayons lumineux et issus d’un même rayon incident, comme représenté sur la figure 5 :
- rayon ➀ : rayon issu du rayon incident qui est réfléchi sur la surface supérieure du film alimentaire ;
- rayon ➁ : rayon issu du rayon incident qui est transmis dans le film puis réfléchi par la surface inférieure du film et qui ressort par la surface supérieure du film.
Les rayons ➀ et ➁ sont parallèles entre eux. Grâce à une lentille, ils se superposent à l’entrée d’une fibre optique, elle-même reliée à un spectromètre.
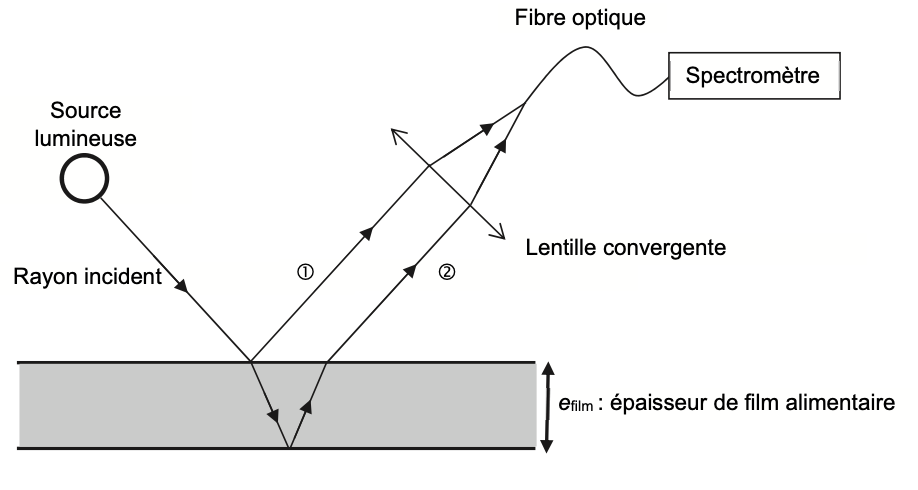
Figure 5. Dispositif expérimental
Pour une source monochromatique de longueur d’onde l, la superposition des deux ondes associées aux rayons ➀ et ➁ donne lieu à des interférences. On note δ la différence de chemin optique entre les deux ondes.
Q11. Préciser la relation entre δ et λ permettant d’obtenir des interférences constructives.
Pour observer des interférences constructives, il faut que : $$\delta=k\times \lambda$$.
L’ordre d’interférence p est, dans le cas général, défini comme le rapport p = δ. On admet que, dans les conditions de l’expérience, l’ordre d’interférence p est donné par la relation suivante :
$$p = \frac{\beta \times e_{\text{film}}}{\lambda} + \frac{1}{2} \qquad \text{relation 1}$$
où β est un paramètre sans dimension dépendant de l’indice de réfraction du film et de l’angle d’incidence de la lumière sur le film.
Q12. Préciser, en justifiant sans calcul, le phénomène observé lorsque le rapport $ \frac{\beta\times e_{\text{film}}}{\lambda}$ est un nombre entier.
$$p=\frac{\delta}{\lambda}$$
$$\frac{\delta}{\lambda}=p$$
$$\delta=p\times \lambda$$
Or
$$p=\frac{\beta\times e_{film}}{\lambda}+\frac{1}{2}$$
D’où
$$\delta=\left(\frac{\beta\times e_{film}}{\lambda}+\frac{1}{2}\right)\times \lambda$$
Pour $$\frac{\beta\times e_{film}}{\lambda}$$ un nombre entier
$$\frac{\beta\times e_{film}}{\lambda}=k$$
D’où
$$\delta=\left(k+\frac{1}{2}\right)\times \lambda$$
Lorsque le rapport $$\frac{\beta\times e_{film}}{\lambda}$$ est un nombre entier, les interférences observées seront destructives.
Dans l’expérience étudiée, le film est éclairé en lumière blanche et on analyse le spectre de la lumière transportée par la fibre. On donne ci-dessous sur la figure 6a le spectre de la lumière incidente et sur la figure 6b celui de la lumière captée par la fibre optique.
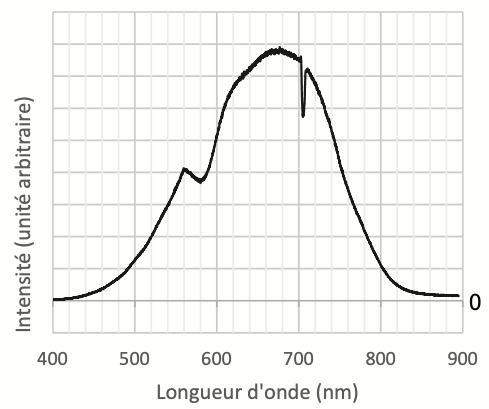
Figure 6a. Spectre de la lumière incidente

Figure 6b. Spectre de la lumière captée par la fibre optique
Q13. Le spectre de la figure 6b présente des maxima d’intensité dont certains sont entourés en pointillés. Expliquer leur origine.
Les maximas d’intensité sont des zones d’interférences constructives.
L’analyse de la figure 6b permet de représenter l’évolution de l’ordre d’interférence en fonction de l’inverse de la longueur d’onde. Les résultats obtenus et leur modélisation sont représentés sur la figure 7.

Figure 7. Représentation graphique de l’ordre d’interférence p en fonction de 1/𝜆
Q14. Indiquer, en justifiant, si les résultats expérimentaux sont cohérents avec la relation 1.
Relation 1 :
$$p=\frac{\beta\times e_{film}}{\lambda}+\frac{1}{2}$$
$$p=\beta\times e_{film}\times \frac{1}{\lambda}+\frac{1}{2}$$ Les résultats expérimentaux donnent la relation
$$p=22443\times \frac{1}{\lambda}+0,51$$
Les résultats expérimentaux sont compatibles avec la relation 1 avec : $$\beta\times e_{film}=22443\times {10}^{-9}$$
Remarque : on met $$\times {10}^{-9}$$ car λ est en nm.
Q15. Déduire de ces mesures la valeur de l’épaisseur efilm du film alimentaire, sachant que, dans les conditions de l’expérience, β = 3,02. Commenter.
$$\beta\times e_{film}=22443\times {10}^{-9}$$
$$e_{film}=\frac{22443\times {10}^{-9}\ }{\beta}$$
$$e_{film}=\frac{22443\times {10}^{-9}}{3,02}$$
$$e_{film}=7,4\times {10}^{-6}\ m$$
$$e_{film}=7,4\ \mu m$$
L’épaisseur trouvée correspond à l’épaisseur de référence $$7,6\ \mu m$$.
