Enseignement scientifique première
Durée 1h – 10 points – Thème « La Terre, un astre singulier »
[latexpage]
Eratosthène de Cyrène est un astronome, géographe, philosophe et mathématicien grec du IIIe siècle av. J.-C. (né à Cyrène, v. -276 et mort à Alexandrie, Egypte, v. -194). Eratosthène fut nommé́ à la tête de la bibliothèque d’Alexandrie vers -245 à la demande de Ptolémée III, pharaon d’Egypte, et fut précepteur de son fils Ptolémée IV.
Il est célèbre pour avoir établi la première méthode connue de mesure de la circonférence de la Terre.
Document 1 : données
• Le 21 juin, à midi, à Syène (Assouan), on voit le fond des puits.
• Le 21 juin, à midi, à Alexandrie, on mesure la longueur de l’ombre d’un gnomon* de 1 mètre. Celle-ci vaut 0,126 mètre.
• La distance entre Alexandrie et Syène est estimée à 5000 stades.
• Un stade est une unité de longueur correspondant à la longueur du stade d’Olympie, soit environ 157,5 mètres.
• Alexandrie et Syène sont supposées être sur un même méridien.
Le soleil étant lointain, on suppose que les rayons qu’il émet sont parallèles.
(*un gnomon est un instrument astronomique qui visualise par son ombre les déplacements du Soleil. Sa forme la plus simple est un bâton planté verticalement dans le sol.)
Document 2 : Calcul de la circonférence de la Terre par la méthode dite d’Ératosthène
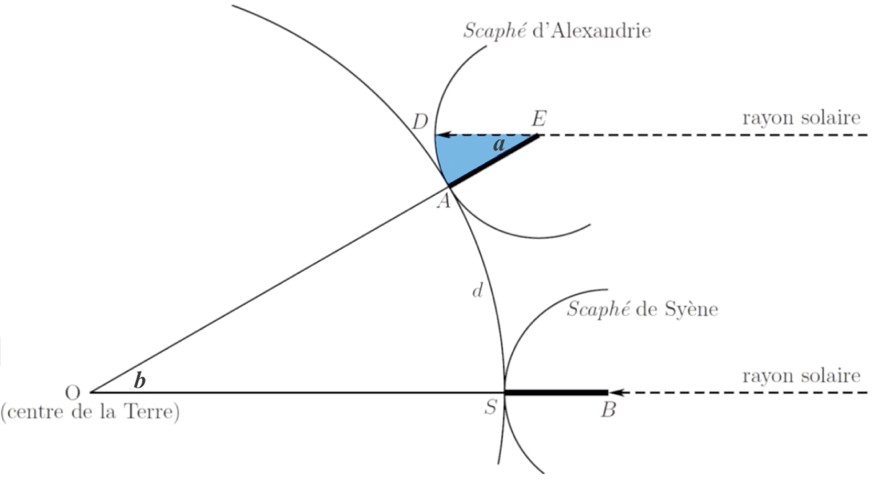
1 – Proposer un schéma représentant le gnomon, son ombre et les rayons du soleil avec les longueurs données dans le document 1 (il n’est pas demandé que le schéma soit à l’échelle).
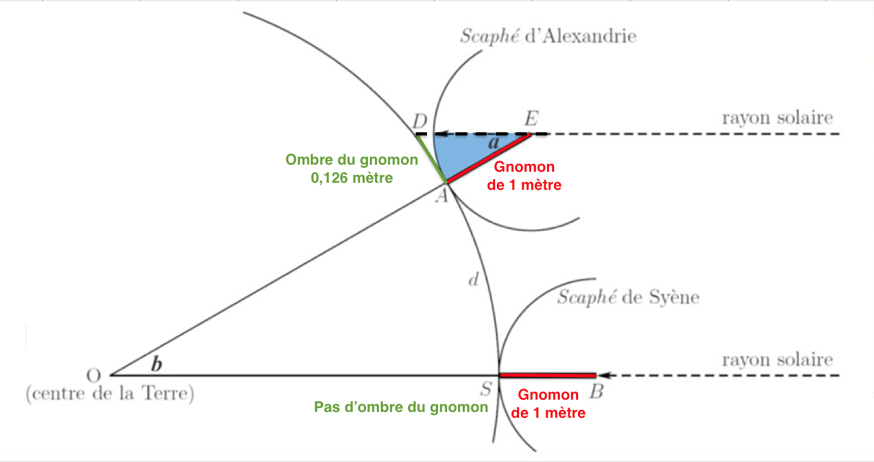
2 – Calculer la tangente de l’angle a formé par le gnomon et le rayon de soleil, et démontrer que cet angle mesure environ 7,2 °. On rappelle que, dans un triangle rectangle, la tangente d’un angle est égale au rapport du côté opposé sur le côté adjacent.
\[tan(a)=\frac{\textrm{côté opposé}}{\textrm{côté adjacent}} \]
\[tan(a)=\frac{\textrm{Ombre du gnomon}}{\textrm{Longueur du gnomon}} \]
\[tan(a)=\frac{0,126}{1} \]
tan(a)=0,126
a=arctan(0,126)=7,18°
L’angle a formé par le gnomon et le rayon de soleil mesure environ 7,2°.
3 – À l’aide d’un scaphé (instrument de mesure ancien, sorte de cadran solaire), Ératosthène a trouvé que l’angle a correspondait à un cinquantième de tour. Comparer avec le résultat de la question précédente.
| 1 tour | 360° |
| un cinquantième de tour=1/50 | a |
a=(1/50×360)/1
a=7,2°
Le résultat trouvé est identique de la question précédente.
4 – Préciser la distance qui mesure 5000 stades sur la représentation de la Terre du document 2.
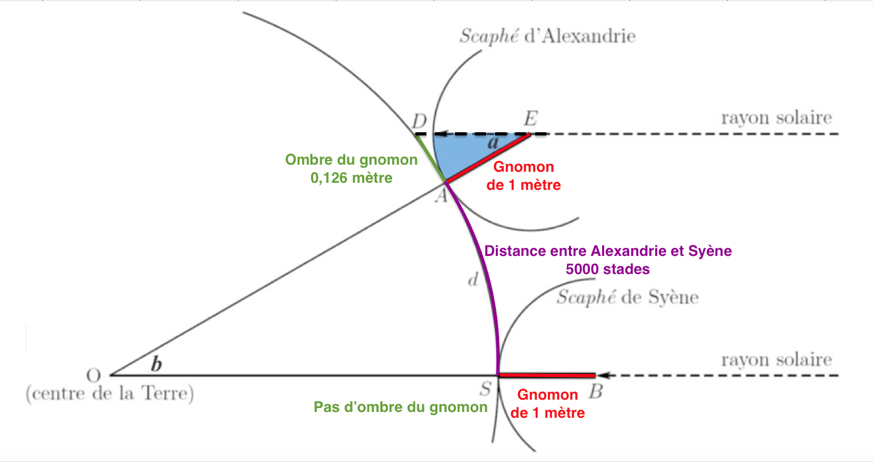
La distance AS entre Alexandrie et Syène est estimée à 5000 stades.
5 – Justifier que les angles a et b du document 2 ont la même mesure.
En déduire la circonférence de la Terre d’abord en stade, puis en kilomètre.
Les rayons du soleil sont parallèles entre eux. La droite partant du centre de la Terre vers Alexandrie coupe ces deux droites parallèles. Les angles a ̂ et b ̂ sont alternes internent et sont donc de même valeur. b ̂=a ̂=7,2°
La distance entre Alexandrie et Syène est estimée à 5000 stades.
Calculons la circonférence de la Terre en stade:
| 5 000 stades | 7,2° |
| circonférence en stade | 360° |
circonférence en stade=(5 000×360)/7,2
circonférence en stade=250 000 stades
D’après l’énonce : Un stade est une unité de longueur correspondant à la longueur du stade d’Olympie, soit environ 157,5 mètres.
Calculons la circonférence de la Terre en kilomètre :
| 1 stade | 157,5 m=0,1575 km |
| 250 000 stades | circonférence en kilomètre |
circonférence en kilomètre=(250 000 ×0,1575)/1
circonférence en kilomètre=39 375 km
6 – Grâce à des mesures par satellites, on estime aujourd’hui la circonférence de la Terre à 40 075 km. Proposer au moins une source d’erreur possible pour la valeur estimée par Eratosthène.
Sources d’erreurs possibles pour la valeur estimée par Eratosthène:
- Alexandrie et Syène sont supposées être sur un même méridien (il sont légèrement décalés).
- La distance entre Alexandrie et Syène est estimée à 5000 stades (c’est une estimation qui n’est pas très précise).
