Modélisation d’un service au tennis

Nouvelle Calédonie 2022 Sujet 2

Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 22-PYCJ2NC1

Mots clés de l’EXERCICE B : mouvement dans un champ de pesanteur uniforme, lois de Newton, étude énergétique.

L’objectif de cet exercice est de modéliser la trajectoire d’une balle de tennis lors d’un service et de confronter ce modèle à la réalité d’un service analysé par pointage vidéo de la balle.

Les règles du jeu standard indiquent que le serveur doit se tenir alternativement derrière la moitié droite et la moitié gauche du court. La balle doit passer en diagonale au-dessus du filet et toucher le sol dans le carré de service opposé avant que le relanceur ne la renvoie.

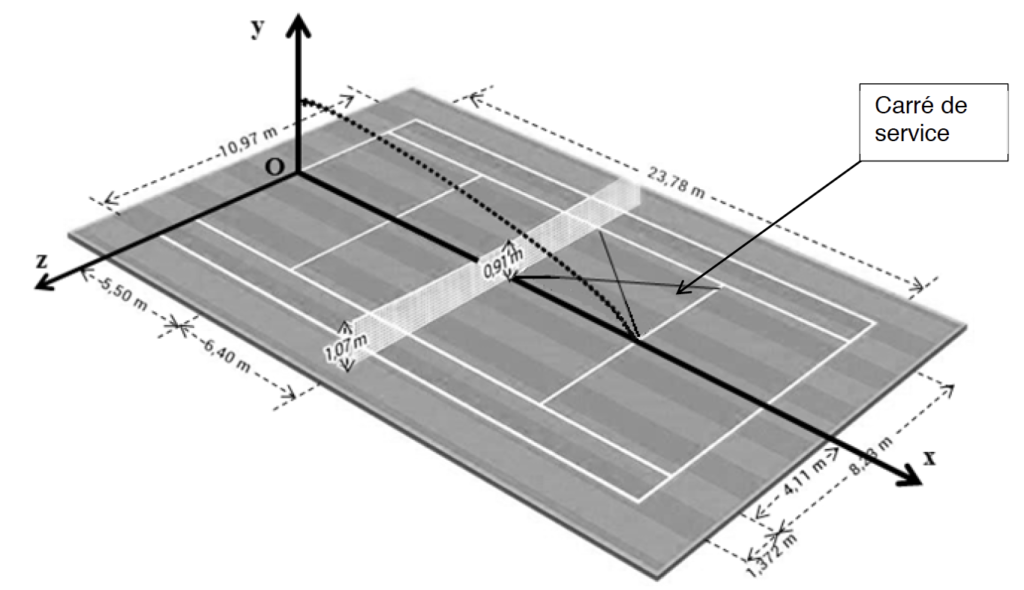
**Figure 1 : Dimensions d’un terrain de tennis (Source : club de Westhouse)**

Schéma sans échelle des trajectoires de deux services « à plat »

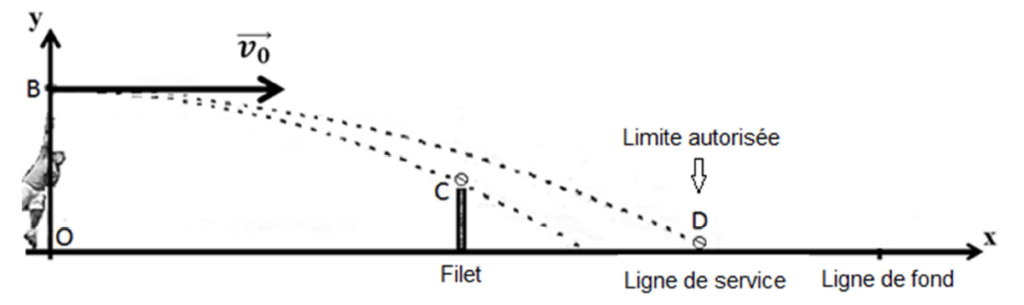
Les bases du modèle choisi

La masse de la balle dont le mouvement est modélisé est m = 58 g. Le service est effectué à plat. La balle sera modélisée par un point correspondant à son centre de masse G. L’étude est réalisée dans le référentiel terrestre supposé galiléen. Plusieurs hypothèses seront faites dans le cadre de cette modélisation :

① les effets de rotation de la balle sur le mouvement sont négligés (service « à plat ») ;

② la trajectoire de la balle se trouve dans le plan vertical (O,x,y) ;

③ le vecteur vitesse initiale de la balle est horizontal ;

④ l’action de l’air est négligeable.

Donnée : Intensité du champ de pesanteur g = 9,81 m.s^-2.

Partie A : Établissement de l’équation de la trajectoire dans le cadre du modèle choisi

L’objectif de cette partie est de retrouver l’équation de la trajectoire de la balle de tennis obtenue en admettant que les quatre hypothèses précédentes sont valables.

A.1. On donne les coordonnées des conditions initiales :

position de la balle frappée au service $B \begin{pmatrix} 0 \\ H \end{pmatrix}$ ;
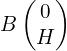vecteur vitesse initiale de la balle lors de la frappe $\overrightarrow{v_0} \begin{pmatrix} v_0 \\ 0 \end{pmatrix}$

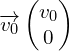
A.1.1. Par application d’une des lois de Newton, à énoncer, déterminer les composantes du vecteur accélération 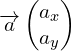$\overrightarrow{a} \begin{pmatrix} a_x \\ a_y \end{pmatrix}$ du centre de masse G de la balle, au cours de son mouvement.

Réponse :

Système {balle}

Référentiel terrestre supposé galiléen

D’après la deuxième loi de newton :

$\sum_{}^{}\overrightarrow{F}_{ext}=m\overrightarrow{a}$

$\overrightarrow{P}=m\overrightarrow{a}$

$m\overrightarrow{g}=m\overrightarrow{a}$

$\overrightarrow{a}=\overrightarrow{g}$

$\overrightarrow{g} \begin{cases} 0 \\-g \end{cases}$

$\overrightarrow{a} \begin{cases} a_{x}(t)=0 \\a_{y}(t)=-g \end{cases}$

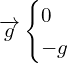
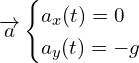
A.1.2. Déterminer les composantes du vecteur vitesse 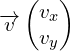$\overrightarrow{v} \begin{pmatrix} v_x \\ v_y \end{pmatrix}$ de G.

Réponse :

$\overrightarrow{a}=\frac{d \overrightarrow{v}}{dt}$

On intègre le système d’équation précédent :

$\overrightarrow{v} \begin{cases} v_{x}(t)=C_{1} \\v_{y}(t)=-gt+C_{2}\end{cases}$

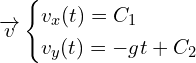
Pour trouver les constantes, on utilise $\overrightarrow{v_0}$ :

$\overrightarrow{v} \begin{cases} v_{0x}=v_{0} \\v_{0y}=0\end{cases}$

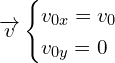
d’ou

$\overrightarrow{v} \begin{cases} v_{x}(t)=v_{0} \\v_{y}(t)=-gt\end{cases}$

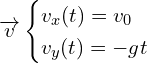
A.1.3. Déterminer les composantes du vecteur position 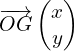$\overrightarrow{OG} \begin{pmatrix} x \\ y \end{pmatrix}$ de G.

Réponse :

$\overrightarrow{v}=\frac{d \overrightarrow{OG}}{dt}$

On intègre le système d’équation précédent :

$\overrightarrow{OG} \begin{cases} x(t)=v_{0} \times t +C_{3} \\y(t)=-\frac{1}{2}gt^2 + C_{4}\end{cases}$

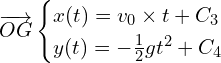
Pour trouver les constantes, on utilise $\overrightarrow{OM}_0$

$\overrightarrow{OG}_0 \begin{cases} x_0=0 \\y_0=H\end{cases}$

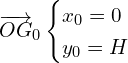
d’ou

$\overrightarrow{OG} \begin{cases} x(t)=v_{0}\times t \\y(t)=-\frac{1}{2}gt^2+ H\end{cases}$

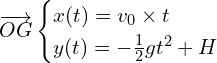
A.2. En déduire que l’équation de la trajectoire du centre de masse G de la balle établie dans le cadre du modèle choisi s’écrit :

$y(x)= - \frac{g}{2v_0^2}x^2+H$

Partie B : Influence de la vitesse initiale dans le cadre du modèle choisi

Selon les bases du modèle choisi, la vitesse initiale v₀ doit être comprise entre deux valeurs limites : elle doit être supérieure à une valeur minimum v_0min afin qu’elle franchisse juste le filet au point C et inférieure à une valeur maximum v_0max afin qu’elle retombe dans les limites autorisées au point D.

B.1. À partir de l’équation de la trajectoire du centre d’inertie de la balle, donner l’expression de la vitesse initiale v₀ en fonction de y(x), x, g et H.

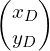B.2. Déterminer, à partir des documents fournis, les coordonnées $\begin{pmatrix} x_C \\ y_C \end{pmatrix}$ et $\begin{pmatrix} x_D \\ y_D \end{pmatrix}$ des points C et D.

B.3. Si la hauteur à laquelle la balle est frappée au service est H = 2,6 m, en déduire les valeurs v_0max et v_0min extrémales de la vitesse initiale de la balle pour que le service soit validé.

B.4. En réalité, la vitesse initiale mesurée lors du service est nettement supérieure aux vitesses calculées précédemment. Commenter.

Partie C : Étude énergétique

La quatrième et dernière hypothèse du modèle suppose que l’action de l’air est négligeable. À partir d’une étude énergétique du mouvement réel, dont les données figurent ci-dessous, montrer que cette hypothèse n’est pas vérifiée.

t (s)	0,00	0,03	0,06	0,09	0,12	0,15	0,18	0,21	0,24	0,27
y (m)	2,58	2,43	2,29	2,11	1,97	1,81	1,63	1,48	1,28	1,10
v (m⋅s^-1)	47,8	44,7	43,6	42,8	41,7	40,3	39,4	37,5	36,4	35,3

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti.