Bac Amérique du nord 2025 Sujet 2
Exercice 3 – (6 points) – Durée 1h03 – Calculatrice autorisée
Sujet n°25-PYCJ2AN1
Sujet et corrigé
La Mostiglass® est un vitrage en polycarbonate qui s’installe facilement devant les ouvertures et permet de réguler la température de l’air entrant, tout en protégeant des nuisibles à la façon d’une moustiquaire.
Source : d’après mostiglass.fr
L’objectif de cet exercice est d’expliquer la baisse de la température de l’intérieur d’une habitation par effet Venturi.
1. À la découverte de la Mostiglass®
La Mostiglass® est un vitrage transparent, perforé d’une multitude de fentes, comme l’indique la figure 1.

Pour mesurer précisément les dimensions des fentes de la Mostiglass®, on utilise la diffraction de la lumière.
Q.1. Donner une condition nécessaire à l’observation du phénomène de diffraction d’une onde lumineuse.
Pour observer un phénomène de diffraction d’une onde lumineuse il faut que l’ouverture soit du même ordre de grandeur ou plus petite que la longueur d’onde.
On réalise le montage suivant pour mesurer la largeur d’une fente de la Mostiglass® : un faisceau de lumière issu d’un laser de longueur d’onde l, traverse une perforation de la Mostiglass® assimilée à une fente de largeur l.
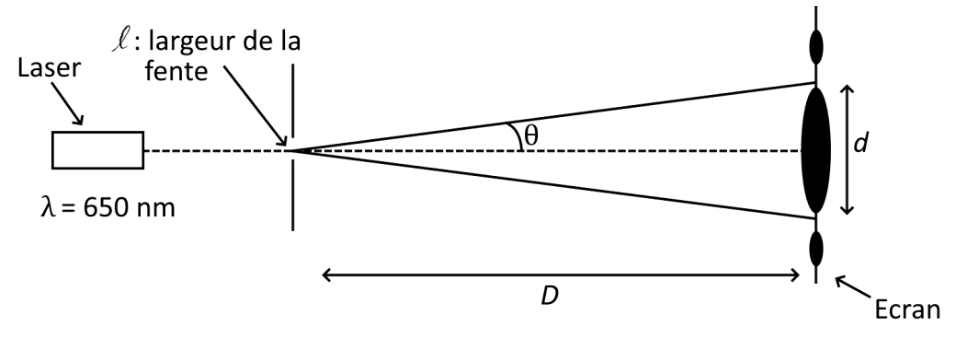
Figure 2. Schéma du montage expérimental vu du dessus
Données :
- Distance entre la fente et l’écran : D = 3,00 m avec u(D) = 0,01 m ;
- Longueur d’onde du laser utilisé : λ = 650 nm ;
- La mesure de la largeur de la tache centrale sur la figure de diffraction obtenue en éclairant une perforation est d = 6,0 mm avec u(d) = 0,5 mm.
Q.2. Donner la relation entre l’angle de diffraction θ, la longueur d’onde λ, et la largeur de la fente l.
$\theta=\frac{\lambda}{a}$
Ici $a=\ell$
$\theta=\frac{\lambda}{\ell}$
Q.3. Établir, en utilisant l’approximation des petits angles tan θ ≈ θ, la relation entre θ, la distance D entre la fente et l’écran, et d, la largeur de la tache centrale de diffraction. En déduire la relation suivante :
$$\frac{\lambda}{\ell} = \frac{d}{2D}$$
Lorsque $\theta$ est petit, on considère que$ \ tan\ \left(\theta\right)\approx\theta$ :
$$tan\ (\theta)\ =\frac{d}{2D}$$
$$\theta\ =\frac{d}{2D}$$
Or
$\theta=\frac{\lambda}{\ell}$
D’où
$$\frac{\lambda}{\ell}=\frac{d}{2D}$$
Q.4. En déduire la valeur de l, la largeur de la fente.
$$\frac{\ell}{\lambda}=\frac{2D}{d}$$
$$\ell=\frac{2D\lambda}{d}$$
$$\ell=\frac{2\times 3,00\times 650\times {10}^{-9}}{6,0\times {10}^{-3}}$$
$$\ell=6,5\times {10}^{-4}\ m$$
Données :
- Pour décider si le résultat d’une mesure est en accord avec une valeur de référence, on utilise le quotient $ \frac{\lvert x – x_{\mathrm{ref}} \rvert}{u(x)}$ avec x, la valeur mesurée ; xref la valeur de référence et u(x), l’incertitude-type associée à la valeur mesurée x ;
- L’incertitude-type sur la largeur l peut être obtenue grâce à la relation :
$$u(\ell)=\ell \times \sqrt{\left(\frac{u(d)}{d}\right)^2 + \left(\frac{u(D)}{D}\right)^2}$$
Q.5. Calculer l’incertitude-type u(l). Vérifier que le résultat de la mesure est compatible avec la valeur de référence l = 0,55 mm.
$$u(\ell)=\ell\times \sqrt{\left(\frac{u(d)}{d}\right)^2+\left(\frac{u(D)}{D}\right)^2}$$
$$u(\ell)=6,5\times {10}^{-4}\times \sqrt{\left(\frac{0,5}{6,0}\right)^2+\left(\frac{0,01}{3,00}\right)^2}$$
$$u(\ell)=6\times {10}^{-5}m$$
$$z=\left|\frac{\ell-\ell_{ref}}{u\left(\ell\right)}\right|$$
$$z=\left|\frac{6,5\times {10}^{-4}-0,55\times {10}^{-3}}{6\times {10}^{-5}}\right|$$
$$z=1,7$$
$z<2$ : le résultat de la mesure est compatible avec la valeur de référence $\ell = 0,55$ mm.
2. Étude de l’effet Venturi appliqué à la Mostiglass®
Les fentes présentes sur la Mostiglass® sont rétrécies : la surface d’entrée en contact avec l’air extérieur est supérieure à la surface de sortie en contact avec l’air intérieur. Ce rétrécissement est à l’origine de l’effet Venturi.
On réalise un montage (figure 3) dans lequel on injecte, à l’aide d’un sèche-cheveux, de l’air chaud dans un tunnel au centre duquel on place la Mostiglass®. Ce montage est schématisé figure 4.
On suit l’évolution de la température en fonction du temps dans le tunnel avant et après la Mostiglass® à l’aide de deux thermomètres reliés à une interface d’acquisition.

Figure 3. Photo du montage

Figure 4. Schéma du montage
L’expérience est réalisée sans la Mostiglass®. Les courbes obtenues sont représentées en figure 5a. T1 est la température d’entrée dans le tunnel, T2 est la température en sortie du tunnel. Puis la Mostiglass® est insérée au centre du tunnel, les courbes obtenues sont représentées en figure 5b.
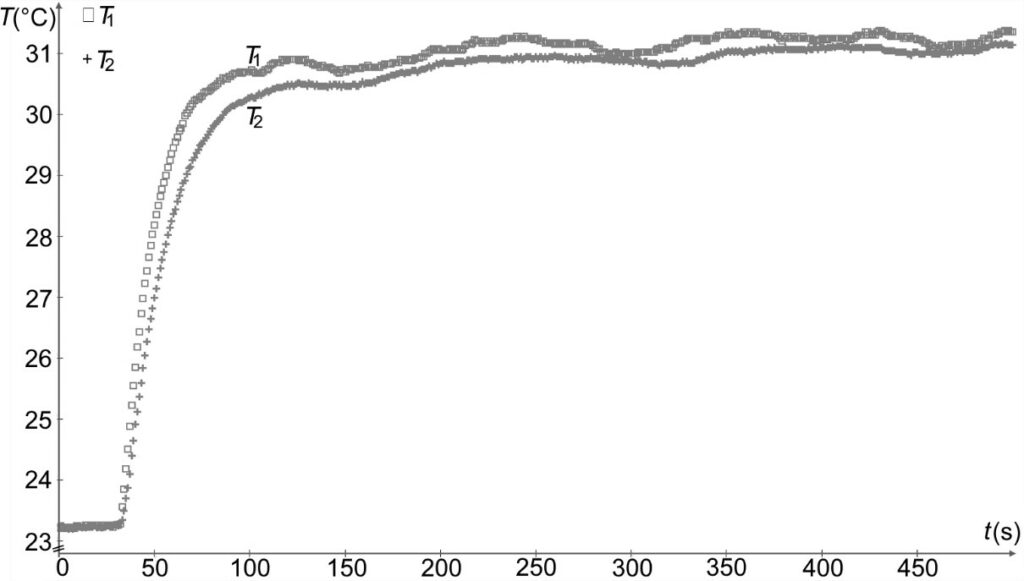
Figure 5a

Figure 5b
Q.6. Évaluer la valeur de la différence de température en régime permanent dans les deux études et confirmer l’intérêt de la Mostiglass®.
En régime permanent, sans la Mostiglass®, la valeur de la différence de température est proche de zéro.

En régime permanent, avec la Mostiglass®, la valeur de la différence de température est 32-27=5°C
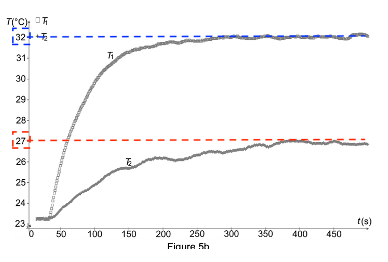
Ainsi, la Mostiglass® fait diminuer la température de l’air qui y passe de 5°C.
Données :
- La vitesse de l’air chaud à l’entrée du tunnel avant la Mostiglass®, a pour valeur v1 = 2,0 m·s-1.
- La masse volumique de l’air vaut 1,2 kg·m-3 ;
- Le tunnel utilisé a une section carrée de surface S0 = 4,0×10-2 m2 ;
- Les fentes de la plaque de Mostiglass® utilisée n’ont pas la même dimension en entrée et en sortie, donc :
- en entrée, en A : la surface ouverte est SA = 1,8 × 10-3 m² ;
- en sortie, en B : la surface ouverte est SB = 0,95 × 10-3 m² (Il y a un rétrécissement).
- Expression du débit volumique Dv : Dv = v × S avec v la vitesse d’écoulement du fluide et S la section traversée par le fluide ;
- Relation de Bernoulli pour l’écoulement d’un fluide parfait et incompressible en régime permanent entre deux points A et B situés sur une ligne d’écoulement horizontale :
$$ \frac{1}{2} \times \rho \times v_A^2 + p_A = \frac{1}{2} \times \rho \times v_B^2 + p_B $$
- avec ρ la masse volumique du fluide, vA et vB les vitesses d’écoulement en A et B et pA et pB les pressions en A et B ;
- T (kelvin) = 273 + T (°C).
- La relation entre la variation de pression (en Pa) et la variation de température (en K) est donnée par l’expression suivante :
$$\frac{\Delta T}{T} = \frac{\Delta P}{P} $$
- On prend comme référence la température à l’entrée de la Mostiglass® exprimée en kelvin et la pression pA égale à 1,01×105 Pa.
On considère l’air comme un fluide parfait et incompressible en écoulement permanent.
Q.7. Justifier, à l’aide de la conservation du débit volumique, que v1, la vitesse de l’air à l’entrée du tunnel, a la même valeur que v2, celle à la sortie du tunnel.
Conservation du débit volumique :
$$D_{V(1)}=D_{V(2)}$$
$$S_1\times v_1=S_2\times v_2$$
Or Le tunnel utilisé a une section carrée de surface $S_0 = 4,0\times {10}^{-2}$ m2 :
$S_1=S_2=S_0$
Ainsi :
$$v_1=v_2$$
La vitesse de l’air à l’entrée du tunnel, a la même valeur que $v_2$, celle à la sortie du tunnel.
Q.8. Calculer, à l’aide de la conservation du débit volumique, les valeurs des vitesses vA et vB, de l’air à l’entrée A et à la sortie B de la Mostiglass®.
$$D_{V(A)}=D_{V(1)}$$
$$S_A\times v_A=S_1\times v_1$$
$$v_A=\frac{S_1}{S_A}\times v_1$$
$$v_A=\frac{S_0}{S_A}\times v_1$$
$$v_A=\frac{4,0\times {10}^{-2}}{1,8\times {10}^{-3}}\times 2,0$$
$$v_A=44\ m.s^{-1}$$
$$v_B=\frac{S_0}{S_B}\times v_1$$
$$v_B=\frac{4,0\times {10}^{-2}}{0,95\times {10}^{-3}}\times 2,0$$
$$v_B=84\ m.s^{-1}$$
L’effet Venturi se produit lors du passage d’un fluide dans une conduite dont la section diminue. Il provoque une chute de pression.
Q.9. Montrer, en utilisant la relation de Bernoulli, que la Mostiglass® provoque bien un effet Venturi et évaluer l’ordre de grandeur de la baisse de température pour la comparer à celle de l’expérience. Commenter.
Le candidat est invité à prendre des initiatives et à présenter sa démarche. Toute démarche pertinente, même non aboutie, sera valorisée.
Relation de Bernoulli dans la conduite horizontale :
$$P+\frac{1}{2}\times \rho\times v^2+\rho\times g\times z=constante$$
$$P_B+\frac{1}{2}\times \rho\times v_B^2+\rho\times g\times z_B=P_A+\frac{1}{2}\times \rho\times v_A^2+\rho\times g\times z_A$$
Or $z_B=z_A$ car la conduite est horizontale.
$$P_B+\frac{1}{2}\times \rho\times v_B^2=P_A+\frac{1}{2}\times \rho\times v_A^2$$
$$P_B-P_A=\frac{1}{2}\times \rho\times v_A^2-\frac{1}{2}\times \rho\times v_B^2$$
$$∆P=12\times \rho\times v_A^2-v_B^2$$
$$∆P=12\times 1,2\times 44^2-84^2$$
$$∆P=-3,1\times 10^3\ Pa$$
La différence de pression est négative : l’air est aspiré.
Ainsi, la Mostiglass® provoque bien un effet Venturi.
$$ \frac{\Delta T}{T}=\frac{\Delta P}{P} $$
$$ \Delta T=\frac{\Delta P}{P}\times T $$
$$ \Delta T=\frac{-3,1\times 10^3}{1,01\times 10^5}\times (273+32) $$
$$ \Delta T=-9,4\ ^\circ K=-9,4\ ^\circ C $$
La diminution trouvée est supérieure à celle trouvée à la question Q.6 : le modèle appliqué n’est pas compatible avec l’expérience.
Cette différence peut s’expliquer par le fait que la relation de Bernoulli est pour l’écoulement d’un fluide parfait et incompressible or l’air est compressible.
