Mouvement d’une goutte d’encre dans une imprimante à jet d’encre

La Réunion 2023 sujet 2

Exercice 1 – (11 points) – Durée 1h56

Sujet n°23-PYCJ2LR1

EXERCICE I – MOUVEMENT D’UNE GOUTTE D’ENCRE DANS UNE IMPRIMANTE À JET D’ENCRE (11 points)

Développée dans les années 1970, la technique du jet d’encre continu est un procédé d’impression sans contact qui utilise la projection de gouttes d’encre liquide.

Immédiatement après avoir quitté la buse, les gouttes d’encre sont électrisées de manière contrôlée (figure 1). Elles passent ensuite entre les armatures d’un condensateur plan où règne un champ électrostatique. Les gouttes sont alors plus ou moins déviées vers le haut pour atteindre la feuille d’impression.

Les gouttes ne correspondant à aucun caractère imprimable ne sont pas électrisées si bien qu’elles ne subissent pas de déviation ; elles se dirigent alors vers le récupérateur et sont renvoyées vers les cartouches.

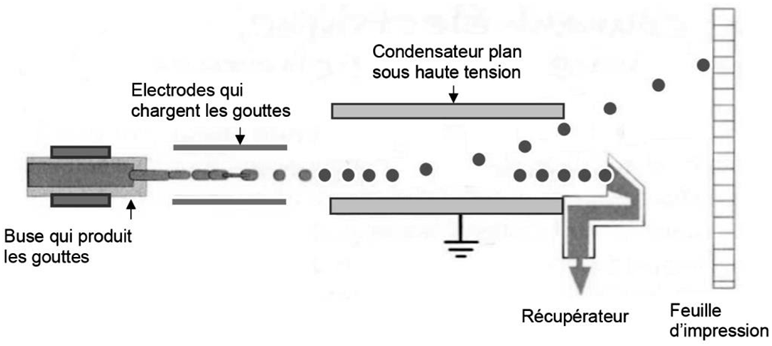
Figure 1 : Fonctionnement d’une imprimante à jet d’encre continu

Source : d’après « Vous avez dit physique ? » – K. Fadel – Dunod

PARTIE A : Modèle du condensateur plan

Un condensateur plan, de capacité 𝐶, est constitué de deux armatures conductrices, de surfaces 𝑆 identiques, planes en regard, parallèles entre elles. Elles sont séparées d’une distance 𝑑 par un matériau diélectrique (figure 2).

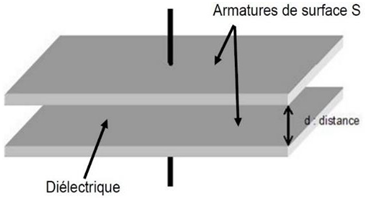
Figure 2 : Modèle du condensateur plan

La capacité 𝐶 dépend des caractéristiques du condensateur et on souhaite tester si elle respecte une relation de la forme

$c=k\times\frac{S}{d}$ (relation 1)

où 𝑘 est une constante.

Pour ce faire, on réalise un montage électrique dans lequel un condensateur plan de capacité variable est soumis à une tension continue 𝑈 = 1,50 V (figure 3).

Figure 3 : Schéma du circuit électrique réalisé

Au cours d’une première série de mesures, la distance entre les armatures est fixée à 𝑑 = 5 mm. En faisant varier la surface 𝑆 des armatures, on mesure la capacité 𝐶 du condensateur. Grâce aux mesures réalisées, on trace le graphe de la figure 4.

Une seconde série de mesures permet d’obtenir le graphe présenté en figure 5 : on mesure la capacité 𝐶 du condensateur en faisant varier la distance 𝑑 entre les armatures, leur surface 𝑆 étant fixée à 𝑆 = 200 mm².

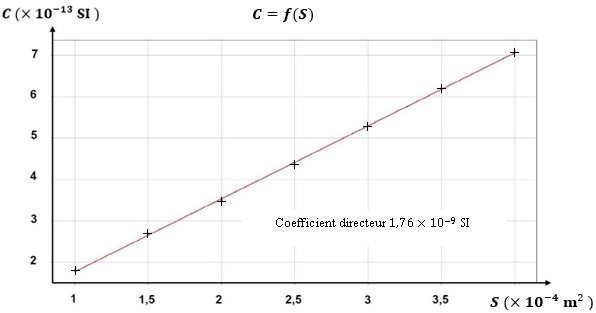
Figure 4 : Évolution de la capacité du condensateur plan en fonction de la surface de ses armatures

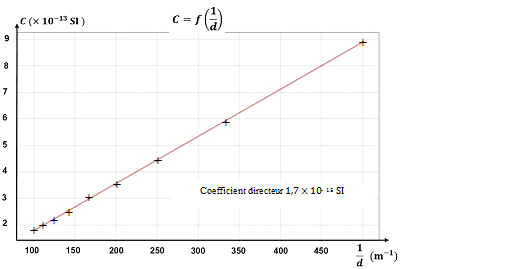
Figure 5 : Évolution de la capacité du condensateur plan en fonction de l’inverse de la distance entre ses armatures

A.1. Donner l’unité de la capacité d’un condensateur dans le système international (SI).

A.2. Montrer que les graphiques présentés en figures 4 et 5 respectent la relation 1.

PARTIE B : Mouvement d’une goutte d’encre électriquement chargée

Données :

Distance entre les armatures du condensateur plan : 𝑑 = 5,0 mm.
Longueur des armatures : 𝐿 = 20 mm.
Charge électrique du condensateur plan : 𝑞_C = 1,0 nC.
Distance entre le condensateur plan et la feuille d’impression : 𝐷 = 10 mm.
Volume d’une goutte d’encre : 𝑉 = 1,5 × 10⁻¹⁴ m³.
Masse volumique de l’encre : ρ = 9,5 × 10² kg ⋅ m⁻³.
Charge électrique d’une goutte d’encre : 𝑞 = − 2,0 × 10⁻¹³ C.
Intensité du champ de pesanteur terrestre : 𝑔 = 9,8 m ⋅ s⁻².
Tension constante appliquée entre les armatures : 𝑈 = 3,0 kV.
Valeur de la vitesse initiale de la goutte d’encre : 𝑣₀ = 30 m. s⁻¹.
Pour un condensateur plan, la valeur 𝐸 du champ électrostatique est reliée à la tension 𝑈 et à la distance 𝑑 qui sépare les armatures par la relation : $E=\frac{U}{d}$ .

B.1. Trajectoire d’une goutte d’encre électriquement chargée dans un champ électrique uniforme

Dans cette partie, on étudie le mouvement, dans le référentiel terrestre supposé galiléen, d’une goutte d’encre électriquement chargée assimilée à un point matériel M entre les plaques d’un condensateur plan de capacité 𝐶. Une tension constante 𝑈 est appliquée entre les armatures.

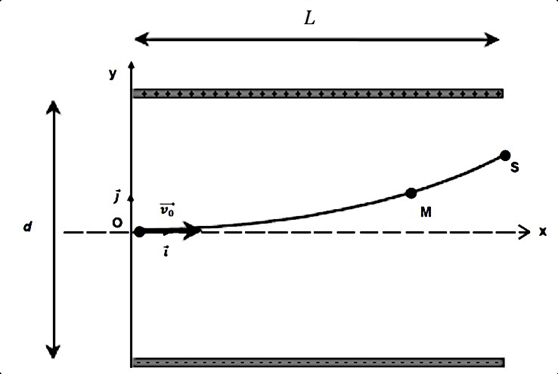
À l’instant 𝑡 = 0, la goutte arrive en un point O avec un vecteur vitesse initiale $\overrightarrow{v}_{0}$ parallèle aux armatures du condensateur plan (figure 6).

Lors de cette étude, on négligera tout type de frottement ainsi que la valeur du poids 𝑃 de la goutte d’encre devant la valeur de la force électrostatique 𝐹_𝑒 subie par la goutte.

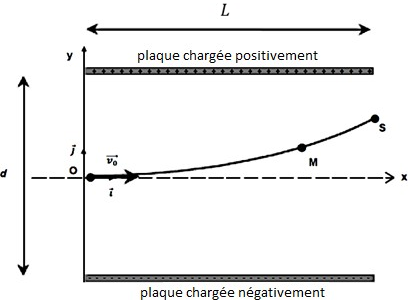
Figure 6 : Trajectoire de la goutte d’encre électriquement chargée

B.1.1. Vérifier quantitativement que l’hypothèse de négliger le poids de la goutte devant la force électrostatique est justifiée.

B.1.2. Compléter le schéma de l’ANNEXE À RENDRE AVEC LA COPIE (page 13/13) en représentant sans souci d’échelle le champ électrostatique $\overrightarrow{E}$ et la force électrostatique $\overrightarrow{F}_{e}$ que subit la goutte d’encre au point M. Justifier l’orientation de chacun des vecteurs.

B.1.3. Déterminer la valeur de la capacité 𝐶 du condensateur plan de charge 𝑞_C soumis à la tension électrique 𝑈.

B.1.4.1. Établir les équations horaires 𝑥(𝑡) et 𝑦(𝑡) du mouvement de la goutte d’encre.

B.1.4.2. En déduire que la trajectoire de la goutte d’encre au sein du condensateur plan s’écrit :

$y(x)=-\frac{q\times U}{2 \times m \times d \times v^{2}_0} \times x^{2}$

B.1.4.3.Donner alors l’expression de l’ordonnée 𝑦_𝑆 de la goutte à la sortie S du condensateur.

B.2. Impact de la goutte d’encre sur la feuille

À la sortie du condensateur plan, la goutte d’encre n’est soumise à aucune force (on néglige son poids). Elle acquiert alors un mouvement rectiligne uniforme jusqu’à la feuille de papier située à la distance 𝐷 du condensateur plan. Le point d’impact de la goutte sur la feuille se situe à l’ordonnée 𝑦 = O’Y avec O’ situé au centre de la feuille. La trajectoire rectiligne suivie par la goutte fait avec l’axe (𝑂𝑥) un angle a et intercepte l’axe au point I, milieu de OH (figure 7).

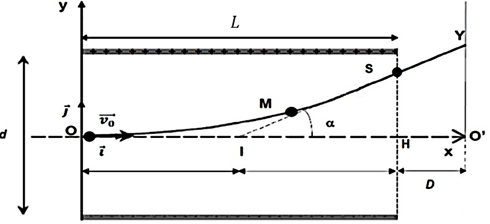
Figure 7 : Du condensateur plan à la feuille d’impression

B.2.1. Justifier que la goutte suit un mouvement rectiligne uniforme entre le condensateur plan et la feuille.

B.2.2.1. Exprimer tan a en fonction de O’Y et O’I d’une part et en fonction de SH et HI d’autre part.

B.2.2.2. En déduire que l’ordonnée 𝑌 du point d’impact de la goutte d’encre sur la feuille a pour expression :

$Y=-\frac{q\times U \times L}{2 \times m \times d \times v^{2}_0} \times \left ( \frac{L}{2}+D \right )$

B.2.2.3. Déterminer dans quelle zone de la feuille, c’est-à-dire zone 1, 2 ou 3 de la figure 8, la goutte va se déposer.

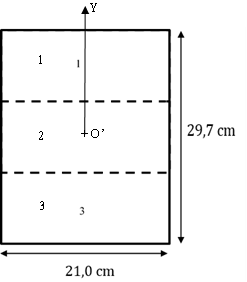
Figure 8 : Les différentes zones d’une feuille A4 (les trois zones sont de même dimension)

ANNEXE À RENDRE AVEC LA COPIE (même non complétée)

EXERCICE 1 – Question B.1.2