Nos oreilles on y tient !

Polynésie 2022 Sujet 2

Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 22-PYCJ2P01

Mots-clés : intensité sonore ; niveau d’intensité sonore ; atténuation

Le niveau d’intensité sonore est exprimé en décibels. L’échelle va de 0 à 120 dB. La limite de nocivité est située à 85 dB. Au-dessous, aucun risque auditif. Au-dessus, la nocivité augmente avec le niveau. On trouve des valeurs supérieures à 90 dB dans la vie professionnelle, les activités de loisirs (fêtes, sports mécaniques) et la musique.

D’après http://www.journee-audition.org/pdf/nos-oreilles.pdf

On peut lire dans un guide d’information de la journée nationale de l’audition l’affirmation suivante : « vous êtes exposé à 85dB et plus si, dans une file de voiture, votre voisin entend votre autoradio toutes vitres fermées. »

L’objectif de cet exercice est de vérifier l’affirmation du guide d’information.

Donnée :

Le niveau d’intensité sonore L est lié à l’intensité sonore I par la relation :

$L= 10 \times log \left (\frac{I}{I_0}\right)$

avec I_o l’intensité sonore de référence en watt par mètre carré, L en décibels et I en watt par mètre carré.

Étude du son perçu par les conducteurs de deux voitures ayant les fenêtres baissées.

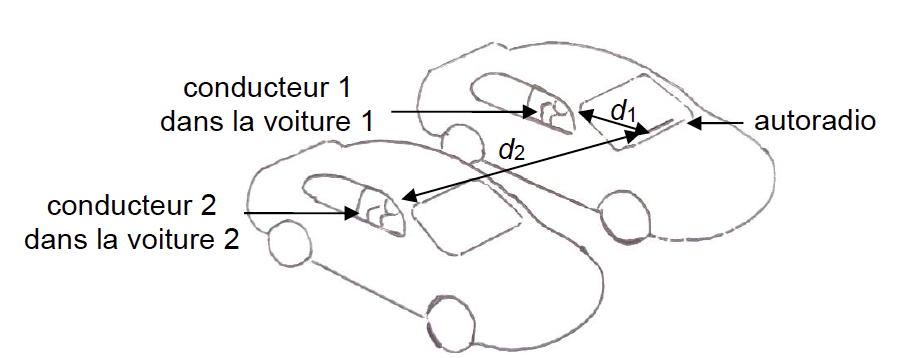
Figure 1. Schéma représentant les deux voitures côte à côte.

Dans la voiture 1, le conducteur 1 allume son autoradio. L’oreille du conducteur 1 est située à une distance d₁ égale à 1,0 m de l’autoradio. Les fenêtres de la voiture sont baissées.

Dans la voiture 2, les fenêtres sont également baissées. L’oreille du conducteur 2 est située à une distance d₂ égale à 3,1 m de l’autoradio de la première voiture.

Dans cette première partie, on considérera que l’atténuation de l’onde sonore ne dépend que de la distance entre la source et le récepteur et que la source est ponctuelle.

Donnée :

Dans le modèle de l’atténuation géométrique et pour une source ponctuelle, l’intensité sonore I perçue à une distance d de la source est reliée à la puissance sonore P de cette source par la relation :

$I= \frac{P}{4 \pi d^2}$

Avec P la puissance de l’onde sonore en watt et d la distance à la source en mètre.

1. Exprimer l’intensité sonore I₁ reçue par le conducteur 1 en fonction de la puissance sonore P et de d₁ puis exprimer l’intensité sonore I₂ reçue par le conducteur 2 en fonction de P et de d₂.

2. À l’aide des données, montrer que l’atténuation géométrique A_géo du conducteur 1 au conducteur 2 en décibels peut s’exprimer sous la forme :

$A{géo}= 10 \times log \left (\frac{I_1}{I_2}\right)$

3. Vérifier que l’atténuation A_géo est égale à 9,8 dB.

Dans la suite, la valeur de l’atténuation A_géo sera arrondie à 10 dB.

En plaçant son smartphone près de son oreille et en utilisant une application sonomètre, le conducteur 1 mesure un niveau d’intensité sonore L₁ = (80±3) dB. Le conducteur 2 fait de même et mesure un niveau d’intensité sonore L₂ = (68±3) dB.

4. À l’aide des mesures précédentes, calculer la valeur expérimentale A_mesure de l’atténuation géométrique.

Données :

L’incertitude-type u(A_mesure) sur la grandeur A_mesure peut se calculer à partir de la relation :

$u(A_{mesure})= \sqrt{u(L_1)^2+u(L_2)^2$

avec u(x) désigne l’incertitude-type associée à la grandeur x

Le z-score noté z, correspond à l’écart entre le résultat de la mesure x et la valeur de référence xref évalué en nombre d’incertitude-type.

$z= \frac{\lvert x-x_{ref} \rvert }{u(x)}$

Si le z-score z est inférieur à 2 alors x et xref sont considérés compatibles.

5. Calculer l’incertitude-type de l’atténuation A_mesure.

6. Comparer, en utilisant le z-score, l’atténuation A_géo et l’atténuation mesurée A_mesure et conclure sur la compatibilité de ces deux valeurs.

Étude du son perçu par les conducteurs de deux voitures ayant les fenêtres fermées.

Dans cette partie, les deux conducteurs ferment entièrement leurs fenêtres et le conducteur 1 monte le volume de l’autoradio jusqu’à ce qu’il soit audible par le conducteur 2.

7. À l’atténuation géométrique A_géo s’ajoute l’atténuation due à la fermeture des deux fenêtres A_fenêtres. Choisir la nature de cette nouvelle atténuation parmi les deux propositions suivantes :

atténuation géométrique
atténuation par absorption

Données :

A_fenêtres= 18 dB (pour les deux fenêtres)
Le conducteur 2 mesure maintenant un niveau d’intensité sonore L^‘ égal à 63 dB.

8. Déterminer si le conducteur 1 est exposé à un niveau d’intensité sonore supérieur à la limite de nocivité.