Observation de la planète Mars

Métropole 2022 Sujet 2

Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée

Sujet n° 22-PYCJ2ME1

[latexpage]

La planète Mars est une planète du système solaire au cœur de multiples projets scientifiques internationaux destinés à mieux connaitre son sol et son histoire.

Les objectifs de l’exercice sont de déterminer quelques caractéristiques de la planète Mars à partir :

de la mesure de l’angle sous lequel elle est vue par un observateur terrestre ;
de l’observation de Phobos, l’un de ses satellites naturels.

Données :

angle θ, exprimé en radian, sous lequel la planète Mars est vue par un observateur terrestre :

on se place dans le cadre de l’approximation des petits angles (θ << 1 rad) :
– tan (θ) ≈ θ avec θ en rad ;
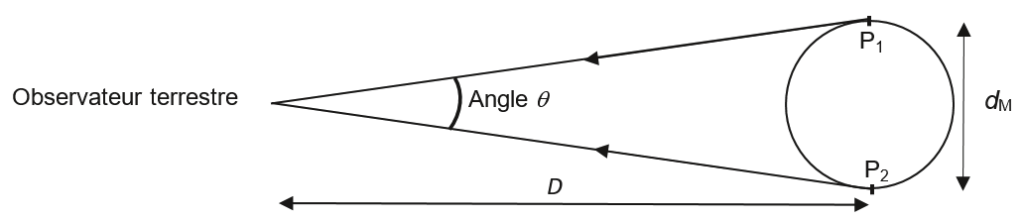
– la distance Terre-Mars, notée D , étant suffisamment grande devant le diamètre de Mars, noté d_M , l’angle θ (en rad) a pour expression :

$\theta \approx \frac{d_M}{D} $

pouvoir séparateur de l’œil humain : il correspond à l’angle minimal, noté e, au-dessus duquel l’œil humain peut différencier deux points. Il a pour valeur e = 2,9×10^–4 rad ;
constante de gravitation universelle : G = 6,67×10^–11 m³·kg^–1·s^–2 ;
diamètre moyen de référence de la planète Mars : d_Ref = 6,78×10³ km ;
rayon de l’orbite, supposée circulaire, de Mars autour du Soleil : r_SM = 2,28×10⁸ km ;
masse de la Terre : M_T = 5,97×10²⁴ kg.

1. Observation de Mars avec une lunette astronomique

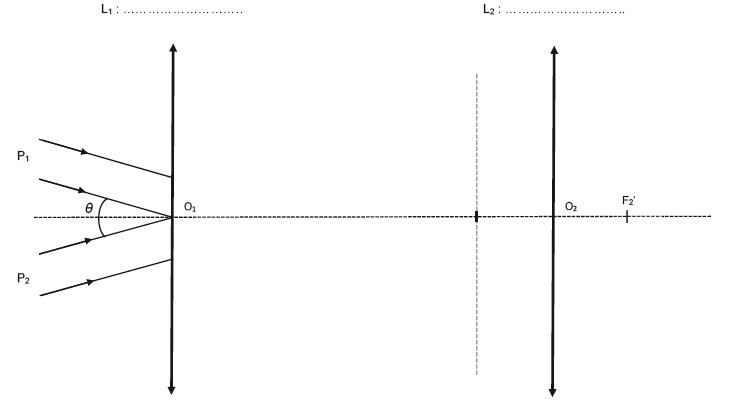
On peut observer la planète Mars avec une lunette astronomique afocale composée de deux lentilles minces convergentes L₁ et L₂ de distances focales respectives f₁’ = 900 mm et f₂’ = 20 mm. Le schéma donné en ANNEXE À RENDRE AVEC LA COPIE représente des rayons lumineux provenant des deux points de Mars P₁ et P₂.

Ces deux points sont :

situés à la surface de Mars ;
- supposés à l’infini ;
- diamétralement opposés ;
- écartés d’un angle θ correspondant à l’angle sous lequel la planète Mars est vue par un observateur terrestre ;
- observés depuis la surface de la Terre.

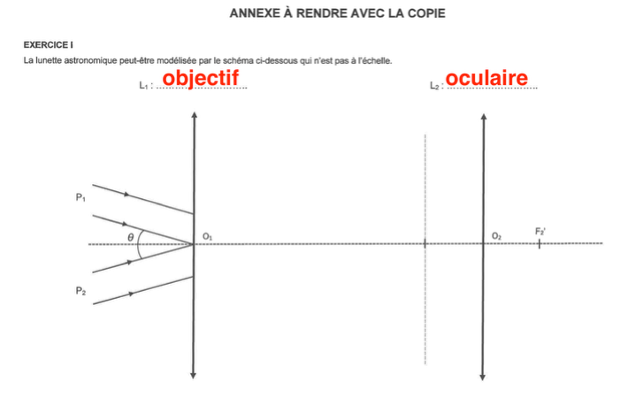
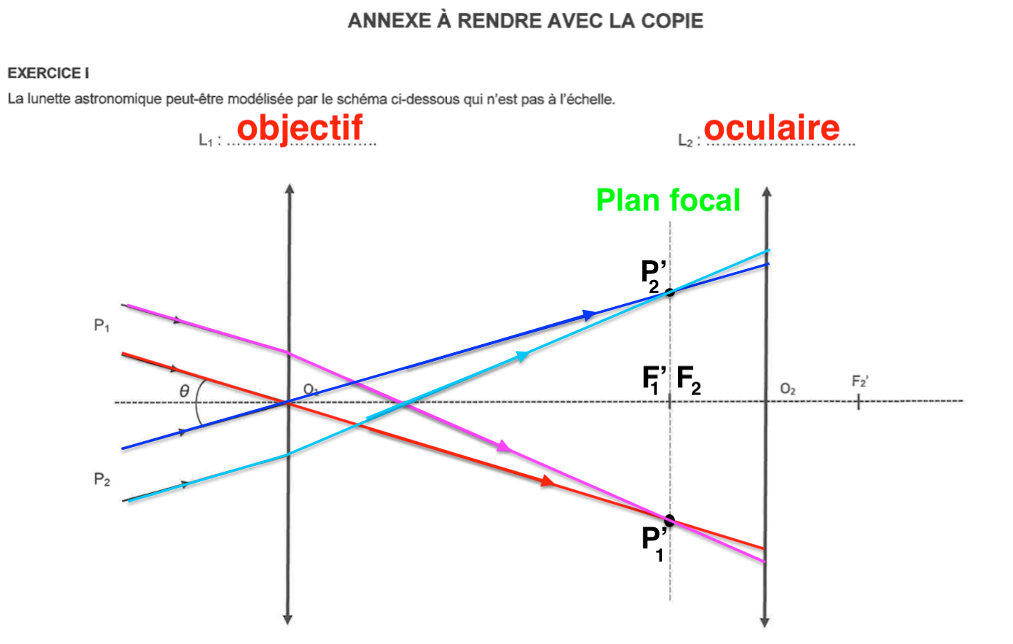
Q1. Indiquer sur le schéma en ANNEXE À RENDRE AVEC LA COPIE, au-dessus de la lentille correspondante, la lentille qui joue le rôle d’objectif et celle qui joue le rôle d’oculaire.

L₁ : l’objectif car c’est une lentille convergente possédant une grande distance focale. C’est la lentille placée vers l’objet

L₂ : l’oculaire car c’est une lentille convergente possédant une petite distance focale. C’est la lentille où on place l’œil.

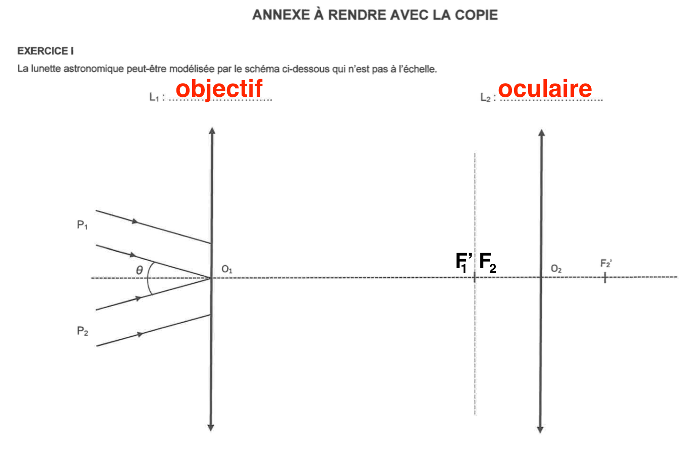
Q2. Citer la propriété caractéristique d’une lunette astronomique dite « afocale ». Donner la position du foyer objet F₂ de la lentille L₂ par rapport à celle du foyer image F₁’ de la lentille L₁ de cette lunette. Placer ces deux points sur le schéma en ANNEXE À RENDRE AVEC LA COPIE.

Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.

Les deux foyers $F_1^\prime$ et $F_2$ sont confondus.

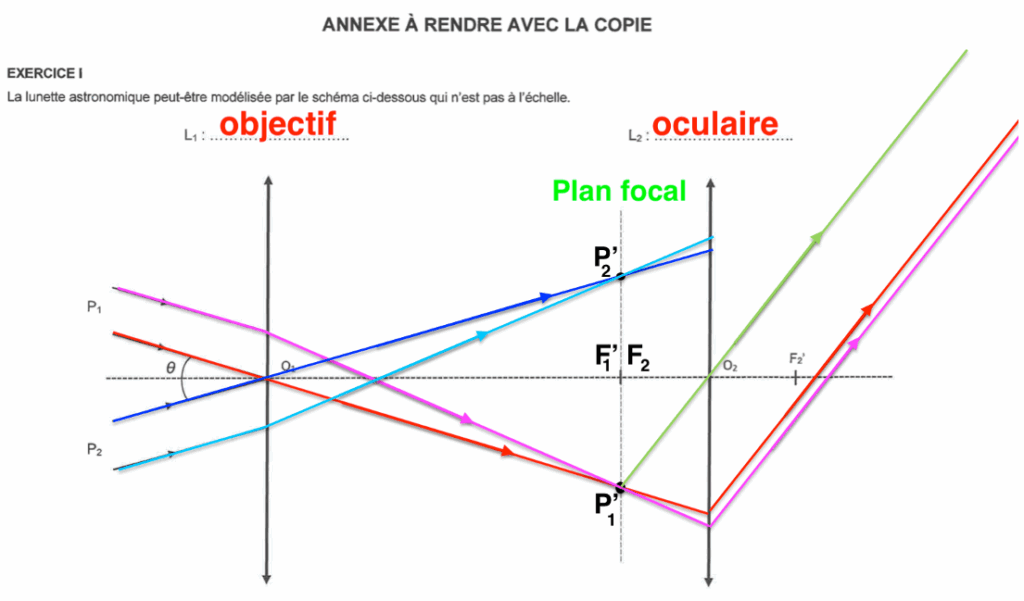
Q3. Tracer sur le schéma en ANNEXE À RENDRE AVEC LA COPIE la marche des rayons lumineux issus des points P₁ et P₂ de Mars :

à travers la lentille L₁ en faisant apparaître les images intermédiaires P₁’ et P₂’, des points P₁ et P₂ ;
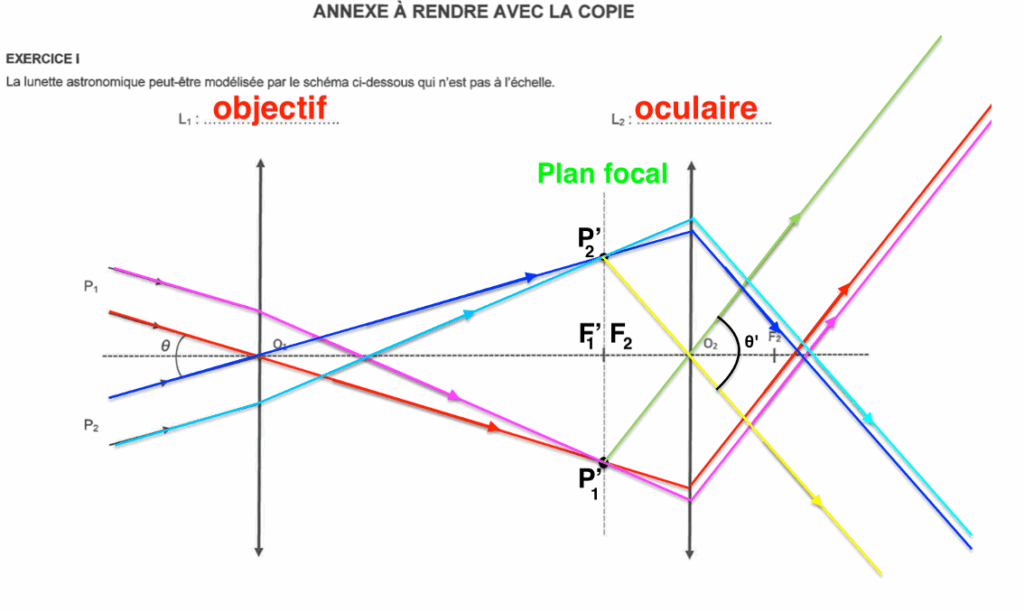
puis à travers la lentille L₂ en faisant apparaître l’angle θ ’ sous lequel la planète Mars est vue en sortie de la lunette.

Le rayon lumineux 3 issu de $\mathbf{P}_\mathbf{1}$ pénétrant dans la lunette par le centre optique $O_1$ de la lentille $L_1$ n’est pas dévié.

Position de $\ \mathbf{P}_\mathbf{1}^\prime$ image intermédiaire de $\mathbf{P}_\mathbf{1}$ : Comme $\mathbf{P}_\mathbf{1}$ est à l’infini, son image $\mathbf{P}_\mathbf{1}^\prime$ est dans le plan focal image de l’objectif $L1$.

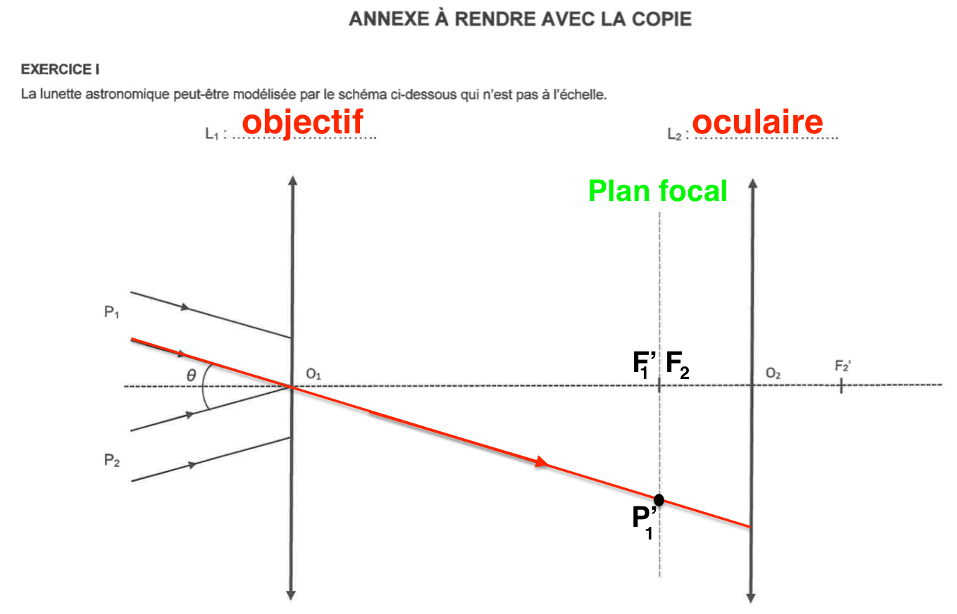
L’autre rayon lumineux issu $\mathbf{P}_\mathbf{1}$ est dévié vers $\mathbf{P}_\mathbf{1}^\prime$.

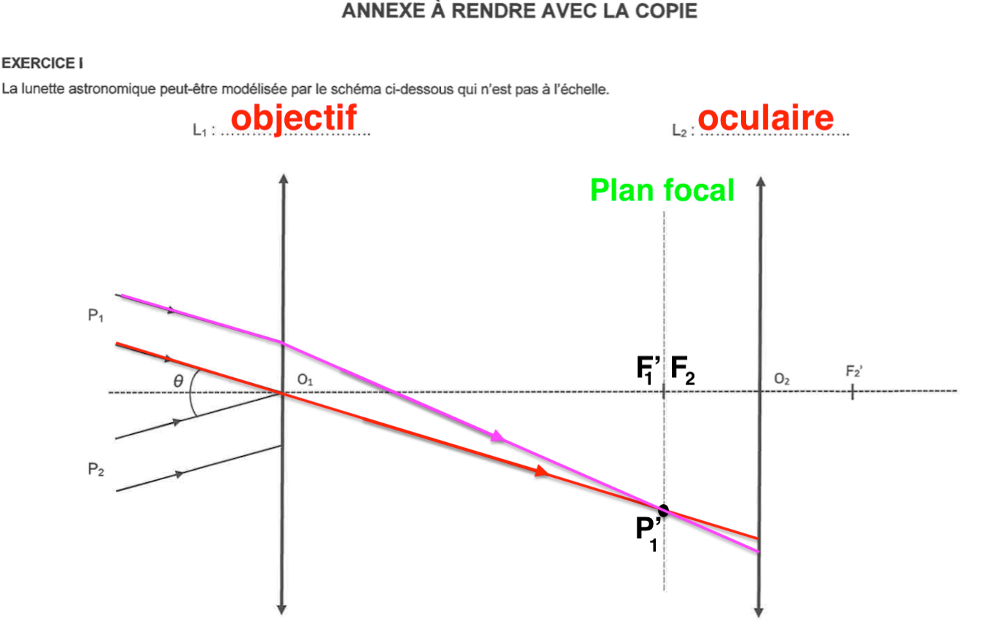
Même démarche pour $P_2$

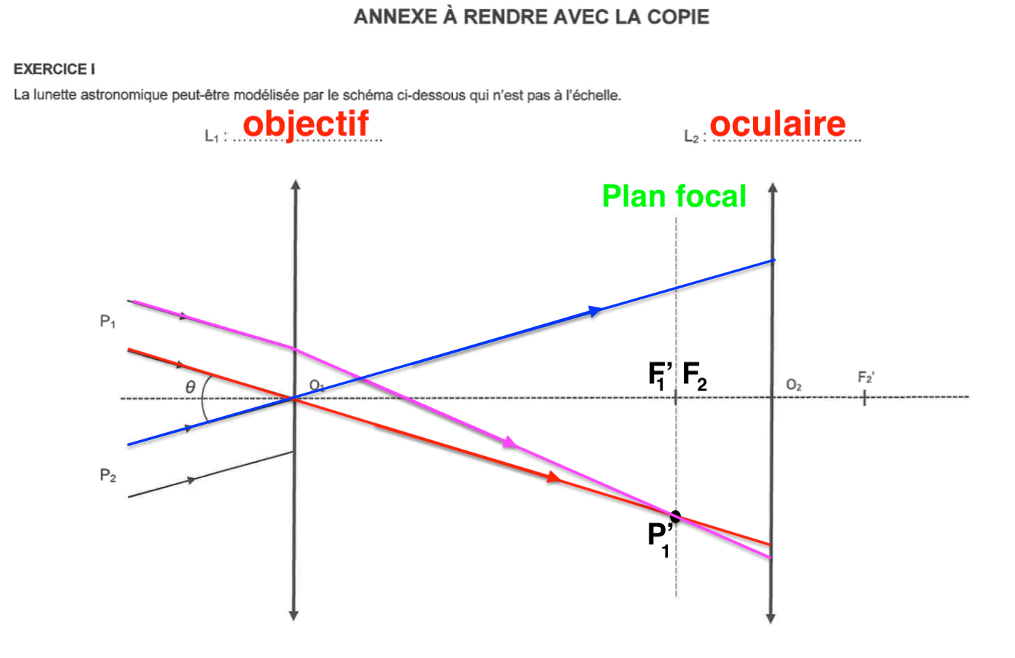
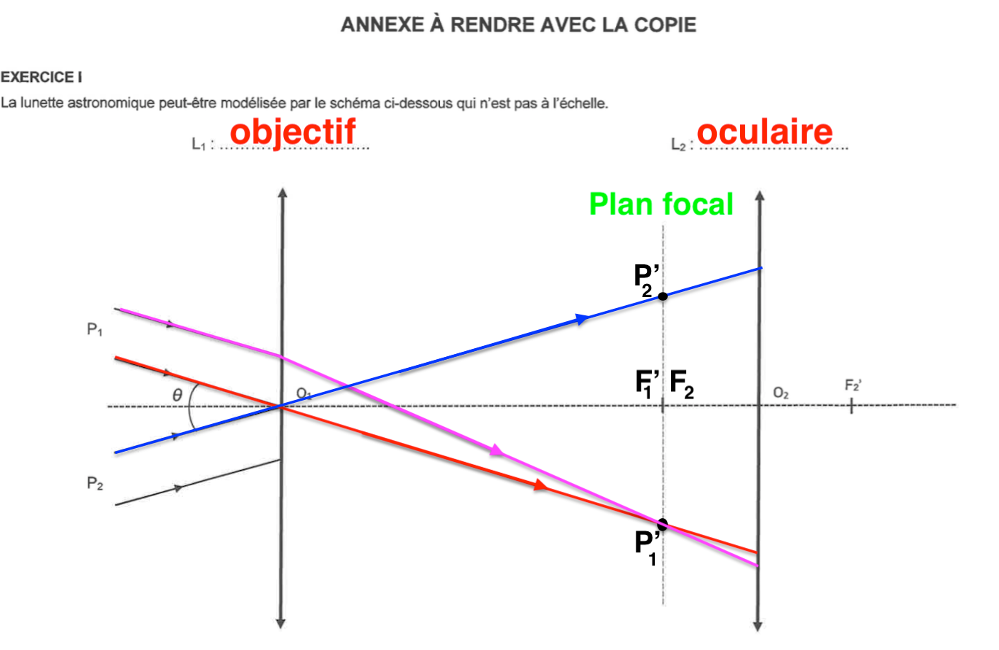
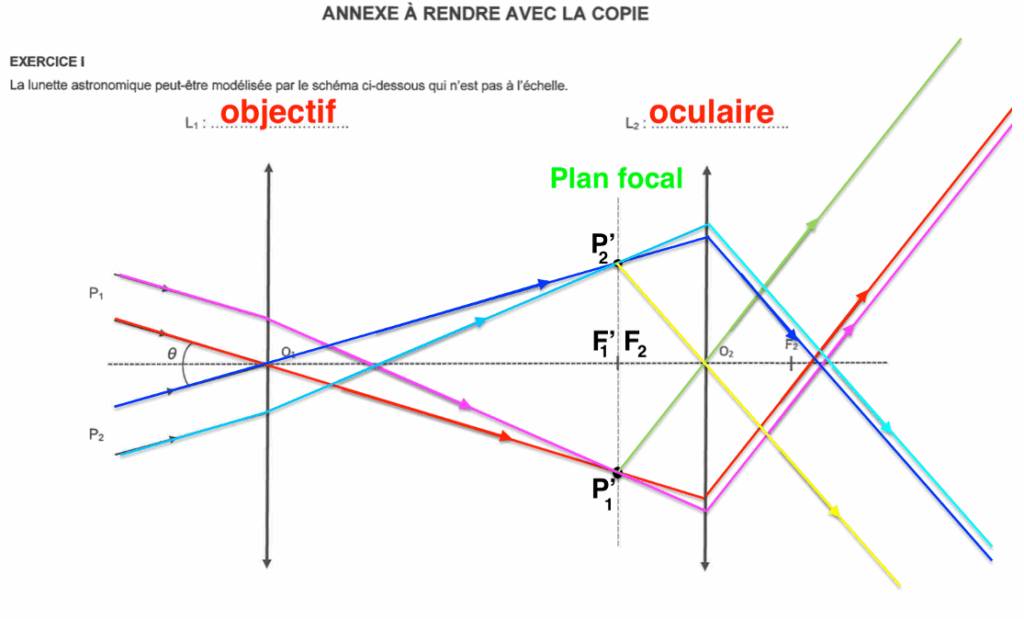
Pour les rayons émergeants de la lentille $L2$ :

On trace un rayon issu de $\mathbf{P}_\mathbf{1}^\prime$ passant par $O_2$. Ce rayon ne sera pas dévié.

De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi les rayons émergeants de la lentille $L_2$ issue de $\mathbf{P}_\mathbf{1}^\prime$ seront parallèles à ce rayon tracé.

Même démarche pour $P_2^\prime$

On place $\theta^\prime$

On admet que le grossissement de la lunette astronomique afocale s’exprime par la relation :

$G_{lunette}= \frac{f_1′}{f_2′} $

Q4. Calculer la valeur du grossissement Glunette de la lunette utilisée.

$$G=\frac{f_1^\prime}{f_2^\prime}$$

$$G=\frac{900}{20}$$

$$G=45$$

En janvier 2021, l’angle sous lequel la planète Mars est vue par un observateur terrestre à l’œil nu était de θ = 4,9×10^–5 rad. Cet observateur voit alors un point lumineux.

Q5. Justifier cette observation.

$$\theta=4,9\times 10^{-5}\ \text{rad}$$

$$\varepsilon=2,9\times 10^{-4}\ \text{rad}$$

$\theta<\varepsilon$

L’œil ne peut donc différencier deux points : l’observateur voit alors un point lumineux.

Q6. Indiquer ce qu’il observe en utilisant la lunette astronomique précédente. Justifier par un calcul.

$$G=\frac{\theta^\prime}{\theta}$$

$$\frac{\theta^\prime}{\theta}=G$$

$$\theta^\prime=G\times \theta$$

$$\theta^\prime=45\times 4,9\times 10^{-5}$$

$$\theta^\prime=2,2\times 10^{-3}\ \text{rad}$$

$\theta^\prime>\varepsilon$

L’œil peut donc différencier deux points.

2. Détermination du diamètre de Mars

À l’aide des mesures effectuées en début de chaque mois avec la lunette astronomique, on détermine l’angle θ sous lequel la planète Mars est vue par un observateur terrestre à partir de janvier 2018.

Lorsque Mars n’est pas visible, on utilise des données simulées.

Les valeurs de l’angle θ sont représentées en fonction du temps t sur la figure 1. La date t = 0 correspond au 1^er janvier 2018.

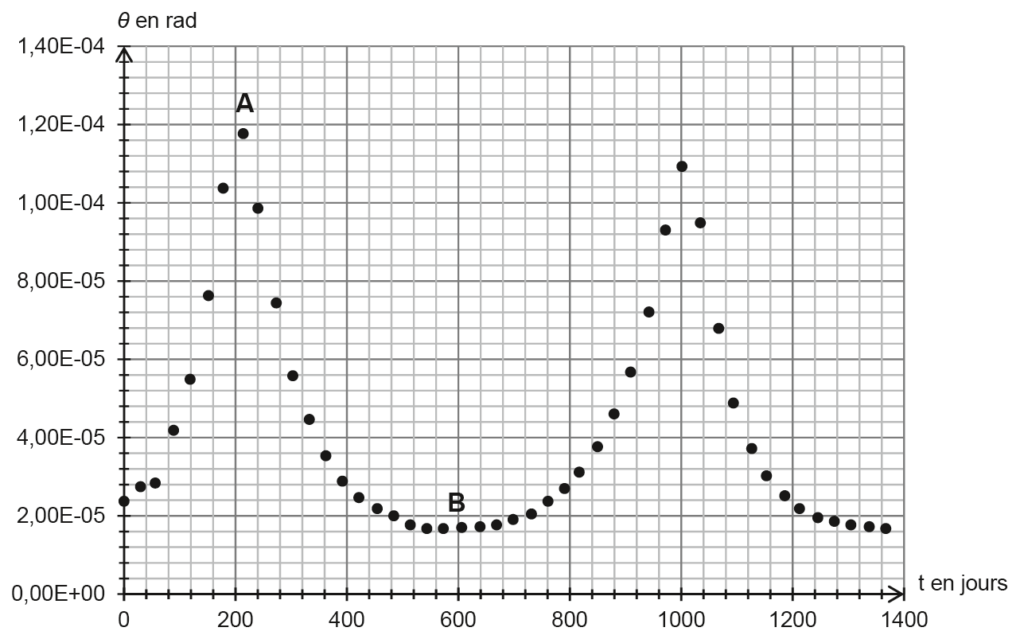
Figure 1. Évolution de l’angle θ sous lequel la planète Mars est vue par un observateur terrestre en fonction du temps t

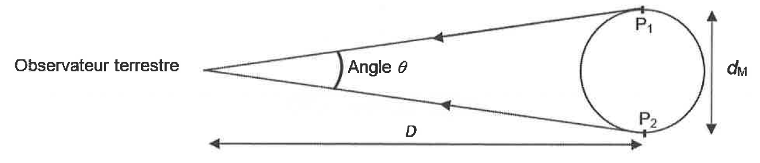
Le schéma présenté en figure 2 montre les deux positions extrêmes de Mars par rapport à la Terre ainsi que les angles θ1 et θ2 sous lesquels la planète Mars est vue par un observateur terrestre pour ces deux positions.

Figure 2. Schéma des positions relatives de Mars par rapport à la Terre (échelle non respectée)

Q7. Associer, en expliquant votre démarche, les angles θ₁ et θ₂ sous lesquels la planète Mars est vue par un observateur terrestre aux points A et B de la figure 1. En déduire les valeurs de θ₁ et θ₂.

$\theta_1$ l’angle maximal car Mars est au plus près de la terre

$\theta_2$ l’angle minimal car Mars est au plus loin de la terre

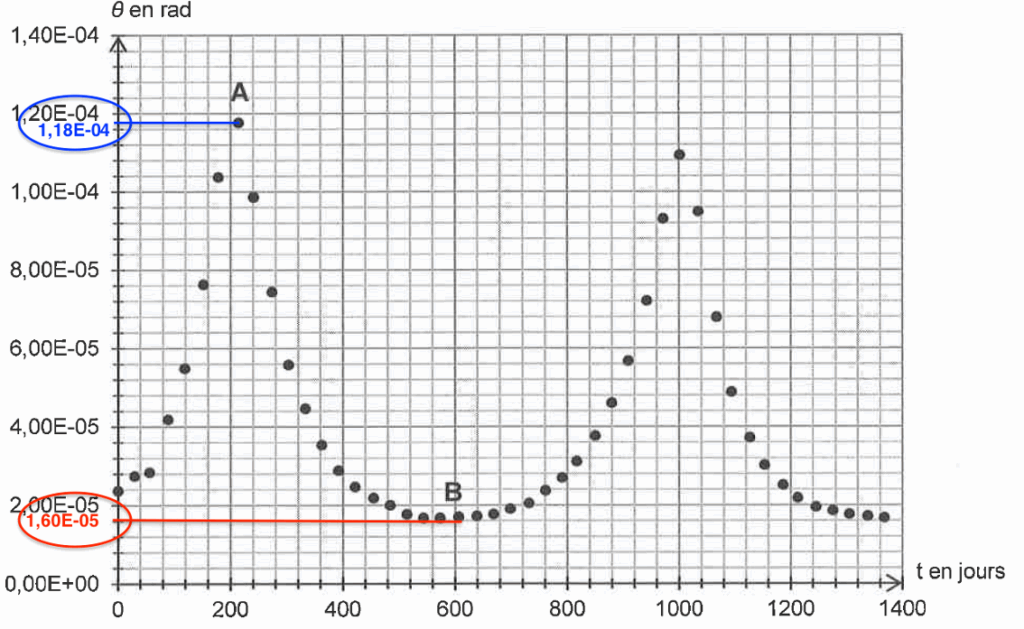
$$\theta_1=1,18\times 10^{-4}\ \text{rad}$$

$$\theta_2=1,60\times 10^{-5}\ \text{rad}$$

Q8. En utilisant la figure 2, montrer que l’expression du diamètre d_M de la planète Mars s’exprime de la façon suivante :

$d_{M}= \frac{2r_{SM}}{\left (\frac{1}{\theta_1}+\frac{1}{\theta_2}\right)} $

$$\tan\left(\theta\right)\approx \theta=\frac{d_M}{D}$$

$$\theta=\frac{d_M}{D}$$

$$\theta_1=\frac{d_M}{D_1}$$

$$D_1=\frac{d_M}{\theta_1}$$

$$\theta_2=\frac{d_M}{D_2}$$

$$D_2=\frac{d_M}{\theta_2}$$

Or, graphiquement $D_1+D_2=2r_{SM}$

D’ou

$$D_1+D_2=2r_{SM}$$

$$\frac{d_M}{\theta_1}+\frac{d_M}{\theta_2}=2r_{SM}$$

$$d_M\left(\frac{1}{\theta_1}+\frac{1}{\theta_2}\right)=2r_{SM}$$

$$d_M=\frac{2r_{SM}}{\left(\frac{1}{\theta_1}+\frac{1}{\theta_2}\right)}$$

Q9. Calculer la valeur du diamètre d_M de la planète Mars. Commenter.

$$d_M=\frac{2r_{SM}}{\left(\frac{1}{\theta_1}+\frac{1}{\theta_2}\right)}$$

$$d_M=\frac{2\times 2,2\times 10^8}{\left(\frac{1}{1,18\times 10^{-4}}+\frac{1}{1,60\times 10^{-5}}\right)}$$

$$d_M=6,2\times 10^3\ \text{km}$$

$$d_{ref}=6,78\times 10^3\ \text{km}$$

Les deux valeurs sont du même ordre de grandeur.

3. Détermination de la masse de Mars

La planète Mars, que l’on peut assimiler à une sphère de diamètre d_M, possède une masse M_M environ dix fois moins grande que celle de la Terre.

La masse M_M de Mars peut être déterminée par l’observation de Phobos, l’un des satellites naturels de la planète et par l’utilisation des lois de Newton.

Ce satellite :

a une période de révolution T de 7 h 39 min autour de Mars ;
possède une trajectoire quasi-circulaire autour de Mars de rayon r_MP = 9,38×10³ km ;
n’est soumis qu’à la seule force de gravitation de Mars.

Q10. En utilisant une loi de Newton, établir que l’expression de la vitesse de Phobos sur son orbite circulaire autour de Mars est :

$v=\sqrt{ \frac{GM_{M}}{r_{MP}}} $

Réponse :

Système : Phobos

Référentiel : Marsocentrique supposé galiléen

D’après la 2^nd loi de Newton :

$\sum_{}^{}\overrightarrow{F_{ext}}=m\overrightarrow{a}$

$\overrightarrow{F}_{M/P}=m\overrightarrow{a}$

$G\times \frac{m\times M_{M}}{r_{MP}^2}\overrightarrow{n}=m\overrightarrow{a}$

$\overrightarrow{a}_{S}=G\times \frac{M_{M}}{r_{MP}^2}\overrightarrow{n}$

Or, pour un mouvement circulaire, dans la base de Frenet, le vecteur accélération est de la forme :

$\vec{a}_{S}=\frac{v_{S}^2}{r_{MP}}\vec{n}+\frac{dv_{S}}{dt}\vec{t}$

L’accélération étant unique, par identification :

$\frac{v_{S}^2}{r_{MP}}=G\ \times \frac{M_M}{r_{MP}^2}$

donc

$v_{S}=\sqrt{\frac{G\times M_{M}}{r_{MP}}}$

Q11. Déterminer la valeur de la masse M_M de Mars. Commenter.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

La période de révolution est :

$$T=\frac{circonference}{vitesse}$$

$$T=\frac{2\pi R}{v}$$

$$T=\frac{2\pi r_{MP}}{\sqrt{\ \frac{G\times M_M}{r_{MP}}}}$$

$$T=2\pi r_{MP}\sqrt{\frac{r_{MP}}{G\times M_M}}$$

$$T^2=4\pi^2 r_{MP}^2\frac{r_{MP}}{G\times M_M}$$

$$T^2=\frac{4\pi^2 r_{MP}^3}{G\times M_M}$$

$$M_M=\frac{4\pi^2 r_{MP}^3}{G\times T^2}$$

$$M_M=\frac{4\pi^2\left(9,38\times 10^3\times 10^3\right)^3}{6,67\times 10^{-11}\times \left(7\times 60\times 60+39\times 60\right)^2}$$

$$M_M=6,44\times 10^{23}\ \text{Kg}$$

$$M_T=5,97\times 10^{24}\ \text{Kg}$$

$$\frac{M_T}{M_M}=\frac{5,97\times 10^{24}}{6,44\times 10^{23}}$$

$$\frac{M_T}{M_M}=9,3$$

On retrouve la phrase du texte : la planète mars possède une masse environ dix fois moins grande que celle de la Terre.

ANNEXE À RENDRE AVEC LA COPIE

La lunette astronomique peut-être modélisée par le schéma ci-dessous qui n’est pas à l’échelle.