Bac Asie 2024 Sujet 1
Exercice 2 – (6 points) – Durée 1h03 – Calculatrice autorisée
Sujet n°24-PYCJ1JA1
Sujet et corrigé
Exercice 2 – Observation distante (6 points)
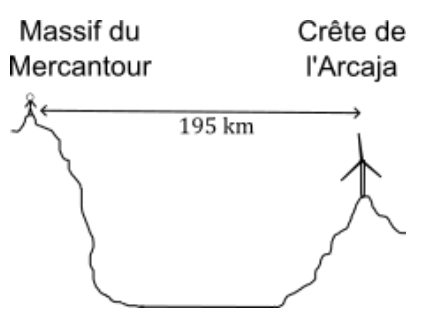
Par temps clair, il est possible d’apercevoir la crête de l’Arcaja (nord de la Corse) depuis le massif du Mercantour (sud de la France) alors qu’ils sont séparés d’environ 195 km.
Cet exercice étudie les conditions requises pour distinguer les pales d’une éolienne située sur la crête de l’Arcaja depuis le massif du Mercantour. Pour cela, on envisage d’abord une observation à l’œil nu, puis avec une lunette afocale.
Données :
- Distance entre le lieu d’observation et la crête de l’Arcaja : 𝐷 = 195 km
- Longueur d’une pale d’éolienne : 𝐿 = 44 m
Discernabilité à l’œil nu
Dans un premier temps, on s’intéresse à la possibilité de discerner les pales de l’éolienne à l’œil nu.
La capacité à distinguer à l’œil nu des détails sur des objets éloignés est caractérisée par le pouvoir séparateur de l’œil. Noté 𝜀 et exprimé en radian, ce pouvoir séparateur correspond à l’angle minimal devant exister entre les rayons issus de deux objets A et B lorsqu’ils atteignent l’œil d’un observateur éloigné pour qu’il puisse distinguer A et B. En appelant 𝜃 l’angle entre ces rayons (voir le document 1), la règle est donc :
- Si 𝜃 > 𝜀, les points A et B sont perçus comme distincts (on perçoit l’extension de l’objet AB).
- Si 𝜃 < 𝜀, les points A et B sont perçus comme un point unique.
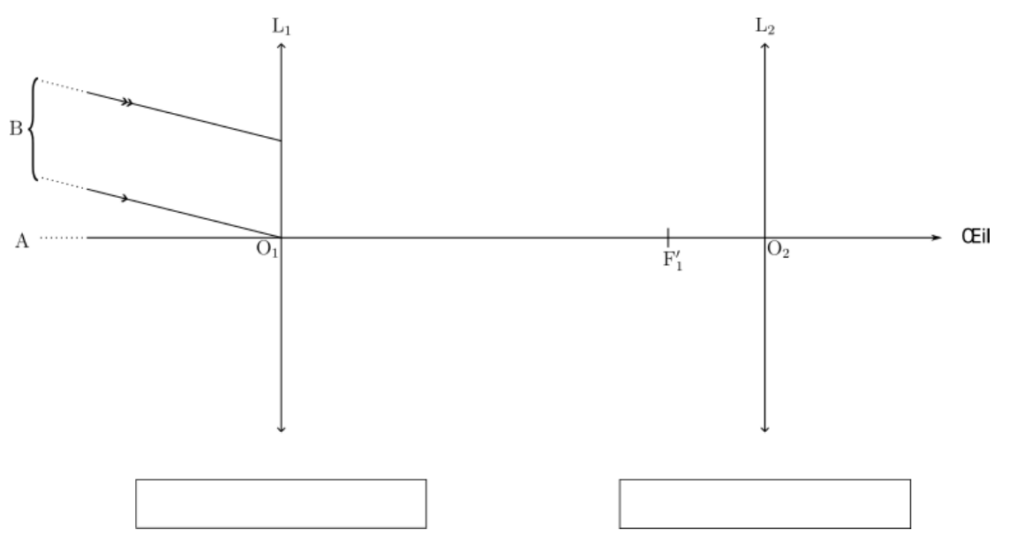
Document 1 – Observation à l’œil nu d’un objet distant

Données :
- Pouvoir séparateur de l’œil de l’observateur : 𝜀 = 3,0 × 10−4 rad
- Pour des angles très petits, exprimés en radian : tan 𝜃 ≈ 𝜃
Q1- Montrer que la valeur de l’angle 𝜃 lorsque l’observateur cherche à observer une pale de l’éolienne à l’œil nu est 2,3 × 10−4 rad.
Pour des angles très petits, exprimés en radian : tan 𝜃 ≈ 𝜃
$\theta \approx \tan \theta = \dfrac{\text{opposé}}{\text{adjacent}}$
$\theta=\dfrac{L}{D}$
$\theta=\dfrac{44}{195\times 10^3}$
$\theta=2,3\times 10^{-4}\ rad$
Q2- Indiquer si l’observateur parvient à discerner la pale de l’éolienne à l’œil nu.
Le pouvoir séparateur de l’œil de l’observateur : $\varepsilon = 3,0\times 10^{-4}\ rad$
$\theta<\varepsilon$ : l’observateur ne parvient pas à discerner la pale de l’éolienne à l’œil nu.
Recours à une lunette afocale
Pour mieux discerner des objets distants, une des méthodes les plus simples est d’utiliser une lunette de visée, ou lunette afocale. Une telle lunette modifie le trajet des rayons issus des points A et B de sorte qu’ils parviennent à l’œil de l’observateur sous un nouvel angle
𝜃′ plus grand que l’angle 𝜃 initial. On appelle « grossissement » de la lunette, noté 𝐺, le rapport entre 𝜃′ et 𝜃 :
$$G=\frac{\theta’}{\theta}$$
Le critère pour pouvoir distinguer les détails d’un objet éloigné au travers de la lunette afocale devient alors :
𝜃′ > 𝜀
L’observateur souhaite fabriquer une lunette afocale pour pouvoir discerner les pales de l’éolienne. Pour cela, il a besoin de connaître la relation qui lie le grossissement de la lunette aux grandeurs caractéristiques des éléments qui la constituent.
Il choisit de réaliser la lunette en utilisant deux lentilles convergentes L1 et L2 fixées à l’extrémité de tubes pouvant coulisser l’un dans l’autre (voir document 2). La lentille L1 est orientée vers l’objet distant que l’on veut observer et l’œil est positionné après la lentille L2.
Document 2 – Schéma de la lunette astronomique artisanale (les graduations sont en centimètres)
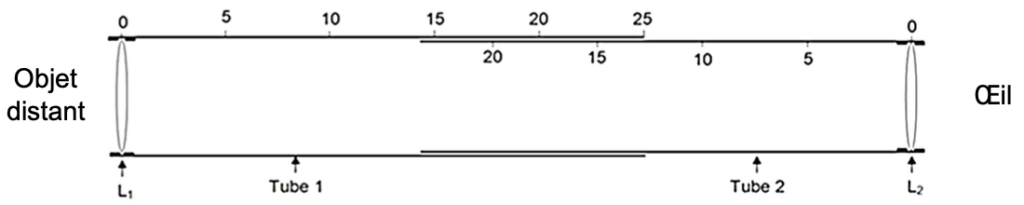
Dans la suite, on étudie ce dispositif afin d’identifier comment positionner les lentilles pour assembler une lunette afocale, puis de caractériser le grossissement de la lunette obtenue.
Pour mener cette étude, on s’appuie sur le schéma de l’ANNEXE À RENDRE AVEC LA COPIE. Il s’agit d’un schéma de principe ; il n’est pas à l’échelle.
On note :
- F1, F1′ , F2 et F2′ respectivement les foyers objets et images des lentilles L1 et L2.
- 𝑓1′ et 𝑓2′ les distances focales de ces lentilles.
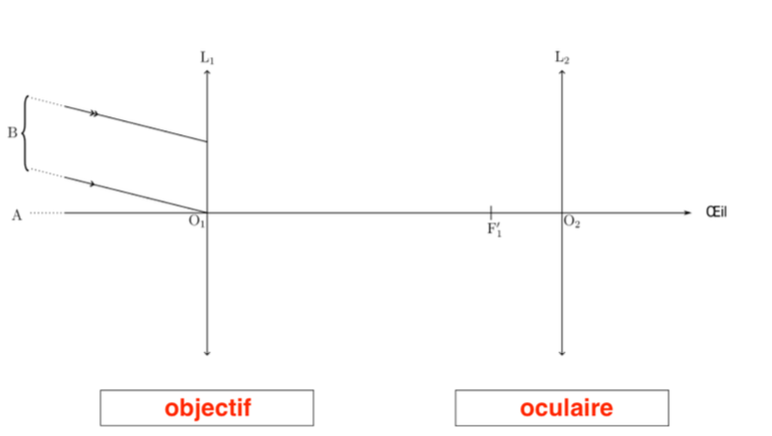
Q3- Sur le schéma de l’ANNEXE À RENDRE AVEC LA COPIE, associer aux lentilles les termes d’objectif et d’oculaire.
L1 : l’objectif car c’est une lentille convergente possédant une grande distance focale. C’est la lentille placée vers l’objet
L2 : l’oculaire car c’est une lentille convergente possédant une petite distance focale. C’est la lentille où on place l’œil.
Le principe d’une lunette afocale est de former l’image à l’infini d’un objet situé à l’infini.
Q4- En expliquant le raisonnement suivi, indiquer comment doit être positionné le foyer objet de l’oculaire par rapport au foyer image de l’objectif pour former une lunette afocale.
Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
Pour que la lunette soit afocale, les deux foyers et doivent être confondus.
Q5- Placer sur le schéma de l’ANNEXE À RENDRE AVEC LA COPIE les foyers F2 et F2′ de la lentille L2.
Comme la lunette est afocale, on place $F_2$ sur $F_1^\prime$.
La distance ${\rm OF}_2^\prime=OF_2$.
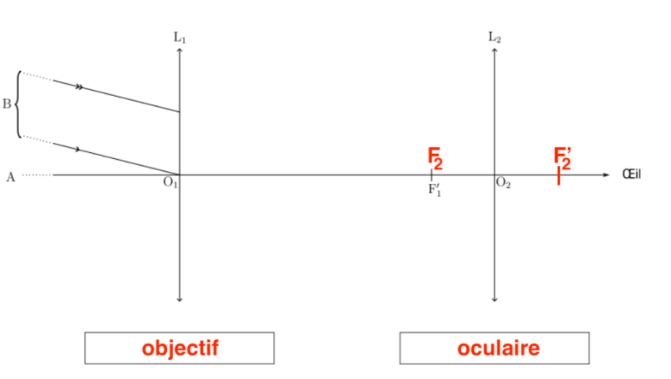
Q6- En déduire l’expression de la distance 𝑑 = O1O2 devant séparer les lentilles L1 et L2, en fonction de 𝑓1′ et 𝑓2′, pour que la lunette soit afocale.
Pour que la lunette soit afocale, les deux foyers $F_1^\prime$ et $F_2$ doivent être confondus.
Ainsi :
$O_1O_2={f^\prime}_1+{f^\prime}_2$

Pour déterminer l’expression du grossissement, on doit étudier le trajet de rayons provenant d’un point B lointain et hors axe optique.
Q7- Sur le schéma de l’ANNEXE À RENDRE AVEC LA COPIE, tracer la marche des deux rayons lumineux issus du point B lointain au travers de la lunette, en faisant apparaitre l’image intermédiaire A1B1 qui se forme dans la lunette.
Le rayon lumineux issu de B pénétrant dans la lunette par le centre optique O1 de la lentille L1 n’est pas dévié.
Position de B1 image intermédiaire de B : Comme l’objet A∞B∞ est à l’infini, son image A1B1 est dans le plan focal image de l’objectif L1.
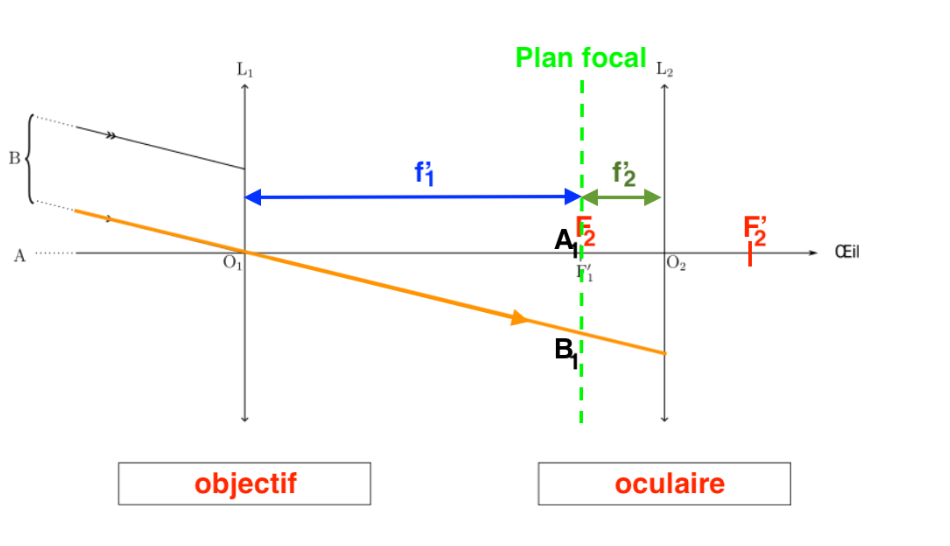
L’autre rayon lumineux issus de B, sort de L1 en passant par B1.
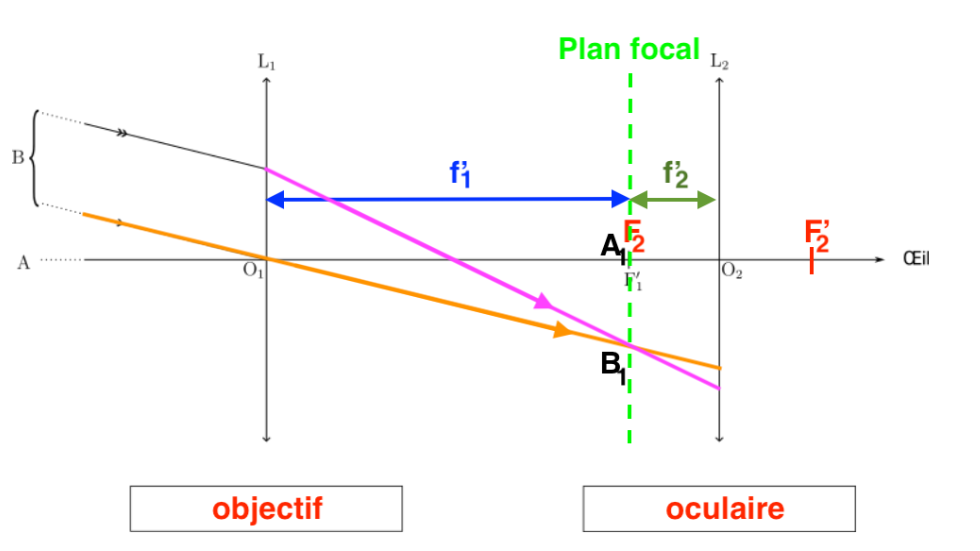
Pour le rayon émergeant de la lentille L2 :
- On trace un rayon issu de B1 passant par O2. Ce rayon ne sera pas dévié.
- De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi les rayons émergeants de la lentille L2 issue de B1 seront parallèles à ce rayon tracé.
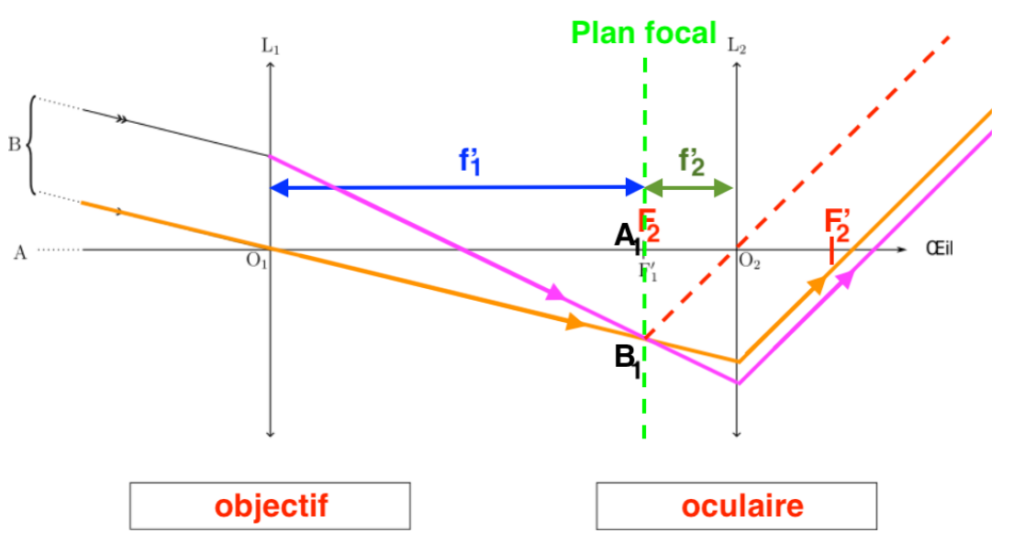
Q8- Sur le schéma de l’ANNEXE À RENDRE AVEC LA COPIE, positionner les angles 𝜃 et 𝜃′.
L’angle 𝜃 est l’angle sous lequel est vu l’objet sans la lunette.
L’angle 𝜃’ est l’angle sous lequel est vu l’objet avec la lunette.
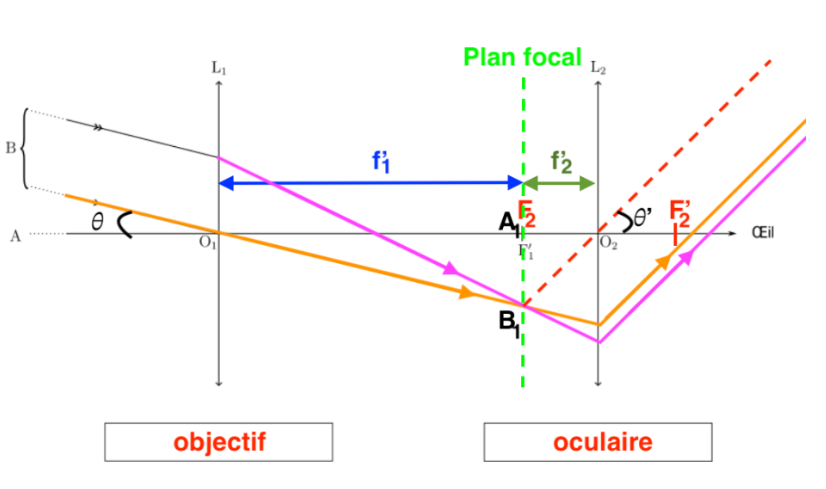
Q9- En exploitant le schéma obtenu, montrer que le grossissement 𝐺 peut être exprimé en fonction des distances focales des lentilles par la relation :
$$G=\frac{f_1′}{f_2′}$$
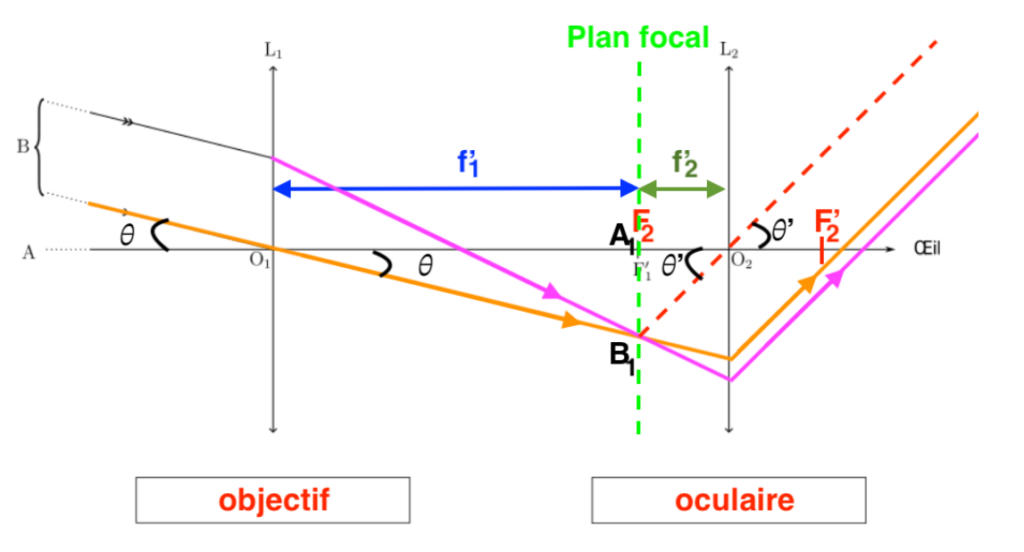
$\tan\left(\theta\right)\approx\theta=\dfrac{A_1B_1}{f_1^\prime}$
$\tan\left(\theta^\prime\right)\approx\theta^\prime=\dfrac{A_1B_1}{f_2^\prime}$
$G=\dfrac{\theta^\prime}{\theta}=\dfrac{\dfrac{A_1B_1}{f_2^\prime}}{\dfrac{A_1B_1}{f_1^\prime}}=\dfrac{A_1B_1}{f_2^\prime}\times\dfrac{f_1^\prime}{A_1B_1}=\dfrac{f_1^\prime}{f_2^\prime}$
Pour assembler la lunette, l’observateur dispose d’un ensemble de lentilles dont les distances focales sont listées ci-dessous.
Données :
- Distances focales des lentilles disponibles :
5,0 cm ; 10,0 cm ; 12,5 cm ; 20,0 cm ; 30,0 cm.
- Distance entre le lieu d’observation et la crête de l’Arcaja : 𝐷 = 195 km
- Longueur d’une pale d’éolienne : 𝐿 = 44 m
- Pouvoir séparateur de l’œil de l’observateur : 𝜀 = 3,0 × 10−4 rad
Important – critère d’observation :
On fixe comme critère que l’observateur pourra distinguer les pales « confortablement » si l’angle 𝜃′ est au moins quatre fois plus grand que le pouvoir séparateur de l’œil nu.
Q10- Proposer un choix de lentilles pour l’objectif et l’oculaire permettant à l’observateur de distinguer confortablement les pales de l’éolienne.
Pour répondre à cette question, le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.
$G=\dfrac{f_1^\prime}{f_2^\prime}$
$\dfrac{f_1^\prime}{f_2^\prime}=G$
Or
$G=\dfrac{\theta^\prime}{\theta}$
Ainsi
$\dfrac{f_1^\prime}{f_2^\prime}=\dfrac{\theta^\prime}{\theta}$
Critère que l’observateur pourra distinguer les pales « confortablement » si l’angle 𝜃′ est au moins quatre fois plus grand que le pouvoir séparateur de l’œil nu.
$\theta^\prime=4\times\varepsilon$
Ainsi
$\dfrac{f_1^\prime}{f_2^\prime}=\dfrac{4\times\varepsilon}{\theta}$
$\dfrac{f_1^\prime}{f_2^\prime}=\dfrac{4\times 3,0\times 10^{-4}}{2,3\times 10^{-4}}$
$\dfrac{f_1^\prime}{f_2^\prime}=5,2$
$f_1^\prime=5,2\times f_2^\prime$
Au minimum $f_1^\prime$ doit être 5,2 fois plus grand que $f_2^\prime$
Si on prend la plus petite valeur $f_2^\prime=5,0\ cm$ : $f_1^\prime=5,2\times f_2^\prime=5,2\times 5,0=26\ cm$
Il faut choisir une lentille de distance focale supérieure à 26 cm :
Ainsi, on choisit $f_2^\prime=5,0\ cm$ et $f_1^\prime=30\ cm$

ANNEXE À RENDRE AVEC LA COPIE
Exercice 2 – Schéma de la lunette afocale
Indiquer la fonction de chaque lentille (objectif ou oculaire) dans les cadres sous les lentilles.