Liban 2022 Sujet 1
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1LR1
Sujet et corrigé
Mots-clés : deuxième loi de Newton ; période de révolution ; lunette astronomique.
Les 18 mars et 22 avril 2020, deux fusées ont chacune mis en orbite soixante satellites de type « Starlink ». À terme, ce sont près de 12 000 satellites similaires qui doivent être mis en orbite.
L’objectif est de constituer un réseau de satellites, permettant un accès à internet en tout point de la planète.
Données :
- masse de la Terre : MT = 5,97×1024 kg ;
- rayon de la Terre : RT = 6 400 km ;
- constante de gravitation universelle : G = 6,67×10-11 m3⋅kg-1⋅s-2 ;
- l’étude est conduite dans le référentiel géocentrique : son origine coïncide avec le centre O de la Terre et ses axes pointent vers des étoiles lointaines. Il est supposé galiléen.
Données techniques d’un satellite Starlink :
- masse : 227 à 260 kg ;
- altitude h : entre 340 et 1 200 km ;
- vitesse de déplacement sur son orbite dans le référentiel géocentrique : vS = 2,73×104 km⋅h-1 ;
- taille : environ 1,0 m × 1,0 m × 1,0 m.
Orbite d’un satellite Starlink
Le mouvement d’un satellite Starlink est circulaire.
Le schéma ci-contre, qui n’est pas à l’échelle, représente une partie de la trajectoire du satellite S.
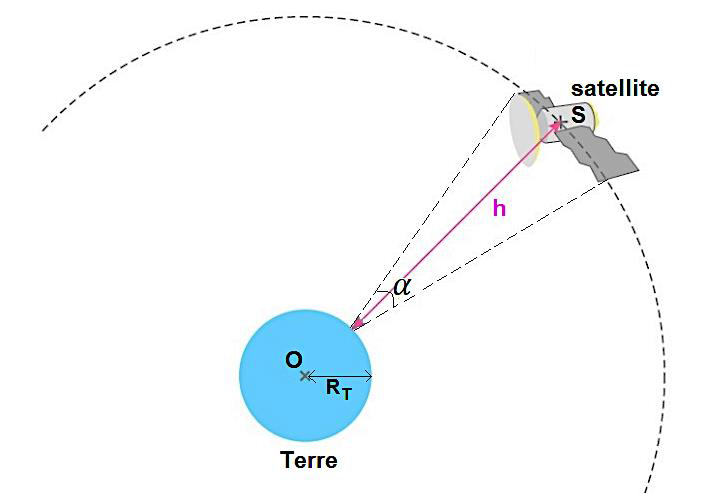
L’altitude du satellite est notée h et son diamètre apparent depuis la surface de la Terre est l’angle noté α défini sur le schéma ci-contre.
1. Justifier à l’aide de la deuxième loi de Newton que le mouvement du satellite est uniforme.
Réponse :
Système : Starlink
Référentiel : Géocentrique supposé galiléen
D’après la 2nd loi de Newton :
$\sum_{}^{}\overrightarrow{F_{ext}}=M_{S}\overrightarrow{a}$
$\overrightarrow{F}_{T/S}=M_{S}\overrightarrow{a}$
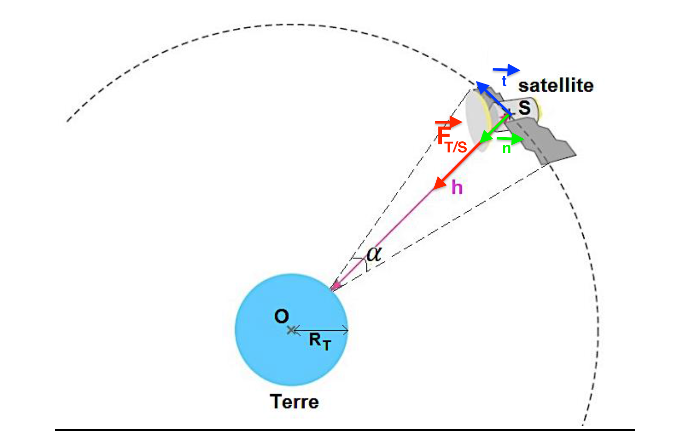
$G\times \frac{M_{S}\times M_{T}}{(R_{T}+h)^2}\overrightarrow{n}=M_{S}\overrightarrow{a}$
$\overrightarrow{a}_{S}=G\times \frac{M_{T}}{r^2}\overrightarrow{n}$
Or, pour un mouvement circulaire, dans la base de Frenet, le vecteur accélération est de la forme :
$\vec{a}_{S}=\frac{v_{S}^2}{r}\vec{n}+\frac{dv_{S}}{dt}\vec{t}$
L’accélération étant unique, par identification :
$\frac{dv_{S}}{dt}=0$ donc la vitesse est constante : le mouvement du satellite est uniforme.
2. Définir puis exprimer la période de révolution T en fonction de la vitesse vS du satellite, du rayon terrestre RT et de l’altitude h du satellite.
Réponse :
La période de révolution est :
$T=\frac{\text{préimetre d’un cercle}}{vitesse}=\frac{2\pi\left( R_T+h \right)}{v_S}$
3. À l’aide de la deuxième loi de Newton, exprimer RT + h en fonction de G, MT et vS.
Réponse :
$\overrightarrow{a}_{S}=G\times \frac{M_{T}}{\left( R_T+h \right)^2}\overrightarrow{n}$
Or, pour un mouvement circulaire, dans la base de Frenet, le vecteur accélération est de la forme :
$\vec{a}_{S}=\frac{v_{S}^2}{\left( R_T+h \right)}\vec{n}+\frac{dv_{S}}{dt}\vec{t}$
L’accélération étant unique, par identification :
$\frac{v_{S}^2}{\left( R_T+h \right)}=G\ \times \frac{M_T}{\left( R_T+h \right)^2}$
$v_{S}^{2}=G \times \frac{M_T}{\left( R_T+h \right)^2}\times\left( R_T+h \right)$
$v_{S}^{2}=G \times \frac{M_T}{\left( R_T+h \right)}$
$R_T+h=G \times \frac{M_T}{v_{S}^{2}}$
4. Calculer l’altitude h du satellite. Commenter.
Réponse :
$$R_T + h = G \times \frac{M_T}{v_S^2}$$
$$h = G \times \frac{M_T}{v_S^2} – R_T$$
$$h = 6,67 \times 10^{-11} \times \frac{5,97 \times 10^{24}}{\left(\frac{2,73 \times 10^4}{3,6}\right)^2} – 6400 \times 10^3$$
$$h = 5,24 \times 10^5\ \text{m}$$
$$h = 524\ \text{km}$$
C’est cohérent avec les données « altitude h : entre 340 et 1 200 km »
Observation du satellite
Le satellite peut être observé grâce à une lunette astronomique, instrument d’optique afocal constitué d’un objectif et d’un oculaire.
L’objectif (L1) de la lunette utilisée est modélisé par une lentille mince de distance focale f1‘ = 600 mm et l’oculaire (L2) par une lentille mince de distance focale f2‘ = 32 mm.
5. Donner la signification du terme afocal.
Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
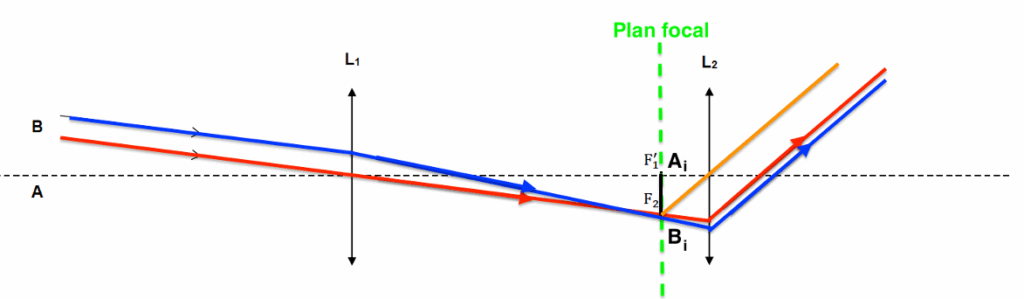
6. Le satellite est schématisé comme un objet AB perpendiculaire à l’axe optique, situé très loin de l’objectif (à « l’infini »). Sur l’annexe à rendre avec la copie, construire l’image intermédiaire, AiBi, de AB, donnée par l’objectif, puis construire l’image finale, AfBf de l’objet AB par la lunette astronomique.
Le rayon lumineux issu de $B$ pénétrant dans la lunette par le centre optique $O_1$ de la lentille $L_1$ n’est pas dévié.

Position de $B_i$ (image intermédiaire de $B$) :
Comme $B$ est à l’infini, son image $B_i$ est dans le plan focal image de l’objectif $L_1$.
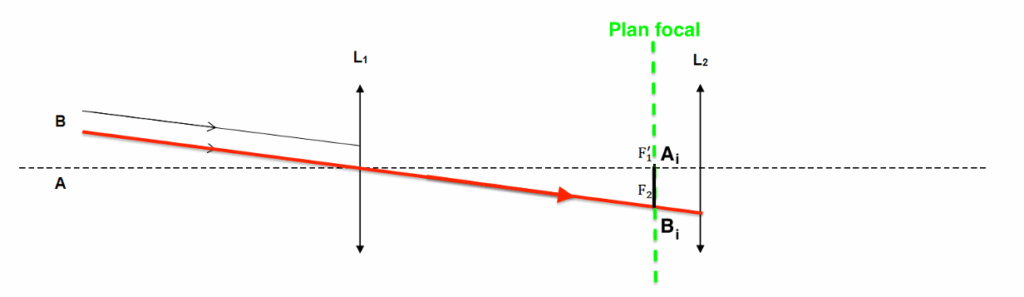
L’autre rayon lumineux issu de $B$ est dévié vers $B_i$.
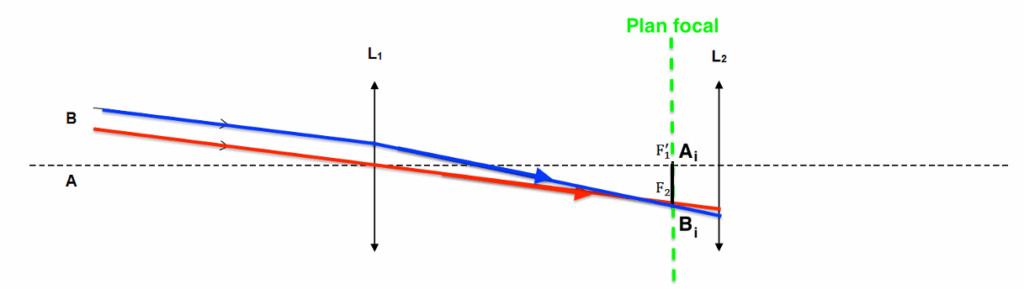
Pour les rayons émergeants de la lentille L2 :
- On trace un rayon issu de $B_i$ passant par O2. Ce rayon ne sera pas dévié.
- De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi les rayons émergeants de la lentille L2 issue de seront parallèles à ce rayon tracé.
7. Avec l’aide du schéma ci-dessous, exprimer le diamètre apparent 𝛼 correspondant à l’angle sous lequel les deux extrémités A et B du satellite sont observées depuis la surface de la Terre dans les conditions les plus favorables.
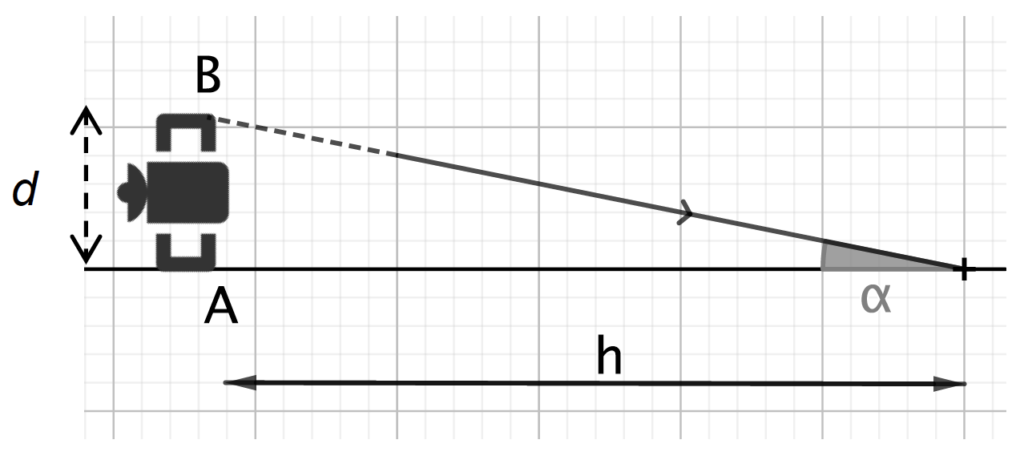
$$\tan(\alpha) \approx \alpha = \frac{d}{h}$$
Notre œil n’est pas capable de distinguer les détails d’un objet dont le diamètre apparent est inférieur à αmin = 2,9 ×10-4 rad.
8. Indiquer si les points A et B d’un satellite Starlink peuvent être distingués à l’œil nu. On suppose que h = 520 km.
$$\alpha = \frac{d}{h}$$
$$\alpha = \frac{1,0}{520 \times 10^3}$$
$$\alpha = 1,9 \times 10^{-6}\ \text{rad}$$
$$\alpha_{min} = 2,9 \times 10^{-4}\ \text{rad}$$
$\alpha < \alpha_{min}$
Ainsi, le satellite ne peut pas être distingué à l’œil nu.
Le grossissement GL de la lunette a pour expression :
$G_L=\frac{\alpha’}{\alpha}=\frac{f_1′}{f_2′}$
où l’angle α’ représente le diamètre apparent de l’image du satellite à travers la lunette astronomique.
9. Montrer que la lunette utilisée dans cet exercice ne permet pas d’observer les détails d’un satellite Starlink.
$$G = \frac{\alpha’}{\alpha} = \frac{f_1′}{f_2′}$$
$$\alpha’ = \frac{f_1′}{f_2′} \times \alpha$$
$$\alpha’ = \frac{600 \times 10^{-3}}{32 \times 10^{-3}} \times 1,9 \times 10^{-6}$$
$$\alpha’ = 3,6 \times 10^{-5}\ \text{rad}$$
$\alpha’ < \alpha_{min}$
La lunette utilisée dans cet exercice ne permet donc pas d’observer les détails d’un satellite Starlink.
ANNEXE À RENDRE AVEC LA COPIE

