Bac Métropole Septembre 2023 Sujet 1
Exercice 1 – (11 points) – Durée 1h56 – Calculatrice autorisée
Sujet n°23-PYCJ1ME3
Sujet et corrigé
EXERCICE 1 – OBSERVATION ORNITHOLOGIQUE D’UNE OIE CENDRÉE (11 points)
Certains parcs ornithologiques proposent des sorties mêlant observations des oiseaux, suivies d’analyse d’échantillons récoltés comme par exemple des plumes.
Cet exercice s’intéresse dans un premier temps à l’observation d’une oie cendrée à l’œil nu et à l’aide d’une longue-vue. Puis, dans un second temps, le phénomène d’interférences lumineuses est utilisé pour déterminer des dimensions caractéristiques de la structure d’une plume d’oie.

Oie cendrée
Données :
- taille approximative d’une oie cendrée : 80 cm ;
- taille approximative du bec d’une oie cendrée : 7 cm ;
- distance focale de l’objectif L1 de la longue-vue : f1′ = 450 mm ;
- distance focale de l’oculaire L2 de la longue-vue : f2′ = 30 mm ;
- relation de conjugaison pour une lentille L de centre optique O : $\frac{1}{\overline{OA’}}-\frac{1}{\overline{OA}}=\frac{1}{f’}$ où $\overline{OA’}$ est la distance algébrique entre le centre optique de la lentille L et le point A’, $\overline{OA}$ est la distance algébrique entre le centre optique de la lentille L et le point A et f ’ est la distance focale de la lentille ;
- grandissement transversal $\gamma=\frac{\overline{OA’}}{\overline{OA}}=\frac{\overline{A’B’}}{\overline{AB}}$ où $\overline{A’B’}$ est la taille algébrique de l’image A’B’ et $\overline{AB}$ est celle de l’objet AB ;
- approximation dans le cas de petits angles (θ << 1 rad) : sin θ = θ ; tan θ= θ.
1. Observation d’une oie cendrée à l’œil nu
L’œil est un système complexe que l’on peut modéliser par l’association :
d’un écran situé à une distance D = 17 mm du centre optique O.
d’une lentille mince convergente L, d’axe optique Δ, de distance focale $f’=\overline{OF’}=17\ \text{mm}$, de centre optique O ;
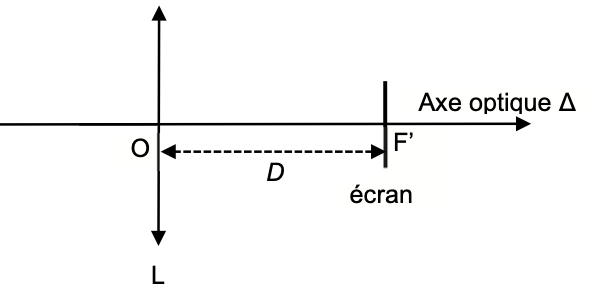
Figure 1. Schéma simplifié du modèle de l’œil
La rétine est une membrane qui tapisse le fond de l’œil et qui joue le rôle d’écran. L’oie cendrée est modélisée par un objet de hauteur AB perpendiculaire à l’axe optique en A et situé à 280 m du centre optique O. L’image de AB à travers la lentille L est notée A’B’.
Q1. Justifier que la position de l’image A’B’ de l’oie par la lentille L est telle que $\overline{OA’}$ = 17 mm.
Utilisons la relation de conjugaison pour trouver $\overline{OA\prime}$ :
$$\frac{1}{\overline{OA\prime}}-\frac{1}{\overline{OA}}=\frac{1}{f\prime}$$
$$\frac{1}{\overline{OA\prime}}=\frac{1}{f\prime}+\frac{1}{\overline{OA}}$$
$$\frac{1}{\overline{OA\prime}}=\frac{1\times\overline{OA}}{f\prime\times\overline{OA}}+\frac{1\times f\prime}{\overline{OA}\times f\prime}$$
$$\frac{1}{\overline{OA\prime}}=\frac{\overline{OA}+f\prime}{f\prime\times\overline{OA}}$$
$$\overline{OA\prime}=\frac{f\prime\times\overline{OA}}{\overline{OA}+f\prime}$$
$$\overline{OA\prime}=\frac{17\times10^{-3}\times-280}{-280+17\times10^{-3}}$$
$$\overline{OA\prime}=1,7\times10^{-2}\ \text{m}$$
$$\overline{OA\prime}=17\times10^{-3}\ \text{m}$$
$$\overline{OA\prime}=17\ \text{mm}$$
Q2. Vérifier que la taille de l’image A’B’ de l’oie sur la rétine de l’observateur est voisine de 49 µm. Sachant que la rétine est assimilée à un disque de rayon égal à 6 mm centré en F’, préciser si l’oie est vue en entier par un observateur.
Utilisons la relation de grandissement transversal pour trouver $\overline{A\prime B\prime}$ :
$$\gamma=\frac{\overline{OA\prime}}{\overline{OA}}=\frac{\overline{A\prime B\prime}}{\overline{AB}}$$
$$\frac{\overline{A\prime B\prime}}{\overline{AB}}=\frac{\overline{OA\prime}}{\overline{OA}}$$
$$\overline{A\prime B\prime}=\frac{\overline{OA\prime}}{\overline{OA}}\times\overline{AB}$$
$$\overline{A\prime B\prime}=-4,9\times10^{-5}\ \text{m}$$
$$\overline{A\prime B\prime}=-49\times10^{-6}\ \text{m}$$
$$\overline{A\prime B\prime}=-49\ \mu\text{m}$$
Le signe – nous indique que l’image est renversée.
Ainsi, la taille de l’image A’B’ de l’oie sur la rétine de l’observateur est voisine de 49 μm.
Comparons la taille de l’image A’B’ et la taille de la rétine :
$49\ \mu\text{m}=49\times10^{-6}\ \text{m}=4,9\times10^{-5}\ \text{m}<6\times10^{-3}\ \text{m}$
$A\prime B\prime<\text{taille de la rétine}$
Ainsi, l’oie est vue en entier par un observateur.
Le pouvoir séparateur de l’œil humain est l’angle limite, noté αm, sous lequel un objet peut être vu distinctement par l’œil (voir figure 2) ; sa valeur est de 3×10–4 rad.
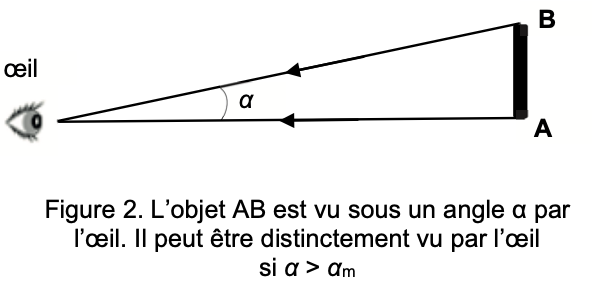
Figure 2. L’objet AB est vu sous un angle α par l’œil. Il peut être distinctement vu par l’œil si α > αm
Q3. Déterminer la distance minimale séparant deux points A et B d’un objet pouvant être vus lorsqu’ils sont situés à une distance de 280 m de l’œil. En déduire si l’oie peut être vue distinctement par l’observateur à l’œil nu puis déterminer si le bec de l’oie peut être observé distinctement.
$$\tan\alpha=\frac{\text{Opposé}}{\text{Adjacent}}$$
$$\tan\alpha=\frac{AB}{d}$$
$$AB=d\times\tan\alpha$$
Or dans le cas de petits angles :
$$\tan\alpha=\alpha$$
Ainsi
$$AB=d\times\alpha$$
$$AB=280\times3\times10^{-4}$$
$$AB=8\times10^{-2}\ \text{m}$$
$$AB=8\ \text{cm}$$
La distance minimale séparant deux points A et B d’un objet pouvant être vus lorsqu’ils sont situés à une distance de 280 m de l’œil est $AB=8\ \text{cm}$.
La taille approximative d’une oie cendrée est 80 cm qui est supérieure à la taille minimale.
Ainsi, l’oie peut être vue distinctement par l’observateur à l’œil nu.
La taille approximative du bec d’une oie cendrée est 7 cm qui est inférieure à la taille minimale.
Ainsi, le bec de l’oie ne peut pas être observé distinctement à l’œil nu.
2. Observation avec une longue-vue assimilée à une lunette astronomique afocale
L’oie est désormais observée à l’aide d’une longue-vue assimilée à une lunette astronomique afocale. Cette lunette est composée d’une lentille L1 de distance focale f1 ’ jouant le rôle de l’objectif et d’une lentille L2 de distance focale f2’ jouant le rôle de l’oculaire. On considère que l’oie, modélisée par un objet AB perpendiculaire à l’axe optique en A, est « à l’infini ». L’image de AB à travers la lentille L1 est notée A1 B1 . L’image de A1 B1 à travers la lentille L2 est notée A2B2.
Q4. Compléter la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE pour représenter l’image A1 B1 formée par la lentille L1 d’un objet AB (représentant l’oie) situé à l’infini.
La lentille L1, donne de l’objet $A_\infty B_\infty$, une image $A_1B_1$ sur le plan focal.
Le rayon issu de B, passant par O1 n’est pas dévié.
Le point B1 est défini par l’intersection de ce rayon et le plan focal.
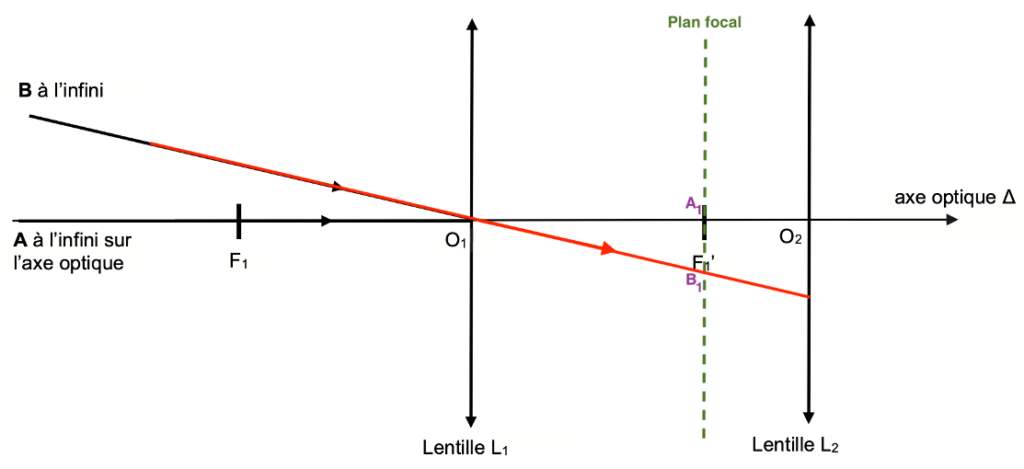
Q5. Placer, en justifiant, le foyer objet F2 de la lentille L2 sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE.
Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
Pour que la lentille L2, donne de l’objet $A_1B_1$, une image à l’infini, il faut que celui-ci soit sur le foyer $F_2$.
Ainsi, les deux foyers $F_1^\prime$ et $F_2$ sont confondus.
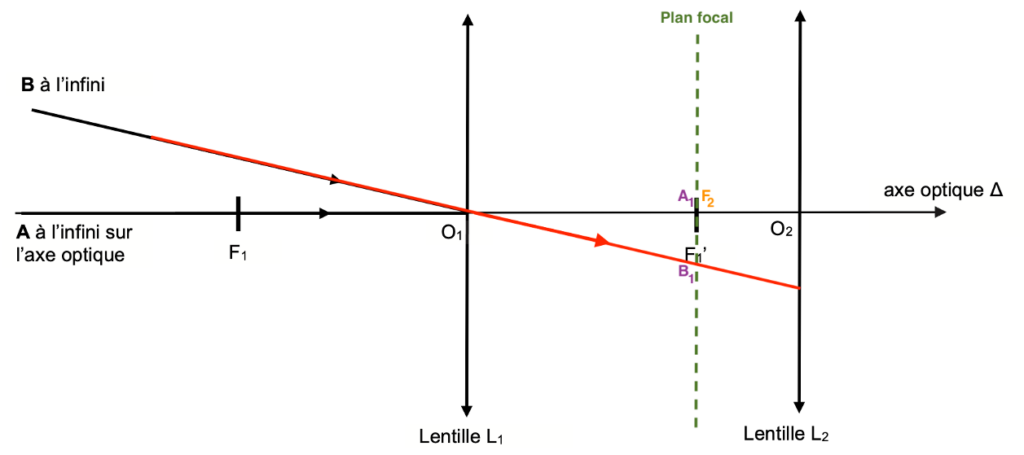
Une lunette astronomique est caractérisée par son grossissement d’expression :
$$G=\frac{\alpha’}{\alpha}$$
avec α l’angle sous lequel l’objet AB est vu à l’œil nu et α’ l’angle sous lequel l’image A2B2 est vue à travers la lunette astronomique afocale.
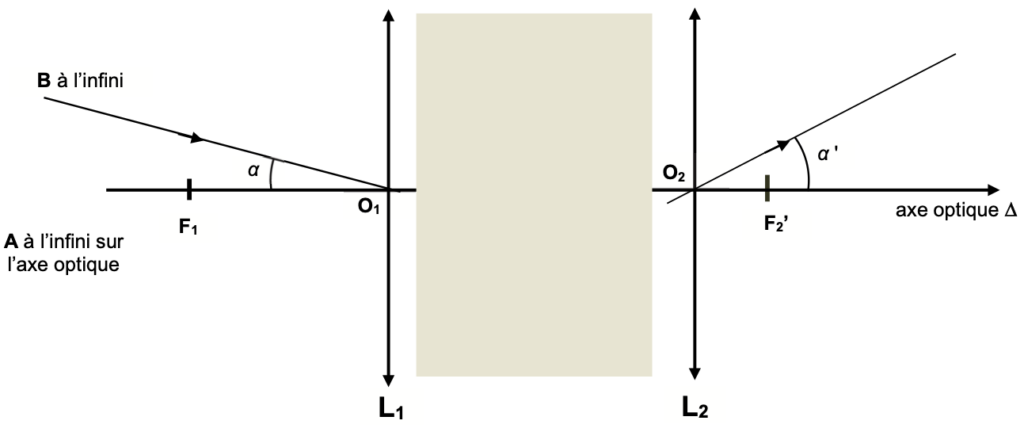
Figure 3. Représentation, sans souci d’échelle, de la lunette astronomique.
Q6. En considérant les angles α et α’ exprimés en radians comme petits, montrer que le grossissement de la lunette astronomique afocale peut s’exprimer par la relation :
$$G=\frac{f_1′}{f_2′}$$
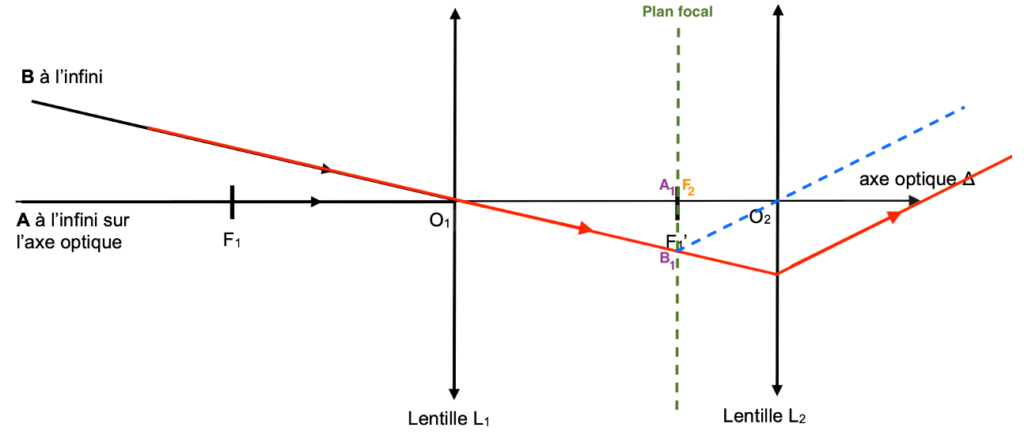
Un rayon issu de B1 passant par O2 n’est pas dévié.
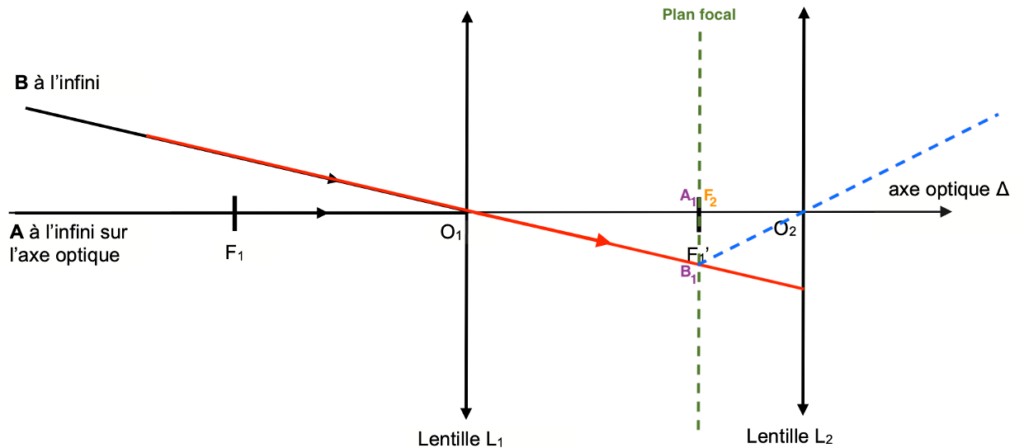
$A_1B_1$ étant sur le plan focal, il donnera une image à l’infini, tous les rayons issus de B1, passant par la lentille L2 seront parallèles.
Plaçons $\alpha$ et $\alpha^\prime$ :
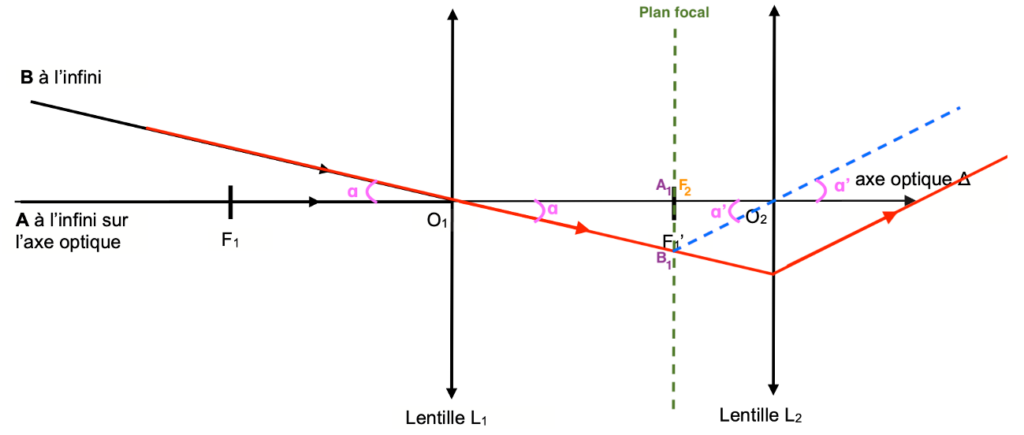
Le grossissement $G$ est défini par :
$$G=\frac{\alpha^\prime}{\alpha}$$
$$\tan(\alpha)\approx\alpha=\frac{A_1B_1}{f_1^\prime}$$
$$\tan(\alpha^\prime)\approx\alpha^\prime=\frac{A_1B_1}{f_2^\prime}$$
$$G=\frac{\alpha^\prime}{\alpha}=\frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}}=\frac{A_1B_1}{f_2^\prime}\times\frac{f_1^\prime}{A_1B_1}=\frac{f_1^\prime}{f_2^\prime}$$
On peut s’appuyer sur la figure A1 de l’ANNEXE À RENDRE AVEC LA COPIE.
Q7. Calculer la valeur du grossissement G de la lunette astronomique afocale.
$$G=\frac{f_1^\prime}{f_2^\prime}$$
$$G=\frac{450\times10^{-3}}{30\times10^{-3}}$$
$$G=15$$
Q8. Indiquer en justifiant si l’observateur voit distinctement, à travers la longue-vue, le bec de l’oie située à 280 m.
Calculons l’angle sous lequel est vu le bec de l’oie à l’œil nu :
$$\tan\alpha=\frac{AB}{d}$$
Or dans le cas de petits angles :
$$\tan\alpha=\alpha$$
$$\alpha=\frac{AB}{d}$$
$$\alpha=\frac{7\times10^{-2}}{280}$$
$$\alpha=2,5\times10^{-4}\ \text{rad}$$
Calculons l’angle sous lequel est vu le bec de l’oie à travers la longue-vue :
$$G=\frac{\alpha^\prime}{\alpha}$$
$$\alpha^\prime=G\times\alpha$$
$$\alpha^\prime=15\times2,5\times10^{-4}$$
$$\alpha^\prime=3,8\times10^{-3}\ \text{rad}$$
D’après le sujet : le pouvoir séparateur de l’œil humain est l’angle limite, noté $\alpha_m$, sous lequel un objet peut être vu distinctement par l’œil ; sa valeur est de $3\times10^{-4}\ \text{rad}$.
$$\alpha^\prime>\alpha_m$$
Ainsi, l’observateur voit distinctement, à travers la longue-vue, le bec de l’oie située à 280 m.
3. Structure de la plume d’oie cendrée
Pour identifier l’espèce d’un oiseau, la plume est une des parties du corps de l’animal qu’il est possible d’étudier. Les plumes d’oiseaux sont des objets complexes qui possèdent des structures géométriques périodiques à des échelles différentes, qu’il est possible d’étudier par des méthodes interférométriques.
L’expérience des fentes d’Young permet d’obtenir sur un écran une figure d’interférences constituée d’une succession de franges brillantes et sombres qui se répartissent sur un axe de direction parallèle à la droite joignant les deux fentes.

Plume d’oie
La figure 4 donne une schématisation d’une expérience des fentes d’Young, de centres F1 et F2, ainsi qu’une photographie de la figure d’interférences obtenue.
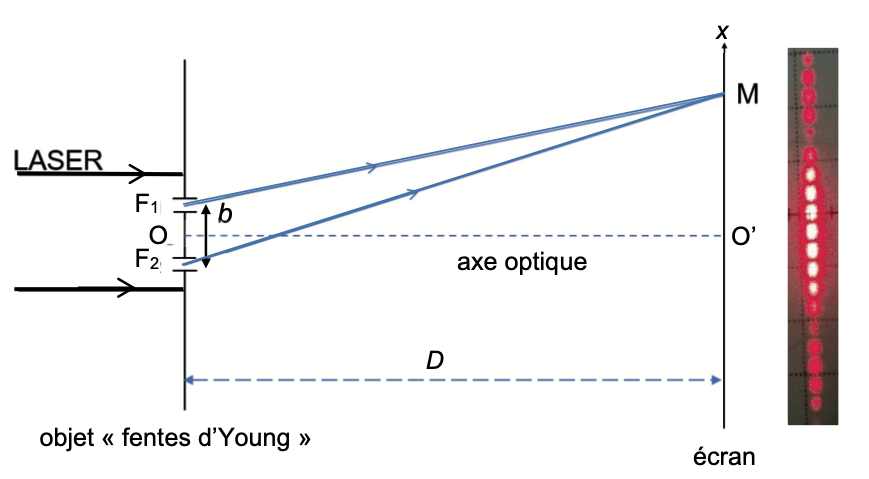
Figure 4. Schéma du dispositif expérimental.
Un faisceau lumineux issu d’un laser de longueur d’onde λ, éclaire un objet plan totalement opaque en dehors de deux fentes, séparées d’une distance notée b. Cet objet est appelé objet « fentes d’Young ».
Le faisceau est constitué d’un ensemble de rayons parallèles, et se propage parallèlement à l’axe optique (OO’), le point O étant à égale distance des points F1 et F2 et le point O’ étant situé sur l’écran.
Les ondes issues des fentes interfèrent sur l’écran. En un point M de celui-ci, on admet que la différence de chemin optique entre les deux ondes s’écrit δ = F2M – F1M (voir figure 4).
L’écran est situé à une distance D des fentes très grande devant la distance b (D >> b).
Q9. Préciser la condition que doit vérifier la différence de chemin optique δ pour que les ondes issues des fentes interfèrent de manière constructive au point M. Indiquer en justifiant dans ce cas si la frange au point O’ est brillante ou sombre.
Pour que les ondes issues des fentes interfèrent de manière constructive au point M, la différence de chemin optique $\delta$ doit vérifier la condition :
$$\delta=k\times\lambda$$
Au point O’ :
$$\delta=F_2O^\prime-F_1O^\prime$$
Or $F_2O^\prime=F_1O^\prime$
Donc $\delta=0\ \text{m}$
Ainsi, au point O’, $\delta=k\times\lambda$ avec $k=0$ : les ondes issues des fentes interfèrent de manière constructive au point O’, la frange au point O’ est brillante.
Sur la figure 5, le point H représente le projeté orthogonal de F1 sur le segment [F2M]. On admet que la différence de chemin optique δ est égale à la longueur du segment [F2H].
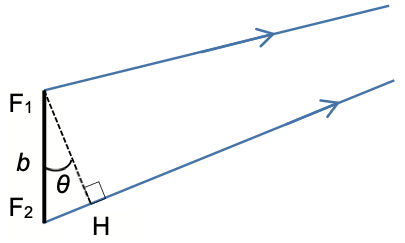
Figure 5. Agrandissement du schéma au niveau des fentes d’Young
Q10. Montrer que, dans les conditions de l’expérience (θ << 1 rad), il est possible d’exprimer la différence de chemin optique par la relation suivante :
δ = b · θ
D’après le sujet : on admet que la différence de chemin optique $\delta$ est égale à la longueur du segment $[F_2H]$.
$$\delta=F_2H$$
Dans le cas de petits angles $(\theta\ll1\ \text{rad})$ : $\sin\theta=\theta$
$$\sin\theta=\frac{F_2H}{b}$$
Ainsi
$$\theta=\frac{F_2H}{b}$$
$$F_2H=\theta\times b$$
Donc
$$\delta=b\times\theta$$
On montre, avec une très bonne approximation, que l’angle θ est égal à l’angle $\widehat{O’OM}$ rectangle O’OM représenté sur la figure 6. L’abscisse du point M sur l’axe O’x est notée x.
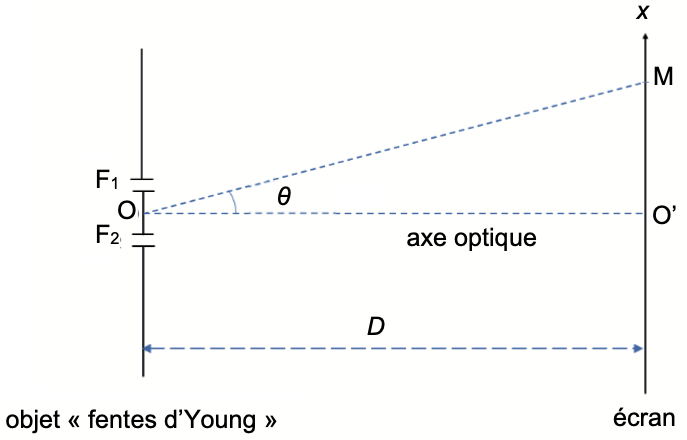
Figure 6. Mise en évidence de l’angle θ dans le triangle O’OM
Q11. Après avoir exprimé l’angle θ en fonction de D et x, montrer que la différence de chemin optique δ a pour expression :
$$\delta=\frac{b\cdot x}{D}$$
Dans le cas de petits angles $(\theta\ll1\ \text{rad})$ : $\tan\theta=\theta$
$$\tan\theta=\frac{x}{D}$$
Donc
$$\theta=\frac{x}{D}$$
Or $\delta=b\times\theta$
Donc
$$\delta=b\times\frac{x}{D}$$
$$\delta=\frac{b\times x}{D}$$
Q12. En déduire l’expression des abscisses xk des franges brillantes, en fonction de λ, D, b et d’un entier relatif k.
$$\delta=\frac{b\times x}{D}$$
$$\frac{b\times x}{D}=\delta$$
$$b\times x=\delta\times D$$
$$x=\frac{\delta\times D}{b}$$
Or pour que les ondes issues des fentes interfèrent de manière constructive au point M, la différence de chemin optique $\delta$ doit vérifier la condition :
$$\delta=k\times\lambda$$
Ainsi
$$x_k=\frac{k\times\lambda\times D}{b}$$
Q13. Montrer que l’interfrange i est donnée par l’expression littérale suivante :
$$i=\frac{\lambda\cdot D}{b}$$
L’interfrange, notée 𝑖, est par définition la distance entre deux franges de même nature consécutives.
$$i=x\left(k+1\right)-x\left(k\right)$$
$$i=\frac{\left(k+1\right)\times\lambda\times D}{b}-\frac{k\times\lambda\times D}{b}$$
$$i=\frac{\left(k+1\right)\times\lambda\times D-k\times\lambda\times D}{b}$$
$$i=\frac{k\times\lambda\times D+1\times\lambda\times D-k\times\lambda\times D}{b}$$
$$i=\frac{1\times\lambda\times D}{b}$$
$$i=\frac{\lambda\times D}{b}$$
La figure 7 montre qu’une plume d’oie est composée d’un ensemble de barbes (tiges) fixées sur le rachis (axe principal de la plume d’oie). Les barbes supportent des éléments plus petits et fins, invisibles à l’œil nu, appelés barbules. Les barbes sont régulièrement espacées d’une distance notée bbarbe, les barbules sont également régulièrement espacées d’une distance notée bbarbule (voir figure 7) et sont dans une direction pratiquement perpendiculaire à celle des barbes. Les barbules sont plus resserrées que les barbes, on a donc bbarbule < bbarbe.
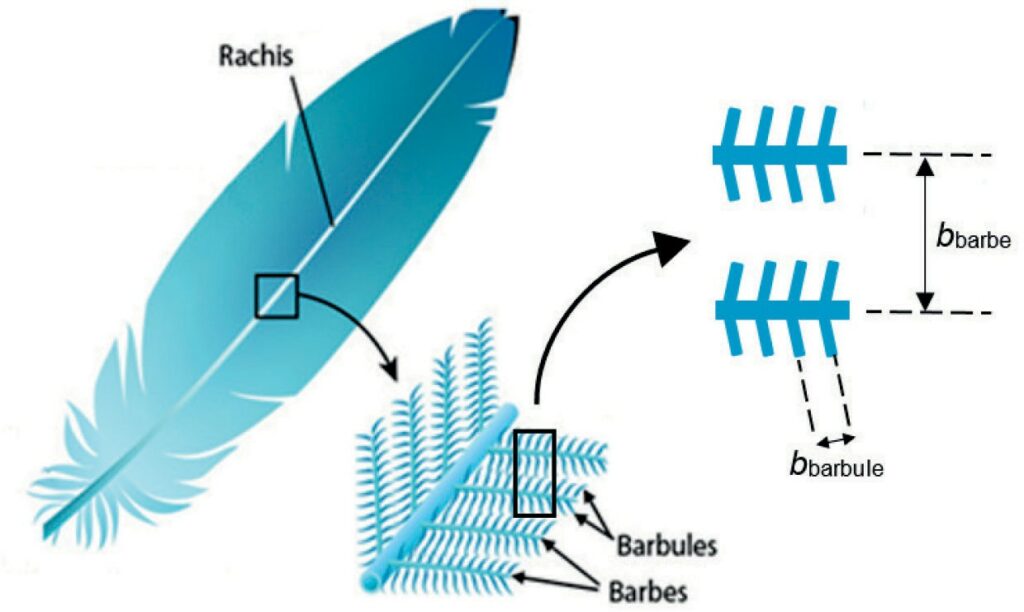
Figure 7. Schéma simplifié d’une plume (d’après https://askabiologist.asu.edu)
On réalise la même expérience que celle décrite dans la figure 4 en remplaçant l’objet « fentes d’Young » par une plume d’oie, éclairée avec un laser dont la longueur d’onde est λ = 650 nm. L’écran est placé à une distance D = 74 cm de la plume. On obtient alors une figure d’interférences dont la photographie (en négatif) est donnée sur figure A2 de l’ANNEXE À RENDRE AVEC LA COPIE.
L’écran est rapporté à un repère d’origine O’ et d’axes O’x et O’y orthogonaux.
Dans un modèle très simplifié, il est possible de montrer que les interférences sont constructives uniquement en des points de coordonnées (xk, yℓ), vérifiant les relations
$$x_k = k \cdot \frac{\lambda \cdot D}{b_{\text{barbe}}} \quad \text{et} \quad y_\ell = \ell \cdot \frac{\lambda \cdot D}{b_{\text{barbule}}}$$
où k et 𝑃 sont des entiers relatifs.
Le modèle prévoit que seulement certains de ces points sont lumineux du fait de détails de la géométrie des plumes auxquels on ne s’intéresse pas ici.
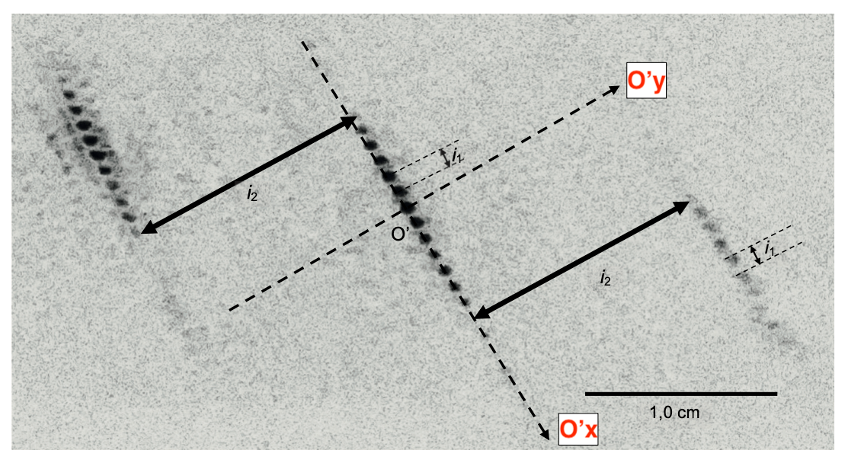
Q14. Montrer que le modèle simplifié permet d’expliquer certaines caractéristiques de la figure d’interférences observée sur la figure A2 de l’ANNEXE À RENDRE AVEC LA COPIE. Dans les cases vides de cette figure, identifier, en justifiant, l’axe O’x puis l’axe O’y.
$$i=\frac{\lambda\times D}{b}$$
$$i_{barbule}=\frac{\lambda\times D}{b_{barbule}}$$
$$i_{barbe}=\frac{\lambda\times D}{b_{barbe}}$$
$$b_{barbule}<b_{barbe}$$
$$\frac{1}{b_{barbule}}>\frac{1}{b_{barbe}}$$
$$\frac{\lambda\times D}{b_{barbule}}>\frac{\lambda\times D}{b_{barbe}}$$
$$i_{barbule}>i_{barbe}$$
$$i_2>i_1$$
La figure d’interférences observée sur la figure A2 de l’ANNEXE À RENDRE AVEC LA COPIE montre effectivement que
$$i_2>i_1.$$
Ainsi, le modèle simplifié permet d’expliquer certaines caractéristiques de la figure d’interférences observée sur la figure A2 de l’ANNEXE À RENDRE AVEC LA COPIE.
Modèle simplifié :
$$x_k=k\times\frac{\lambda\times D}{b_{barbe}}$$
$$y_l=l\times\frac{\lambda\times D}{b_{barbule}}$$
$$b_{barbule}<b_{barbe}$$
$$\frac{1}{b_{barbule}}>\frac{1}{b_{barbe}}$$
$$\frac{\lambda\times D}{b_{barbule}}>\frac{\lambda\times D}{b_{barbe}}$$
$$l\times\frac{\lambda\times D}{b_{barbule}}>k\times\frac{\lambda\times D}{b_{barbe}}$$
$$y_l>x_k$$
Q15. En exploitant la figure A2 de l’ANNEXE À RENDRE AVEC LA COPIE, évaluer les valeurs des interfranges i1 et i2 puis en déduire les valeurs des espacements bbarbule et bbarbe.
| Schéma | Réel |
| 3,9 cm | 1,0 cm |
| 5,0 cm | $i_2$ |
$$i_2=\frac{5,0\times 1,0}{3,9}$$
$$i_2=1,3\ cm$$
$$i_2=1,3\times{10}^{-2}\ m$$
| Schéma | Réel |
| 3,9 cm | 1,0 cm |
| 3,8 cm | $10\ i_1$ |
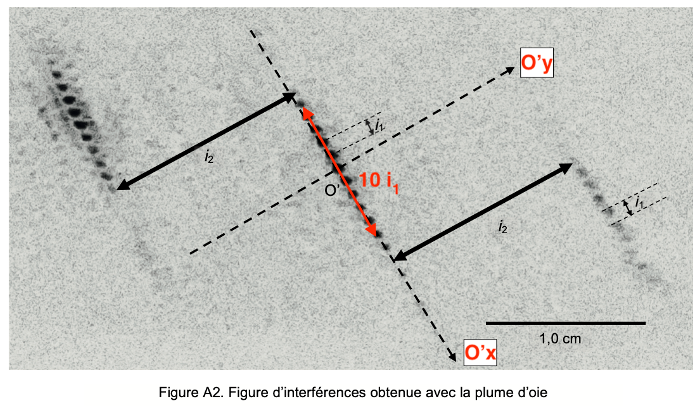
$$10\ i_1=\frac{3,8\times 1,0}{3,9}$$
$$10\ i_1=0,97\ cm$$
$$\ i_1=\frac{0,97\times{10}^{-2}\ }{10}$$
$$i_1=9,7\times{10}^{-4}\ m$$
$$i=\frac{\lambda\times D}{b}$$
$$i\times b=\lambda\times D$$
$$b=\frac{\lambda\times D}{i}$$
$$b_{barbule}=\frac{\lambda\times D}{i_2}$$
$$b_{barbule}=\frac{650\times{10}^{-9}\times 74\times{10}^{-2}}{1,3\times{10}^{-2}}$$
$$b_{barbule}=\ 3,7\times{10}^{-5}\ m$$
$$b_{barbe}=\frac{\lambda\times D}{i_1}$$
$$b_{barbe}=\frac{650\times{10}^{-9}\times 74\times{10}^{-2}}{9,7\times{10}^{-4}}$$
$$b_{barbe}=\ 5,0\times{10}^{-4}m$$
ANNEXE À RENDRE AVEC LA COPIE
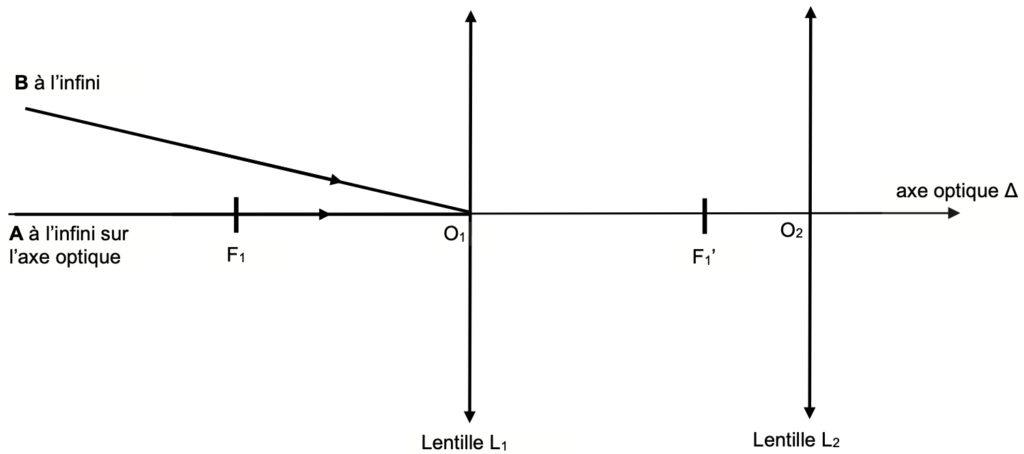
Figure A1. Schéma de la longue-vue (représentée sans souci d’échelle) assimilée à une lunette astronomique afocale
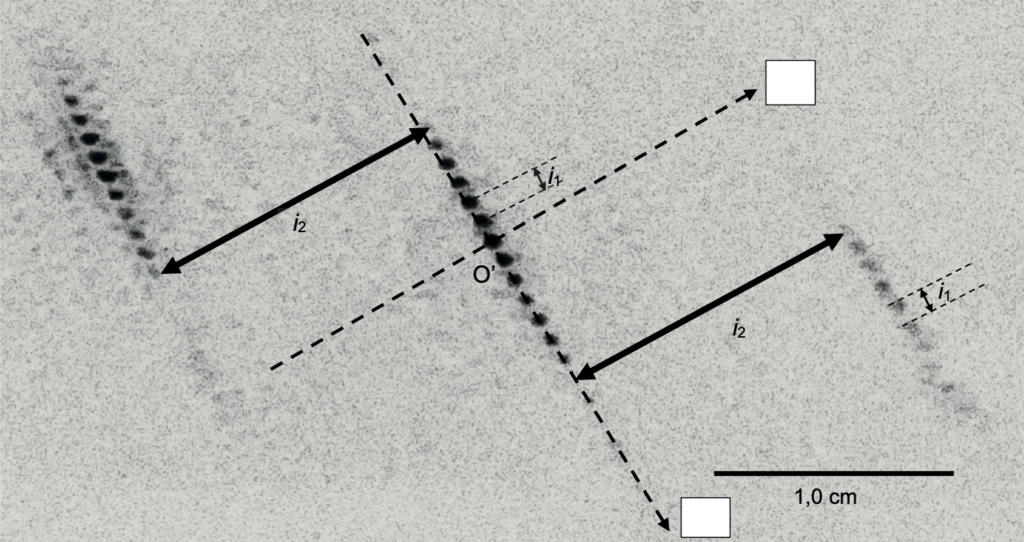
Figure A2. Figure d’interférences obtenue avec la plume d’oie
Il s’agit d’une photographie en négatif : les points sombres sur la photographie correspondent à des points brillants dans la réalité.
