Métropole Septembre 2022 Sujet 1
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1ME3
Sujet et corrigé
Mots-clés : lunette astronomique
Les anneaux de Saturne sont parmi les objets les plus fascinants et les plus accessibles à l’observation pour l’astronome amateur.

Selon la qualité de l’instrument d’observation, on peut distinguer plusieurs niveaux d’observation de cette planète. On présente en figure 1 les 4 premiers niveaux accessibles à l’astronome amateur :

Figure 1. Premiers niveaux d’observation des anneaux de Saturne
Dans cet exercice, on s’intéresse à une lunette astronomique commerciale et on cherche à déterminer quel niveau d’observation de Saturne elle permet d’atteindre.
Données :
- dans tout l’exercice on admet l’approximation des petits angles suivante valable pour tout angle α, exprimé en radian, très petit par rapport à 1 rad : tan α ≈ α ;
- la lunette astronomique étudiée possède un objectif de distance focale f1’= 700 mm et peut être associée à différents oculaires.
1. Modélisation optique de la lunette astronomique commerciale
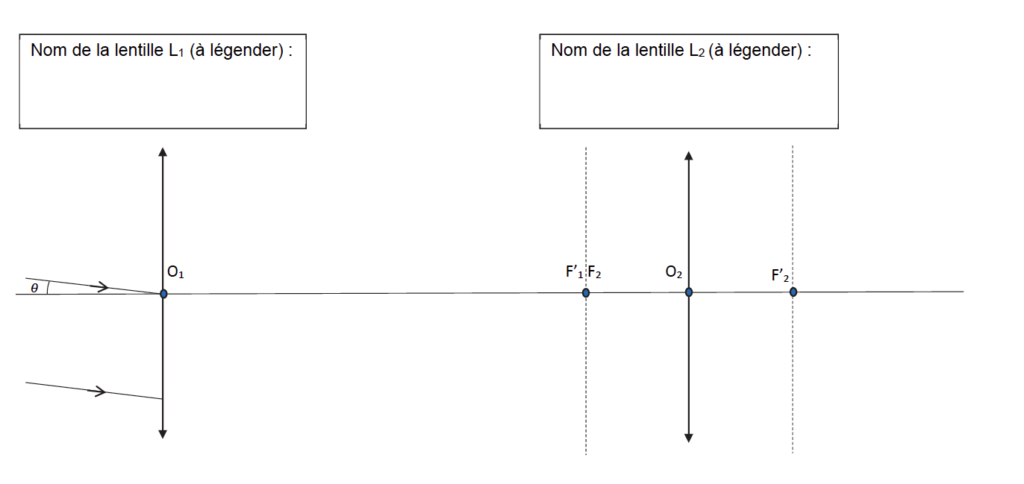
La lunette astronomique que l’on propose d’étudier est modélisée par deux lentilles minces convergentes, notées L1 et L2, possédant le même axe optique. La modélisation de cette lunette est proposée sur la figure de l’ANNEXE À RENDRE AVEC LA COPIE, où sont indiqués le foyer objet F2 de la lentille L2 et les foyers images F’1 et F’2 des deux lentilles.
Dans cette première partie, on s’intéresse aux trajets des rayons lumineux modélisant la propagation de la lumière dans la lunette. On note f2’ la distance focale de la lentille L2.
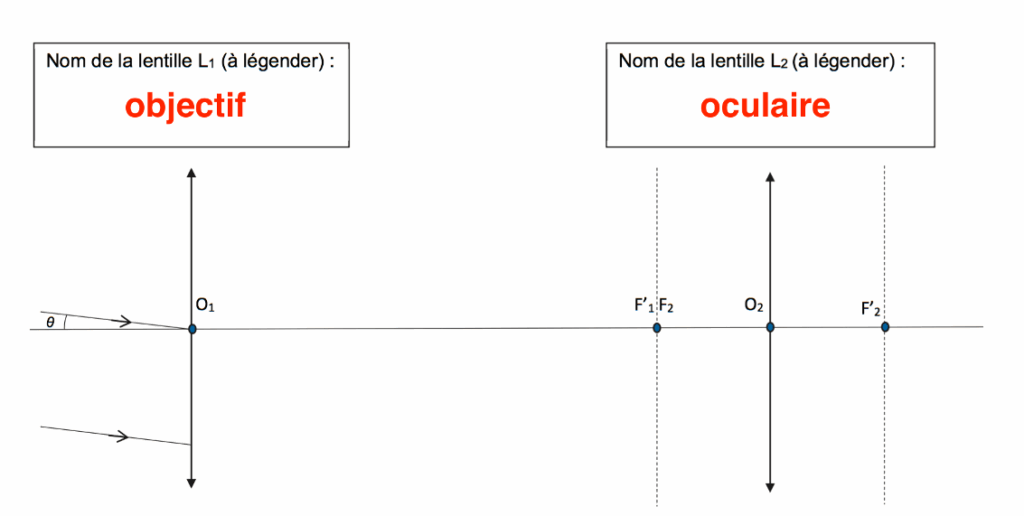
Q1. Indiquer, dans les cadres correspondant sur la figure de l’ANNEXE À RENDRE AVEC LA COPIE, les noms « objectif » et « oculaire ».
L1 : l’objectif car c’est une lentille convergente possédant une grande distance focale. C’est la lentille placée vers l’objet
L2 : l’oculaire car c’est une lentille convergente possédant une petite distance focale. C’est la lentille où on place l’œil.
Q2. Justifier que la lunette astronomique modélisée constitue un système optique afocal.
« Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini. »
La lentille L1, donne de l’objet $A_\infty B_\infty$, une image $A_1B_1$ sur le foyer image $F_1^\prime$.
Les deux foyers $F_1^\prime$ et $F_2$ sont confondus, ainsi la lentille L2, donne de l’objet $A_1B_1$, une image à l’infini.
La lunette est donc afocale.
Q3. Construire, sur la figure de l’ANNEXE À RENDRE AVEC LA COPIE, l’image d’un objet à l’infini vu sous un angle θ, formée par la lunette astronomique, en construisant l’image intermédiaire et en faisant apparaître l’angle θ’, angle sous lequel est vue l’image finale en sortie de lunette.
La lentille L1, donne de l’objet $A_\infty B_\infty$, une image $A_1B_1$ sur le plan focal.
Le rayon issu de B, passant par $O_1$ n’est pas dévié.
Le point $B_1$ est défini par l’intersection de ce rayon et le plan focal.
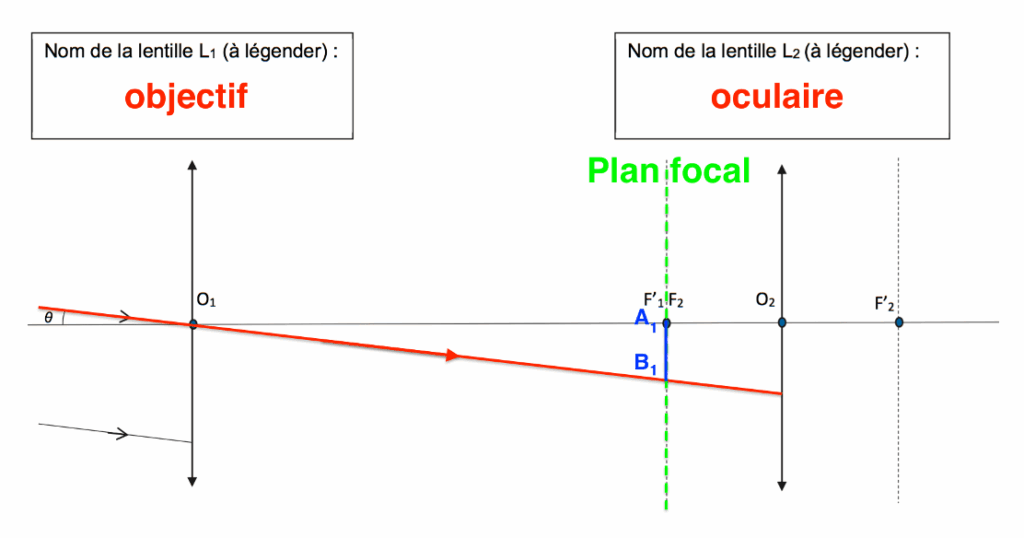
L’autre rayon est parallèle au premier. Il est dévié vers le point B1
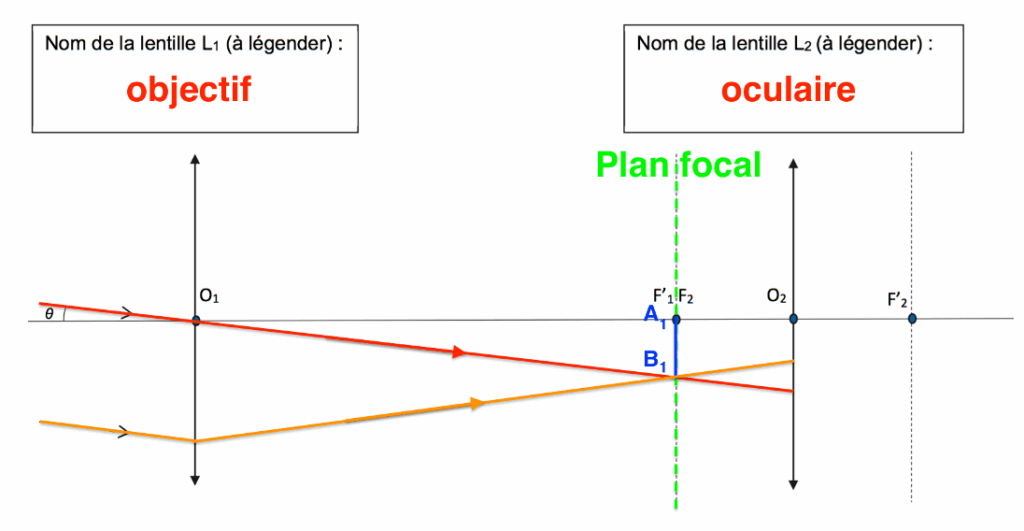
Un rayon issu de B1 passant par O2 n’est pas dévié.
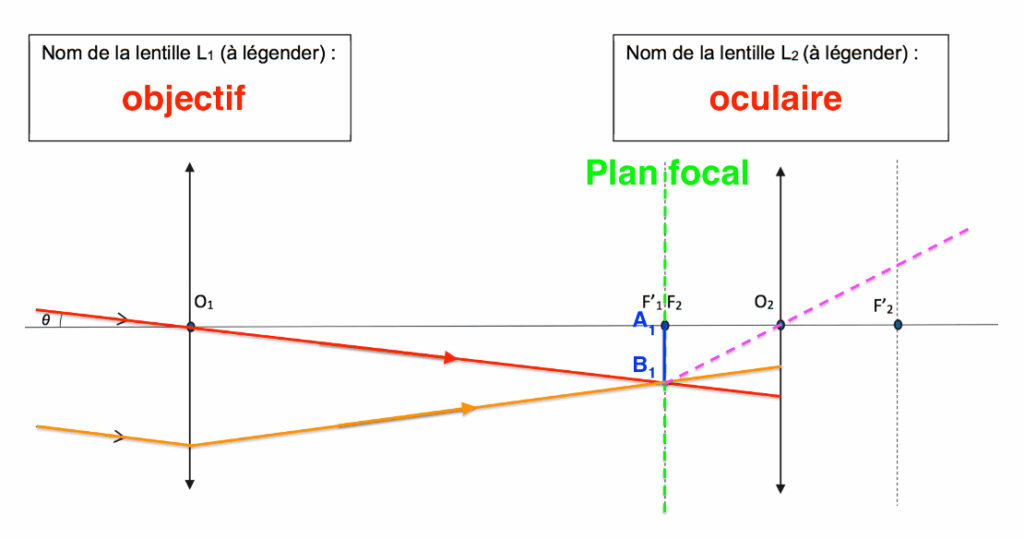
$A_1B_1$ étant sur le plan focal, il donnera une image à l’infini, tous les rayons issus de $B_1$, passant par la lentille L2 seront parallèles.
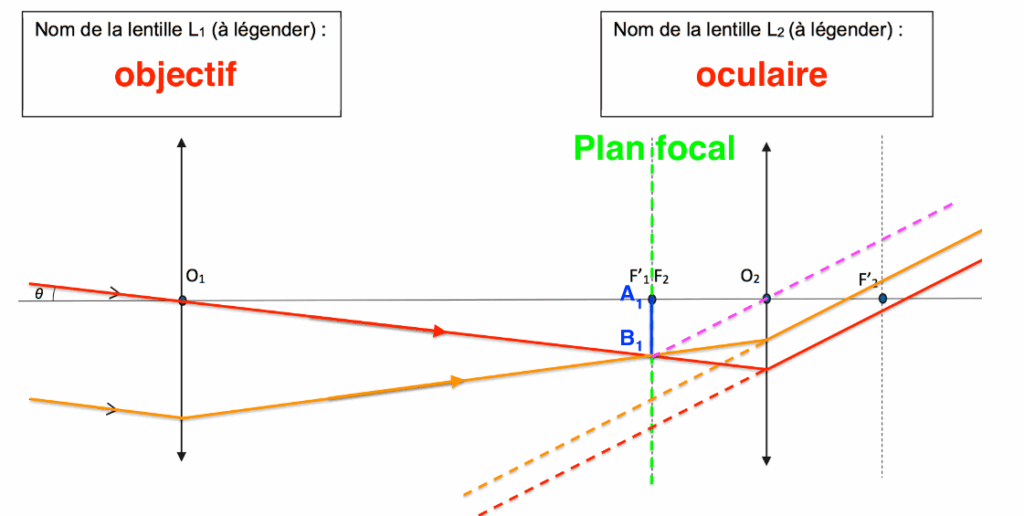
$\theta^\prime$ est l’angle sous lequel est vue l’image finale en sortie de lunette.
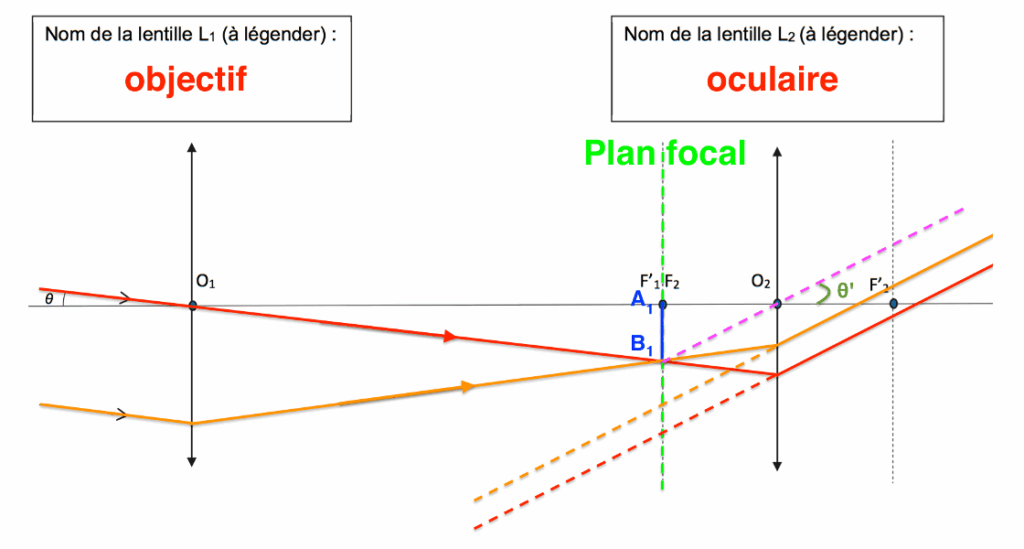
Q4. Donner la définition du grossissement G de la lunette astronomique en fonction des angles θ et θ’.
Le grossissement G est défini par :
$$G=\frac{\theta^\prime}{\theta}$$
Q5. Établir l’expression suivante du grossissement de la lunette astronomique : $G= \frac{f_1′}{f_2′} $
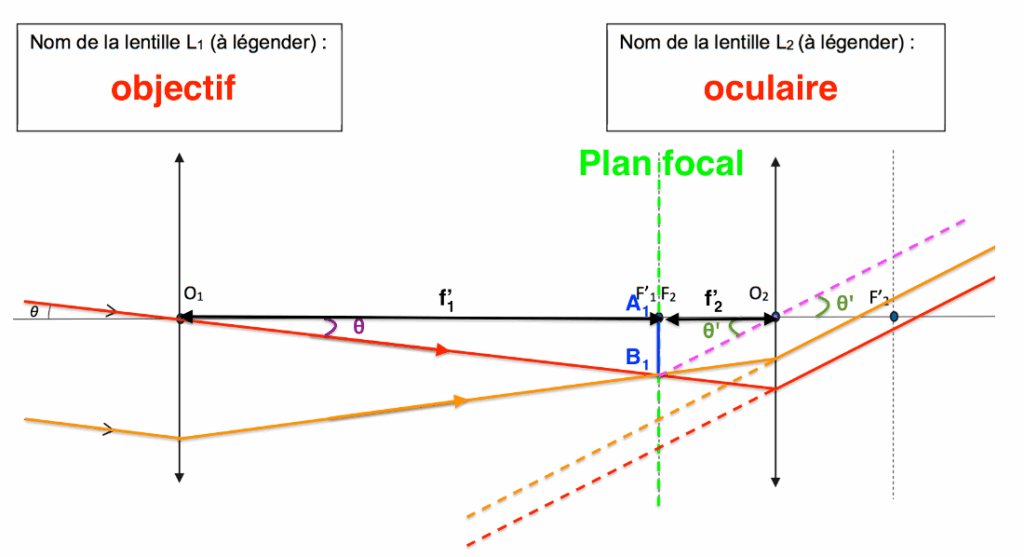
$$\tan(\theta)\approx\theta=\frac{A_1B_1}{f_1^\prime}$$
$$\tan(\theta^\prime)\approx\theta^\prime=\frac{A_1B_1}{f_2^\prime}$$
$$G=\frac{\theta^\prime}{\theta}=\frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}}=\frac{A_1B_1}{f_2^\prime}\times \frac{f_1^\prime}{A_1B_1}=\frac{f_1^\prime}{f_2^\prime}$$
Q6. En déduire la valeur de la distance focale f2’ de l’oculaire à choisir afin d’obtenir une lunette astronomique dont le grossissement est de 78.
$$G=\frac{f_1^\prime}{f_2^\prime}$$
$$G\times f_2^\prime=f_1^\prime$$
$$f_2^\prime=\frac{f_1^\prime}{G}$$
$$f_2^\prime=\frac{700.{10}^{-3}}{78}$$
$$f_2^\prime=9,0.{10}^{-3}\ m$$
$$f_2^\prime=9,0\ mm$$
2. Observation des anneaux de Saturne
On utilise la lunette astronomique de grossissement 78 modélisée dans la partie précédente pour observer Saturne et essayer de distinguer ses anneaux.
Données :
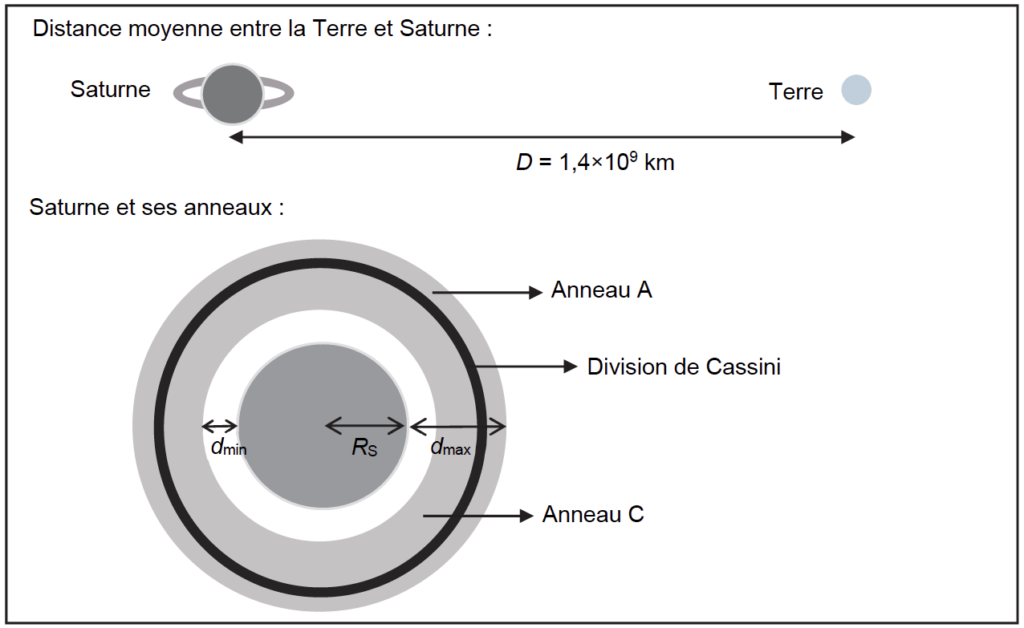
- distance moyenne entre les centres de la Terre et de Saturne : D = 1,4×109 km ;
- distance entre la surface de Saturne et l’extrémité la plus proche de l’anneau C (anneau le plus proche considéré visible) : dmin = 1,4×104 km ;
- distance entre la surface de Saturne et l’extrémité la plus éloignée de l’anneau A (anneau le plus éloigné considéré visible) : dmax = 7,7×104 km ;
- largeur de la division de Cassini : dcas = 4,8×103 km ;
- rayon de Saturne : RS = 5,8×104 km considéré comme faible devant D.
- angle minimal à partir duquel notre œil peut distinguer deux objets très proches : ε = 2,9×10-4 rad.
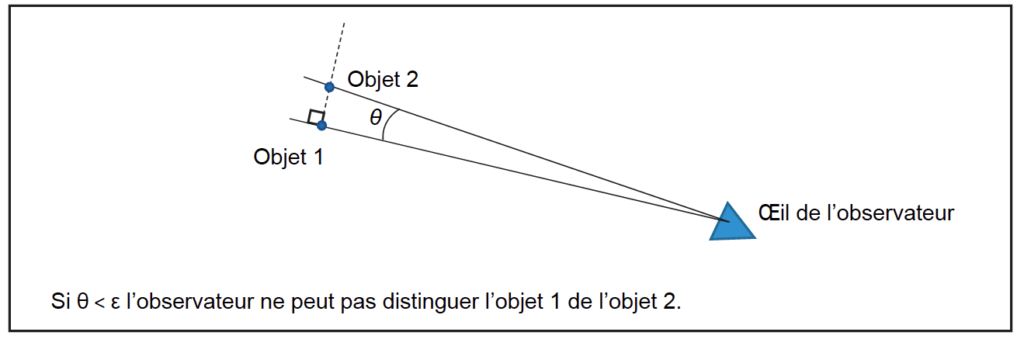
Q7. Décrire, en s’appuyant sur un calcul, comment apparaît Saturne à un observateur lors d’une observation à l’œil nu.
Considérons Saturne et l’extrémité la plus éloignée de l’anneau A (anneau le plus éloigné considéré visible), ils sont séparés de $d_{max}$.
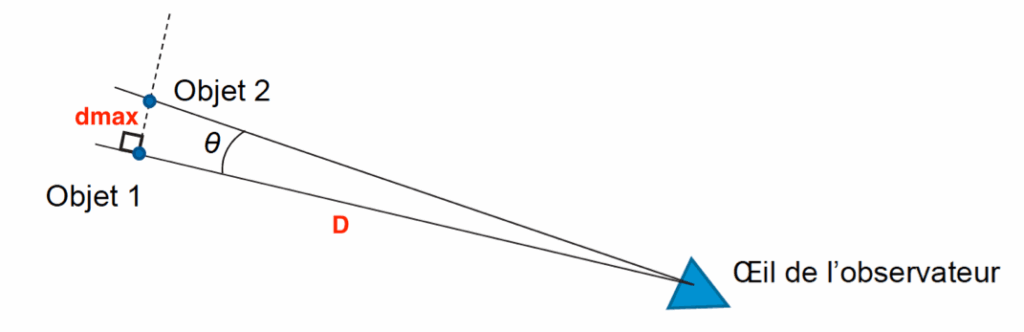
Calculons l’angle d’observation à l’œil nu :
$$\tan(\theta)\approx\theta=\frac{d_{max}}{D}$$
$$\theta=\frac{7,7\times {10}^4\times {10}^3}{1,4\times {10}^9\times {10}^3}$$
$$\theta=5,5\times {10}^{-5}\ rad$$
Angle minimal à partir duquel notre œil peut distinguer deux objets très proches : $\varepsilon=2,9\times {10}^{-4}\ rad$.
$\theta<\varepsilon$.
Nous ne pouvons distinguer les objets 1 et 2 : Saturne apparait Niveau 1 : anneaux non visibles.
Peut-on voir Saturne seul à l’œil nu ?
Considérons Saturne d’une extrémité à l’autre de distance $2R_S$.
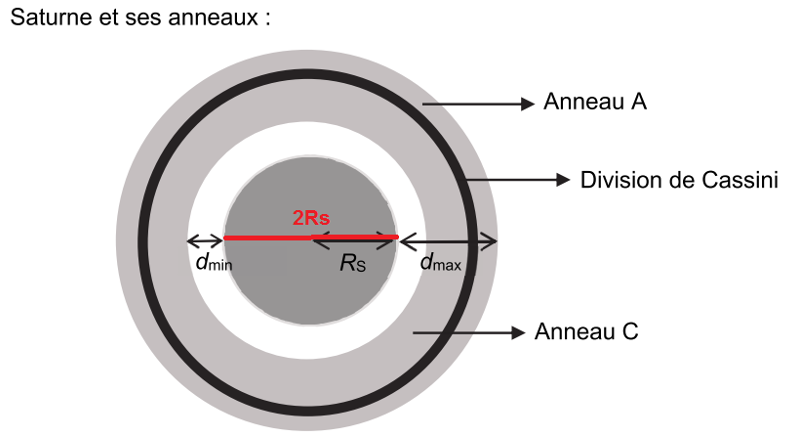
Calculons l’angle d’observation à l’œil nu :
$$\tan(\theta)\approx\theta=\frac{2R_S}{D}$$
$$\theta=\frac{2\times 5,8\times {10}^4\times {10}^3}{1,4\times {10}^9\times {10}^3}$$
$$\theta=8,3\times {10}^{-5}\ rad$$
Angle minimal à partir duquel notre œil peut distinguer deux objets très proches : $\varepsilon=2,9\times {10}^{-4}\ rad$.
$\theta<\varepsilon$.
Nous ne pouvons distinguer Saturne seul à l’œil nu.
Peut-on voir Saturne et ses anneaux à l’œil nu ?
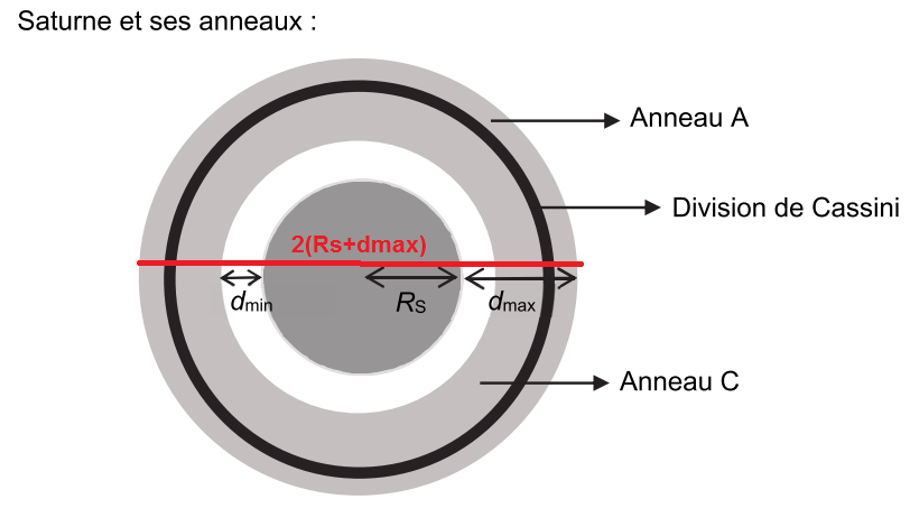
Considérons Saturne d’une extrémité à l’autre de distance $2(R_S+d_{max})$.
Calculons l’angle d’observation à l’œil nu :
$$\tan(\theta)\approx\theta=\frac{2(R_S+d_{max})}{D}$$
$$\theta=\frac{2\times (5,8\times {10}^4\times {10}^3+7,7\times {10}^4\times {10}^3)}{1,4\times {10}^9\times {10}^3}$$
$$\theta=1,9\times {10}^{-4}\ rad$$
Angle minimal à partir duquel notre œil peut distinguer deux objets très proches : $\varepsilon=2,9\times {10}^{-4}\ rad$.
$\theta<\varepsilon$.
Nous ne pouvons distinguer Saturne et ses anneaux à l’œil nu.
Conclusion : Saturne n’est pas visible à l’œil nu.
Q8. Déterminer le niveau d’observation de Saturne (figure 1) que l’on atteint avec la lunette astronomique utilisée.Le candidat est invité à prendre des initiatives et à présenter sa démarche même si elle n’a pas abouti. La démarche suivie est évaluée et nécessite donc d’être correctement présentée
On utilise la lunette astronomique de grossissement 78 modélisée dans la partie précédente pour observer Saturne et essayer de distinguer ses anneaux.
Considérons Saturne et l’extrémité la plus éloignée de l’anneau A (anneau le plus éloigné considéré visible).
$$\theta^\prime=78\times \theta$$
$$\theta^\prime=78\times 5,5\times {10}^{-5}$$
$$\theta^\prime=4,3\times {10}^{-3}\ rad$$
Angle minimal à partir duquel notre œil peut distinguer deux objets très proches : $\varepsilon=2,9\times {10}^{-4}\ rad$.
$\theta^\prime>\varepsilon$ : Nous pouvons distinguer les objets 1 et 2. Nous pouvons distinguer Saturne et l’extrémité la plus éloignée de l’anneau A.
Déterminons le niveau d’observation de Saturne (figure 1) que l’on atteint avec la lunette astronomique utilisée.
Considérons Saturne et l’extrémité la plus proche de l’anneau C (anneau le plus proche considéré visible).
Calculons l’angle d’observation à l’œil nu :
$$\tan(\theta)\approx\theta=\frac{d_{min}}{D}$$
$$\theta=\frac{1,4\times {10}^4\times {10}^3}{1,4\times {10}^9\times {10}^3}$$
$$\theta=1,0\times {10}^{-5}\ rad$$
$$\theta^\prime=78\times \theta$$
$$\theta^\prime=78\times 1,0\times {10}^{-5}$$
$$\theta^\prime=7,8\times {10}^{-4}\ rad$$
Angle minimal à partir duquel notre œil peut distinguer deux objets très proches : $\varepsilon=2,9\times {10}^{-4}\ rad$.
$\theta^\prime>\varepsilon$ : Nous pouvons distinguer les objets 1 et 2. Nous pouvons distinguer Saturne et l’extrémité la plus proche de l’anneau C. L’anneau C est visible.
Considérons la division de Cassini.
Calculons l’angle d’observation à l’œil nu :
$$\tan(\theta)\approx\theta=\frac{d_{cas}}{D}$$
$$\theta=\frac{4,8\times {10}^3\times {10}^3}{1,4\times {10}^9\times {10}^3}$$
$$\theta=3,4\times {10}^{-6}\ rad$$
$$\theta^\prime=78\times \theta$$
$$\theta^\prime=78\times 3,4\times {10}^{-6}$$
$$\theta^\prime=2,7\times {10}^{-4}\ rad$$
Angle minimal à partir duquel notre œil peut distinguer deux objets très proches : $\varepsilon=2,9\times {10}^{-4}\ rad$.
$\theta^\prime<\varepsilon$ : Nous ne pouvons pas distinguer les objets 1 et 2. Nous ne pouvons pas distinguer la division de Cassini.
Ainsi, le niveau d’observation de Saturne (figure 1) que l’on atteint avec la lunette astronomique utilisée est le Niveau 3 : anneaux visibles.
ANNEXE À RENDRE AVEC LA COPIE