Paiement sans contact

Asie 2025 Sujet 2

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°25-PYCJ2JA1

Apparu en France en 2012, le paiement sans contact permet de régler ses achats facilement et rapidement avec sa carte bancaire ou son téléphone portable. Placé à environ 4 cm du terminal de paiement, le circuit de la puce électronique intégré dans la carte reçoit un signal électromagnétique qui l’active. Le temps de réponse du circuit doit être de 1 à 2 secondes. Il est alors assez long pour permettre à la puce de transmettre un code identificateur au terminal sans être trop long pour l’utilisateur.

L’objectif de cet exercice est de modéliser une partie du circuit de la puce électronique et de vérifier que le modèle permet d’accéder au temps de réponse attendu.

Document — Modélisation électronique

Le circuit de la puce électronique présente sur une carte bancaire est modélisé selon le
schéma donné sur la figure 1 ci-dessous.

Figure 1 : Schéma du circuit électrique

Le conducteur ohmique de résistance $R = 100~\text{k}\Omega$ représente la résistance électrique de
la puce électronique.

Le générateur de tension $E = 5{,}0~\text{V}$ modélise l’antenne réceptrice de l’onde émise par le
terminal de paiement.

Lorsque la carte bancaire est suffisamment proche du terminal, un courant électrique
prend naissance dans le circuit. Ceci correspond à l’instant initial $t_0 = 0~\text{s}$ auquel
l’interrupteur $K$ est fermé. Le condensateur, de capacité $C = 40~\mu\text{F}$, se charge alors avec
une constante de temps notée $\tau$.

On considère que le temps de réponse du circuit électronique de la puce est $t_r = \tau$.

Q1- Exprimer l’intensité i(t) du courant circulant dans le circuit en fonction de la tension aux bornes du condensateur u_C et de la capacité C du condensateur.

$$i(t)=\frac{dq(t)}{dt}$$

$$q(t)=C\times U_C(t)$$

D’ou
$$i(t)=\frac{dC\times U_C(t)}{dt}$$
$$i(t)=C\times \frac{dU_C(t)}{dt}$$

Q2- Montrer que l’équation différentielle vérifiée par la tension u_C aux bornes du condensateur s’écrit :
$$ \frac{du_C}{dt} + \frac{u_C}{\tau} = \frac{E}{\tau}$$

où t est la constante de temps du circuit que l’on exprimera en fonction de R et de C.

D’après la loi d’additivité des tensions ou loi des mailles :

$$u_C(t)+u_R(t)=E$$

or $$u_R(t)=R\times i$$

$$u_C(t)+R\times i=E$$

Or
$$i(t)=C\times \frac{dU_C(t)}{dt}$$

$$u_C(t)+R\times C\times \frac{dU_C(t)}{dt}=E$$

On divise par RC
$$\frac{u_C(t)}{RC}+\frac{du_C(t)}{dt}=\frac{E}{RC}$$
$$\frac{du_C(t)}{dt}+\frac{u_C(t)}{RC}=\frac{E}{RC}$$

D’ou
$$\frac{du_C(t)}{dt}+\frac{u_C(t)}{\tau}=\frac{E}{\tau}$$
Avec $\tau=RC$

Q3- Vérifier que l’unité de $\tau$ est la seconde.

Analyse dimensionnelle :
$$\left[\tau\right]=\left[R\right]\left[C\right]$$

Avec
$$\left[R\right]=\frac{\left[U\right]}{\left[i\right]}$$

Et
$$\left[C\right]=\frac{\left[q\right]}{\left[U\right]}$$

$$\left[\tau\right]=\frac{\left[U\right]}{\left[i\right]}\frac{\left[q\right]}{\left[U\right]}$$
$$\left[\tau\right]=\frac{\left[q\right]}{\left[i\right]}$$

Avec $\left[i\right]=\frac{\left[q\right]}{\left[T\right]}$
$$\left[\tau\right]=\frac{\left[q\right]}{\frac{\left[q\right]}{\left[T\right]}}$$
$$\left[\tau\right]=\left[T\right]$$
$$\left[\tau\right]=s$$

L’unité de la constante τ est la seconde.

Q4- Vérifier que $u_C = E\cdot \left(1- \exp\left(-\frac{t}{\tau}\right)\right)$ est solution de l’équation différentielle ci-dessus.

Vérifions que la solution de cette équation différentielle est de la forme :
$$u_C(t)=E\times \left(1-e^{-\frac{t}{\tau}}\right)$$
-Dérivons $u_C(t)$ :
$$\frac{du_C(t)}{dt}=E\times (-1)\times \left(-\frac{1}{\tau}\right)\times e^{-\frac{t}{\tau}}$$
$$\frac{du_C(t)}{dt}=\frac{E}{\tau}\times e^{-\frac{t}{\tau}}$$

-Remplaçons $U_C(t)$ et $\frac{dU_C(t)}{dt}$ dans l’équation :
$$\frac{du_C(t)}{dt}+\frac{u_C(t)}{\tau}=\frac{E}{\tau}$$
$$\frac{E}{\tau}\times e^{-\frac{t}{\tau}}+\frac{E\times \left(1-e^{-\frac{t}{\tau}}\right)}{\tau}=\frac{E}{\tau}$$
$$\frac{E}{\tau}\times e^{-\frac{t}{\tau}}+\frac{E-E\times e^{-\frac{t}{\tau}}}{\tau}=\frac{E}{\tau}$$
$$\frac{E}{\tau}\times e^{-\frac{t}{\tau}}+\frac{E}{\tau}-\frac{E\times e^{-\frac{t}{\tau}}}{\tau}=\frac{E}{\tau}$$
$$\frac{E}{\tau}=\frac{E}{\tau}$$

Ainsi, $u_C(t)=E\times \left(1-e^{-\frac{t}{\tau}}\right)$ est solution de l’équation différentielle.

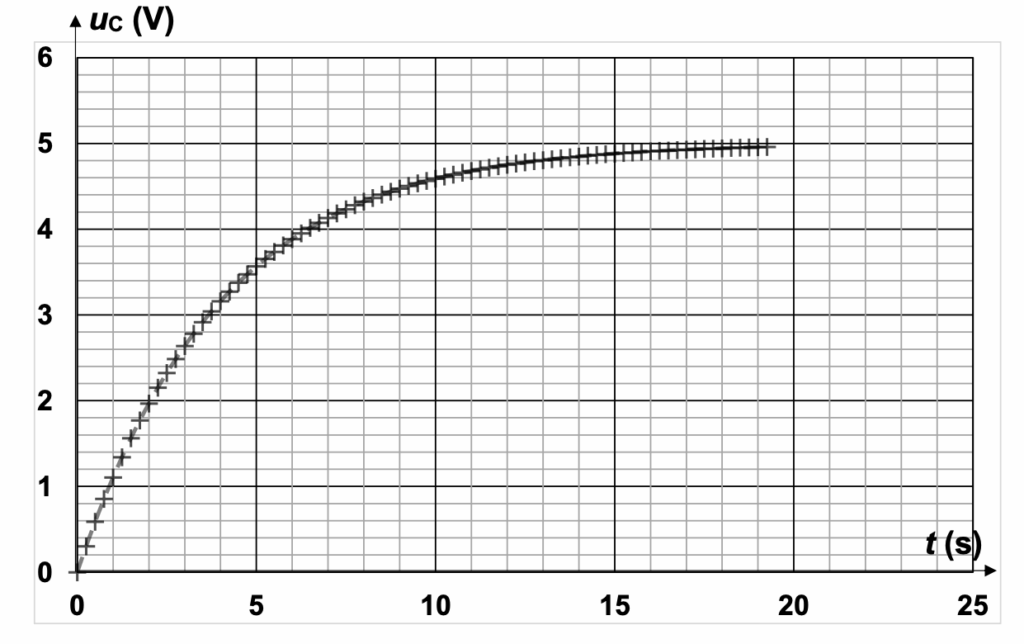
L’évolution de la tension u_C aux bornes du condensateur au cours de la charge est donnée sur l’ANNEXE p. 9 A RENDRE AVEC LA COPIE.

Q5- Déterminer, en explicitant la démarche choisie, la valeur de la constante de temps $\tau$.

$\tau$ peut être déterminée graphiquement par deux méthodes :
$u_C(\tau)=E\times \left(1-e^{-\frac{\tau}{\tau}}\right)=E\times \left(1-e^{-1}\right)=0,63E$
On trace la tangente à la courbe à $t=0$ et on regarde l’abscisse du point d’intersection entre cette tangente et l’asymptote $u_C=E$ pour la charge.

Q6- Indiquer, en justifiant, si le circuit électrique réalisé modélise correctement le circuit de la puce électronique d’une carte bancaire utilisée lors d’un paiement sans contact.

D’après le sujet :
« Le temps de réponse du circuit doit être de 1 à 2 secondes. Il est alors assez long pour permettre à la puce de transmettre un code identificateur au terminal sans être trop long pour l’utilisateur »
« On considère que le temps de réponse du circuit électronique de la puce est $t_r=\tau$. »

$t_r=\tau=4\ s$ : le temps de réponse est trop long pour l’utilisateur. Ainsi, le circuit électrique réalisé ne modélise pas correctement le circuit de la puce électronique d’une carte bancaire utilisée lors d’un paiement sans contact.

ANNEXE A RENDRE AVEC LA COPIE

Exercice 3 – Évolution de la tension u_C aux bornes du condensateur en fonction du temps – Courbe expérimentale obtenue au laboratoire