PARKER SOLAR PROBE

Bac Asie 2021 Sujet 1

Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée

Sujet n° 21-PYCJ1JA1

Le 12 août 2018, la NASA, l’agence spatiale américaine, a lancé en direction du Soleil une sonde spatiale,

PSP (Parker Solar Probe), dont la mission est d’étudier la couronne solaire. La sonde PSP doit relever de nombreux défis, notamment :

atteindre une orbite permettant d’approcher le Soleil de très près ;
protéger les instruments de mesure des rayonnements intenses.

**figure 1** – Sonde *PSP* (*Parker Solar Probe) Source : blogs.nasa.gov*

Partie 1 – Les caractéristiques orbitales de la sonde

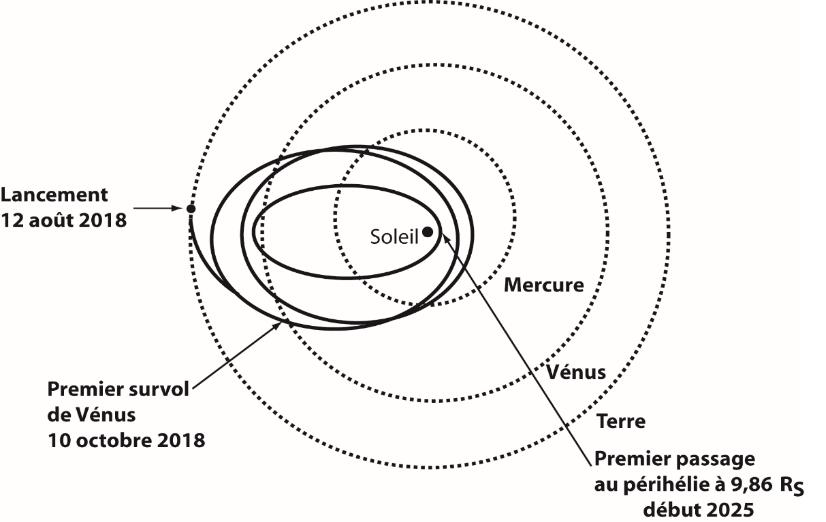
Depuis son lancement le 12 août 2018, la sonde PSP subit des modifications successives de son orbite autour du Soleil du fait de l’assistance gravitationnelle de la planète Vénus. Elle rejoint ainsi progressivement son orbite optimale qui lui permettra de passer au plus près du Soleil début 2025. La sonde effectuera alors quatre passages au périhélie P et pourra enregistrer un maximum de données expérimentales (figure 2 ci-dessous et figure 7 en annexe p. 16/16).

**figure 2** – Parcours de la sonde PSP *Source : blogs.nasa.gov*

Données :

– Masse du Soleil 𝑀_𝑆 = 2,0 × 10³⁰ kg

– Constante gravitationnelle G = 6,67 × 10⁻¹¹ m³⋅kg⁻¹⋅s⁻²

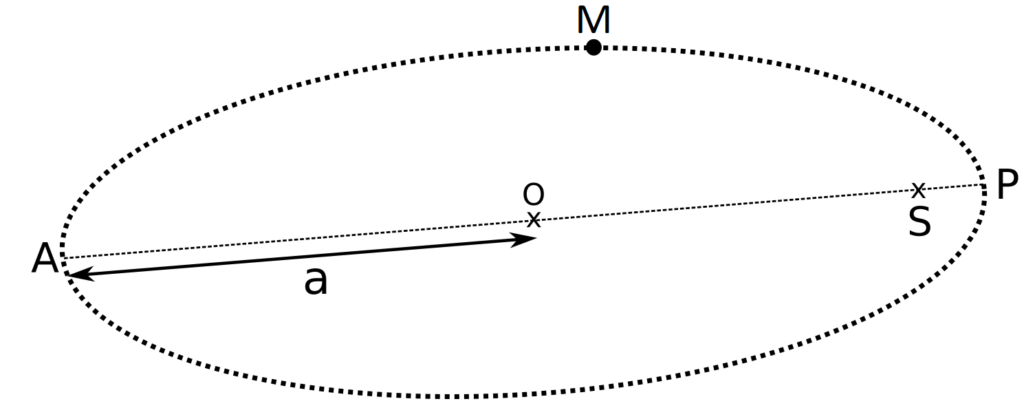
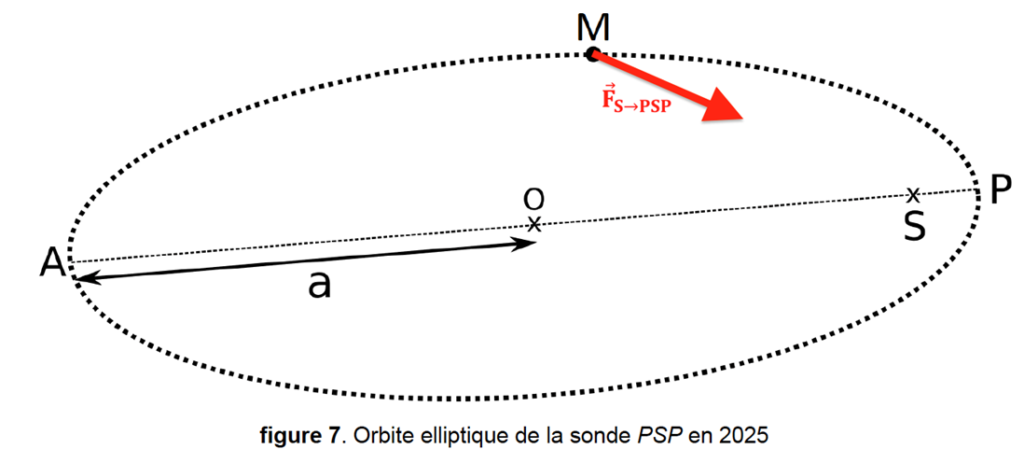
1. Sur la figure 7 EN ANNEXE À RENDRE AVEC LA COPIE page 16 / 16, on a représenté l’orbite elliptique que la sonde PSP décrira autour du Soleil en 2025. Les points A et P sont respectivement l’aphélie et le périhélie. Le point S représente le centre du Soleil.

1.1. Représenter sur la figure 7 EN ANNEXE À RENDRE AVEC LA COPIE page 16 / 16 et sans souci d’échelle, la force d’attraction gravitationnelle, notée $\overrightarrow{F}_{S \rightarrow PSP}$ , modélisant l’action exercée par le Soleil sur la sonde PSP lorsqu’elle est au point M.

Réponse :

1.2. En utilisant la 2^ème loi de Kepler, comparer la valeur v_𝑃 de la vitesse de la sonde au point P à la valeur v_A de la vitesse de la sonde au point A.

Réponse :

2^ème loi de Kepler : Le segment soleil planète balaie des aires égales au cours de durées égales

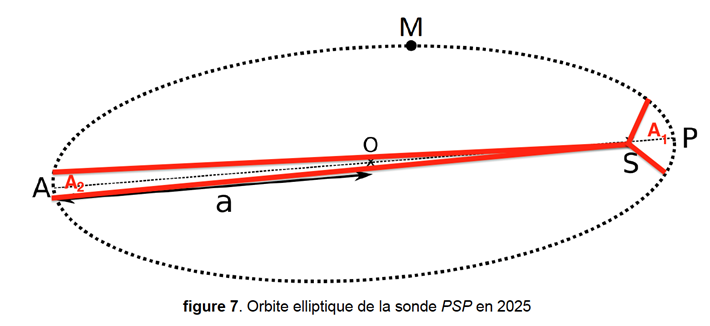
Pour que A₁=A₂, il faut que d_A<d_P

d_A/∆t<d_P/∆t

v_A<v_P

2. La NASA prévoit que la valeur v_𝑃 de la vitesse de la sonde au point P sera de 192 km⋅s⁻¹ avec une incertitude-type de l’ordre de 5 km⋅s⁻¹.

On souhaite savoir si cette valeur de la vitesse a été déterminée à l’aide du modèle du mouvement circulaire pour la sonde PSP sur son orbite autour du soleil ou si un autre modèle a été utilisé.

On se propose donc de déterminer la valeur v de la vitesse de la sonde PSP en supposant que son mouvement est circulaire, de rayon 𝑟 = SP = 6,9 × 10⁶ km, afin de la comparer à celle prévue par la NASA (figure 3). Le référentiel héliocentrique est considéré comme galiléen.

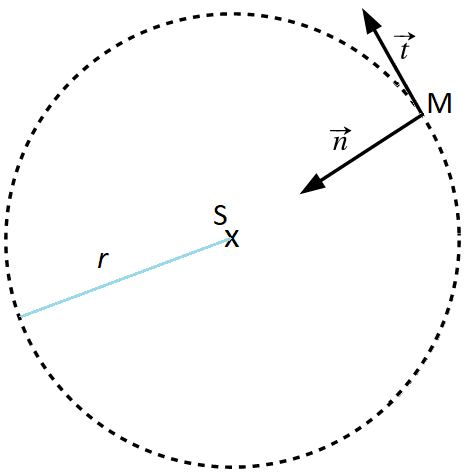
figure 3 – Modèle du mouvement circulaire de la sonde PSP et repère de Frenet

2.1. À l’aide de la 2e loi de Newton, montrer que, dans le cas d’une trajectoire circulaire, la vitesse v de la sonde PSP est constante et a pour expression :

$v= \sqrt{\frac{G \times M_S}{r}}$

avec 𝑀_𝑆 la masse du Soleil et 𝑟 le rayon de la trajectoire circulaire.

Réponse :

Système : sonde PSP

Référentiel : Héliocentrique galiléen

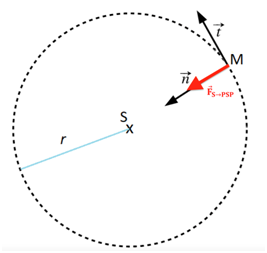
$\sum_{}^{}\overrightarrow{F_{ext}}=m\overrightarrow{a}$

$\overrightarrow{F}_{S/PSP}=m_{PSP}\overrightarrow{a}_{S}$

$G\times \frac{m_{PSP}\times M_{S}}{r^2}\overrightarrow{n}=m_{PSP}\overrightarrow{a}$

$\overrightarrow{a}=G\times \frac{M_{S}}{r^2}\overrightarrow{n}$

Or, pour un mouvement circulaire, dans la base de Frenet, le vecteur accélération est de la forme :

$\vec{a}=\frac{v^2}{r}\vec{n}+\frac{dv}{dt}\vec{t}$

L’accélération étant unique, par identification :

$\frac{v^2}{r}=G\ \times \frac{M_S}{r^2}$

donc

$v=\sqrt{\frac{G\times M_{S}}{r}$

2.2. Calculer la valeur v de la vitesse de la sonde PSP dans le cadre de ce modèle.

Réponse :

$v=\sqrt{\frac{G\times M_{S}}{r}$

$v=\sqrt{\frac{6,67\times 10^{-11}\times 2,0 \times 10^{30}}{6,9\times 10^{9}}$

$v=1,4 \times 10^{5} m.s^{-1}$

$v=1,4 \times 10^{2} km.s^{-1}$

2.3. Apporter une conclusion à la problématique posée dans cette question 2.

Réponse :

v≠v_modèle

Donc la vitesse à été déterminée à l’aide d’un autre modèle.

La 3^ème loi de Kepler lie le demi-grand axe orbital et la période de révolution des systèmes (planète, sonde) en orbite autour du Soleil. On peut ainsi déterminer la période de révolution de la sonde PSP autour du Soleil à partir de la mesure du demi-grand axe de sa trajectoire elliptique.

3. En utilisant la 3ème loi de Kepler et après analyse du programme Python figurant ci-après et de ses résultats, déterminer la période de révolution T de la sonde PSP autour du Soleil.

Caractéristiques des orbites des planètes et de la sonde PSP autour du soleil

Planète	Mercure	Vénus	Terre	Mars	Jupiter	Saturne	Uranus	Neptune	Sonde *PSP*
Demi- grand axe orbital (× 10^𝟑 𝐤𝐦)	57909,23	108209,5	149597,8875	227944	778340	1426700	2870700	4498400	𝑎 = 58210
Période de révolution (j) (jour)	87,95565	224,667	365,2564	686,885	4332,01	10754	30698	60216,8	T

Le programme Python ci-dessous a été écrit à partir des caractéristiques des orbites des planètes.

1 import numpy as np

2 import statsmodels.api as sm

4 # Périodes T (en j)

5 T = np.array([ 87.95565, 224.667, 365.256363, 686.885, 4332.01,

6 10754, 30698, 60216.8 ])

8 # Demi-grands axes a (en km)

9 a = np.array([ 57909230, 108209500, 149597887.5, 227944000,

10 778340000, 1426700000, 2870700000, 4498400000 ])

12 # sm.OLS(y, x) définit un modèle linéaire de la forme y = kx

13 model = sm.OLS(T**2, a**3)

15 # model.fit() calcule le coefficient k

16 results = model.fit()

18 print(“— Résultats de la modélisation —\n”)

20 # Affiche la valeur du coefficient k

21 print(” k=”, results.params[0], (” j**2 * km**-3″)

Affichage des résultats du programme à l’écran :

— Résultats de la modélisation —

k= 3.983462498345611e-20 j**2 * km**-3

Remarque : la notation e-20 signifie 10^-20.

Réponse :

3^ème loi de Kepler : $\frac{T^{2}}{a^{3}=constante}$

D’après la modélisation du programme Python, l’équation est de la forme T²=ka³

$T=\sqrt{ka^3}$

$T=\sqrt{3,983462498345611\times 10^{-20}(58210\times 10^3)^3}$

$T=88,3 jours$

Partie 2 – Les panneaux photovoltaïques

Durant la mission, les panneaux photovoltaïques de la sonde PSP servent à fournir l’énergie électrique nécessaire au fonctionnement des instruments de mesure embarqués. Ils permettent d’obtenir une puissance électrique utile P_el= 340 W.

En 2025, au plus près du Soleil, ils devront être refroidis. Une puissance thermique P_th devra alors être évacuée grâce à de l’eau sous pression circulant entre les panneaux photovoltaïques et des radiateurs (figure 4). Lorsque le bouclier sera parfaitement orienté vers le Soleil, la puissance thermique à évacuer P_th sera 13 fois supérieure à la puissance électrique utile ; une erreur d’inclinaison du bouclier thermique de 1° entrainera une puissance thermique supplémentaire à dissiper de 35%.

Dans les questions suivantes, on se place dans le cas critique d’une erreur de 1° d’inclinaison du bouclier thermique.

Données :

Masse volumique de l’eau liquide dans les conditions de pression et de température de la sonde PSP : 𝜌_eau = 0,958 kg ⋅ L−1.

Durée du passage à proximité du Soleil : Δt = 110 ℎ
Pression de l’eau dans le circuit : 5 bar
Température d’ébullition de l’eau sous 5,0 bar : T_éb = 150°C
Capacité thermique massique de l’eau : 𝐶_eau = 4185 J ⋅ K⁻¹⋅kg⁻¹

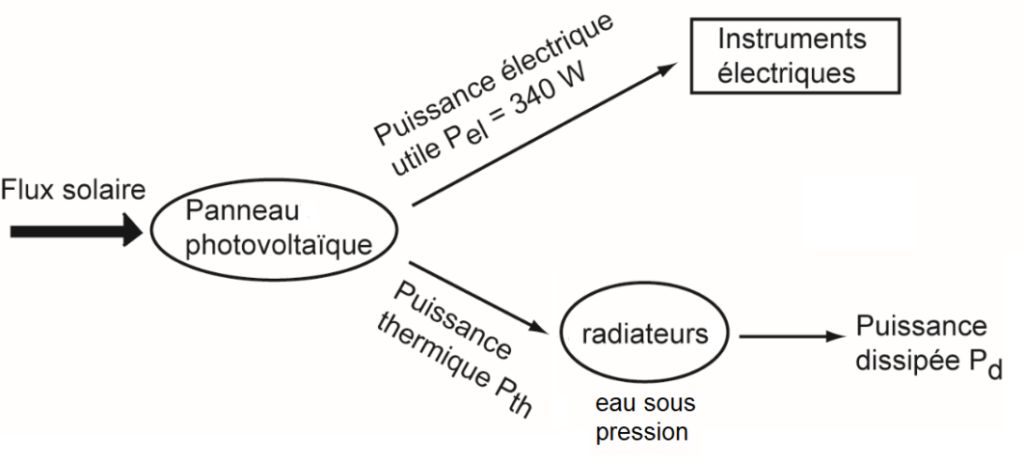
**figure 4** – Diagramme énergétique de l’alimentation électrique de la sonde *PSP*

4. Sachant que les radiateurs peuvent dissiper une puissance maximale P_d,max = 6000 W, montrer que ces radiateurs peuvent effectivement dissiper la puissance thermique cédée par les panneaux photovoltaïques à l’eau sous pression.

Réponse :

«La puissance thermique à évacuer sera 13 fois supérieure à la puissance électrique utile.

Une erreur d’inclinaison du bouclier thermique de 1° entrainera une puissance thermique supplémentaire à dissiper de 35%…. on se place dans le cas critique d’une erreur de 1° d’inclinaison du bouclier thermique »

$P_{Th}=13\times P_{el}\times 1,35$

$P_{Th}=13\times 340 \times 1,35$

$P_{Th}=5967 W$

$P_{Th}<P_{d,\max }=6000\ W$

Ces radiateurs peuvent effectivement dissiper la puissance thermique cédée par les panneaux photovoltaïques à l’eau sous pression.

Pendant la durée Δt du passage à proximité du Soleil, l’équivalent d’un volume d’eau 𝑉_eau = 7 570 L va circuler pour refroidir les panneaux solaires. La température de ce volume d’eau va passer de la valeur T_min = 50°C à une valeur maximale T_max que l’on cherche à déterminer.

On considère ici que la puissance thermique reçue par ce volume d’eau est P_th,max = 6 000 W.

5. Donner l’expression de l’énergie thermique Q_R reçue par l’eau en fonction de P_th,max et Δt.

Réponse :

$Q_{R}=P_{Th,max}\times \Delta t$

6. En supposant que l’élévation de température du volume total d’eau est uniquement due aux panneaux solaires, déterminer la température T_max atteinte et déterminer si le système de refroidissement risque ou non l’explosion.

Le candidat est invité à prendre des initiatives et à exposer sa démarche même si elle n’est pas complètement aboutie.

Réponse :

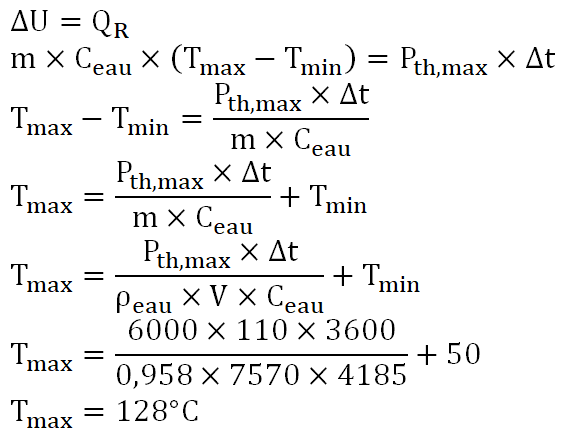
Le système de refroidissement risque l’explosion si l’eau se transforme en vapeur. La température d’ébullition de l’eau dans ces conditions est de 150°C. T_max<150°C, le système ne risque pas d’exploser.

Partie 3 – Le bouclier thermique

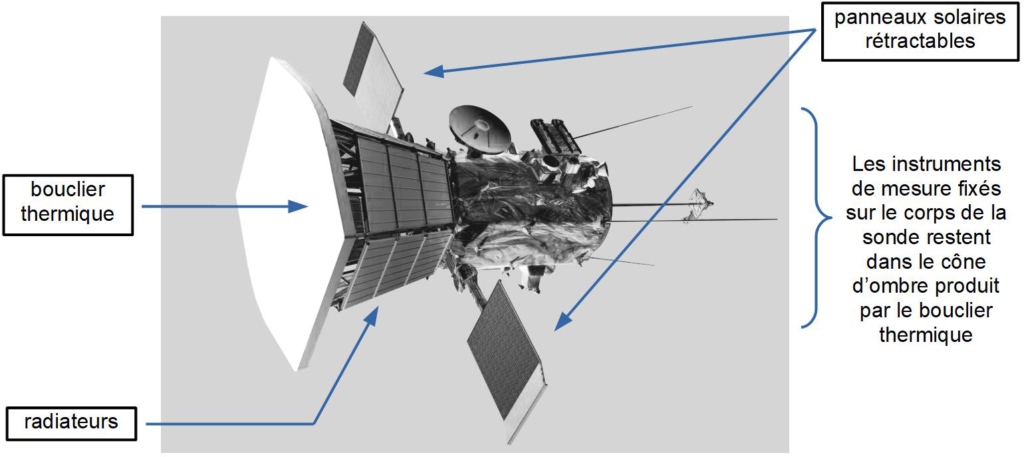
La sonde PSP est protégée des rayonnements solaires par un bouclier thermique de surface S_b et d’épaisseur e (figures 1 et 5). Constamment tourné vers le Soleil, ce bouclier thermique permet de garder l’ensemble du corps de la sonde à une température convenable pour ne pas endommager les instruments embarqués.

Le bouclier thermique est composé d’un revêtement externe à base d’alumine, capable d’endurer de hautes températures jusqu’à 1900 K. Derrière ce revêtement, se trouve de la mousse de carbone, prise entre deux couches rigides en fibre de carbone, très résistantes à la température et à la déformation (figure 5).

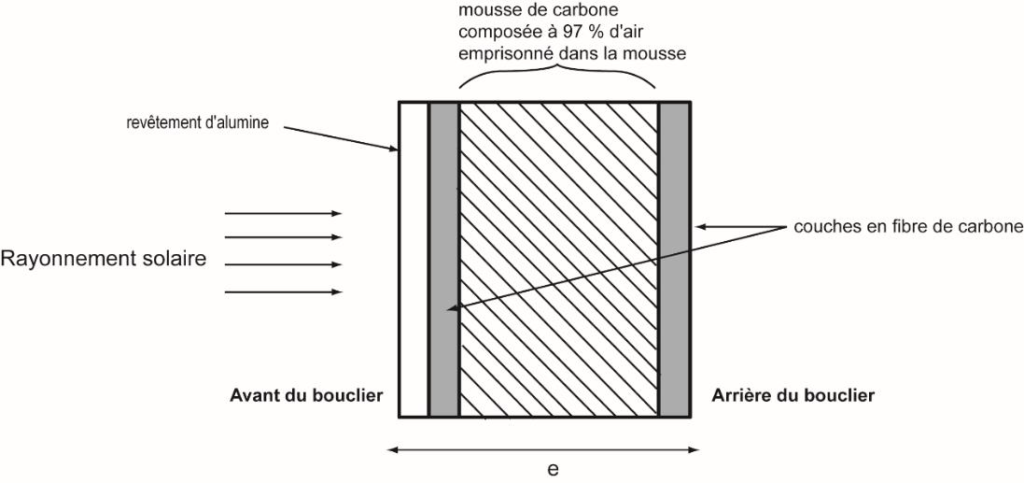
**figure 5** – Schéma simplifié du bouclier thermique vu en coupe

Soumis à l’intense rayonnement du Soleil, la température à l’avant du bouclier atteint une valeur

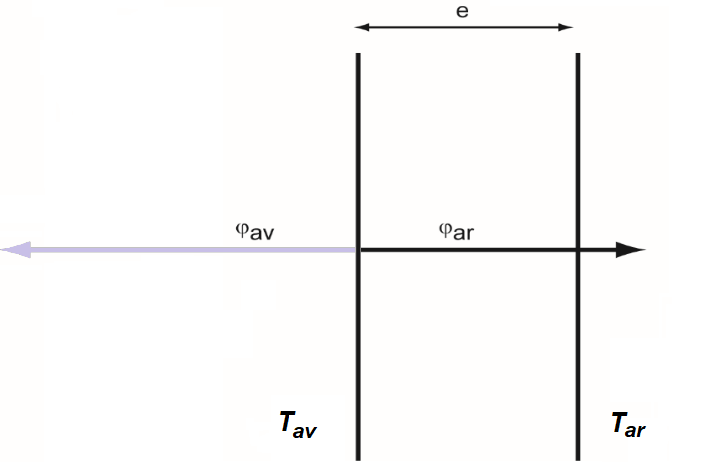
T_av = 1700 K et rayonne un flux thermique surfacique important 𝜑_av. Par ailleurs, un flux thermique surfacique 𝜑_av = 1,55 kW⋅m⁻² traverse la surface S_b du bouclier vers l’arrière (figure 6). Pour permettre le bon fonctionnement de la sonde, il est impératif de limiter l’élévation de température à l’arrière du bouclier thermique en dépit de ce flux thermique surfacique élevé.

**figure 6** – Flux thermiques au niveau du bouclier thermique

Données :

Conductivités thermiques de quelques matériaux :

Matériau	Mousse de carbone	Alumine	Métaux	PVC
Conductivité thermique (W⋅m⁻¹⋅K⁻¹)	0,0262	37	20 à 400	0,17

Caractéristiques du bouclier thermique :
- surface : S_b = 16,6 m²
- épaisseur : e = 11,4 cm
- conductivité thermique du bouclier thermique : 𝜆 = 0,140 W⋅m⁻¹⋅K⁻¹
Résistance thermique R_th d’une paroi de surface S, d’épaisseur s et de conductivité thermique 𝜆 :

$R_{th}= \frac{e}{\lambda \times S}$ (en K⋅W⁻¹)

Flux thermique Φ traversant une paroi de résistance thermique R_th et soumise à une différence de température |ΔT| :

$\Phi= \frac{\lvert \Delta T \rvert}{R_{th}}$

7. Caractériser le mode de transfert thermique entre le Soleil et la sonde PSP.

Réponse :

Rayonnement

8. Justifier l’utilisation de la mousse de carbone à l’intérieur du bouclier thermique.

Réponse :

On cherche à avoir une grande résistance thermique.

de la mousse de carbone est très petit.

$R_{th}= \frac{e}{\lambda \times S}$

Donc sa résistance thermique est très grande.

9. Déterminer la valeur du flux thermique total vers l’arrière Φ.

Réponse :

$\phi_{ar}=\varphi_{ar}\times S$

$\phi_{ar}=1,55\times 10^{3}\times 16,6$

$\phi_{ar}=2,57\times 10^{4} W$

10. À l’aide des caractéristiques du bouclier thermique et des données, déterminer l’écart de température |ΔT| entre les deux faces du bouclier thermique ainsi que la température T_ar à l’arrière du bouclier.

Commenter

Le candidat est invité à prendre des initiatives et à exposer sa démarche même si elle n’est pas complètement aboutie.

Réponse :

$\Delta T = \phi_{ar} \times R_{Th}$