Photographie à l’aide d’une lentille boule

E3C2 – 10 points – Durée 1h – calculatrice autorisée

À bord de la station spatiale internationale (I.S.S.) les passagers se sont amusés à réaliser la photographie 1 ci-dessous où l’on peut observer l’image du visage d’un astronaute à travers une bulle d’eau.

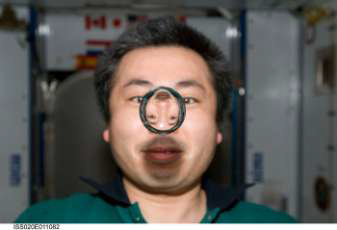
Photographie 1 : le japonais Koichi Wakata observe une goutte d’eau en lévitation à bord de l’ISS.

D’après : http://www.esa.int/spaceinimages/Images/2009/06/Japan_Aerospace_Exploration_Agency_JAXA_astronaut_Koichi_Wakata (2009)

On souhaite reproduire au laboratoire cette photographie insolite en remplaçant la bulle d’eau par une lentille mince convergente (L) et en utilisant un personnage en bois.

Afin de réaliser cette reproduction au laboratoire, on se propose de :

modéliser la situation photographiée à bord de la station spatiale ;
déterminer certains paramètres de la situation réalisée au laboratoire.

Données :

relation de conjugaison pour une lentille mince :

$\frac{1}{\overline{OA'}}-\frac{1}{\overline{OA}}=\frac{1}{\overline{OF'}}$

relation de grandissement γ pour une lentille mince :

$\gamma=\frac{\overline{OA'}}{\overline{OA}}=\frac{\overline{A'B'}}{\overline{AB}}$

où f’ est la distance focale de la lentille, O le centre optique de la lentille, AB l’objet et A’B’ l’image de AB à travers la lentille ;

indice de réfraction de l’eau : n_eau = 1,33.

Détermination de la distance focale de la bulle d’eau

Pour reproduire cette expérience, il faut évaluer la valeur de la distance focale d’une bulle d’eau qui constitue une lentille boule de distance focale f’ = OF’ (en m) qui se comporte en première approximation comme une lentille mince. Cette distance focale donnée par la relation :

$f'=OF'=\frac{n \times R}{2 \times (n-1)}$

où n est l’indice de réfraction du matériau constituant la lentille boule, R est son rayon, O le centre de la lentille boule et F’ le foyer image de celle-ci.

En considérant que la bulle d’eau possède un diamètre de l’ordre de 5 cm, déterminer la valeur de sa distance focale.

Modélisation de la situation photographiée dans la station spatiale

On considère qu’une bulle d’eau se comporte comme une lentille mince convergente. La proposition de la modélisation de la situation à bord de la station spatiale est donnée ci-après.

AB représente une petite partie du visage de l’astronaute et A’B’ est l’image de AB à travers la lentille. Le schéma présente les éléments principaux de la situation, sans respecter d’échelle.

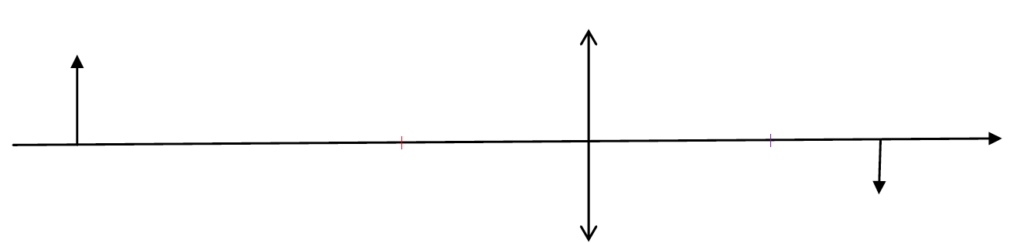
2. Pour le schéma ci-dessus, qualifier l’image représentée avec deux des termes suivants : image réelle, image virtuelle, image droite, image renversée.

3. Sans calcul, montrer que le schéma ci-dessus modélise correctement la situation photographiée à bord de la station spatiale.

Choix d’une lentille mince pour modéliser la bulle d’eau

Pour reproduire la situation de la station spatiale, un groupe d’élèves décide d’utiliser une lentille mince convergente de grand diamètre afin de remplacer la bulle d’eau de la station spatiale. On dispose au laboratoire d’une telle lentille (L) mais sa distance focale f’ est inconnue.

Pour déterminer la valeur de la distance focale de cette lentille, les élèves effectuent une série de mesures : pour différentes positions de la lentille par rapport à l’objet, ils déplacent l’écran pour former une image nette sur celui-ci, puis ils mesurent les valeurs algébriques $\overline{OA}$ et $\overline{OA'}$ .

Tableau de mesures

Point de mesure n°	1	2	3	4	5	6
$\overline{OA}$ en m	− 0,150	− 0,200	− 0,300	− 0,400	− 0,500	− 0,600
$\overline{OA'}$ en m	0,762	0,307	0,218	0,178	0,161	0,158
Point de mesure n°	7	8	9	10	11
$\overline{OA}$ en m	− 0,700	− 0,800	− 0,900	− 1,000	− 5,0
$\overline{OA'}$ en m	0,153	0,147	0,146	0,143	0,126

Les élèves placent alors, après calculs, les points de mesure sur un grapheet tracent en effectuant une régression linéaire la courbe de tendance (en pointillés) dont l’équation y = f(x) s’affiche ci-après.

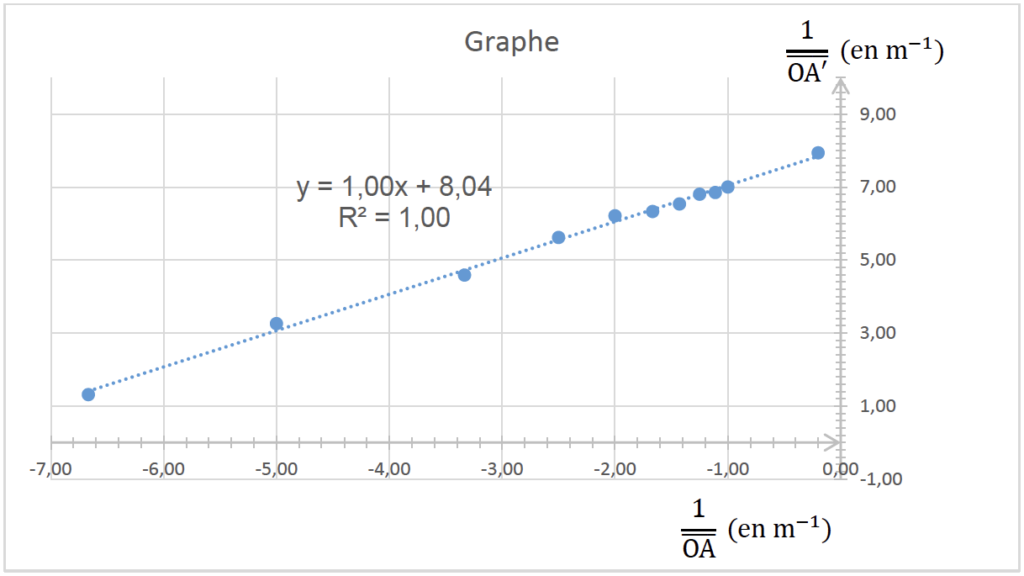
Graphe avec y = $\frac{1}{\overline{OA'}}$ en ordonnée (en m^-1) et x = $\frac{1}{\overline{OA}}$ en abscisse (en m^-1)

4. Les résultats expérimentaux obtenus sont-ils en accord avec la relation de conjugaison d’une lentille mince, fournie dans les données ? Justifier.

5. Déterminer la valeur de la distance focale f’ de la lentille (L).

6. Conclure sur le fait que cette lentille puisse être utilisée ou non pour remplacer la bulle d’eau étudiée à la question 1.

7. Justifier, en choisissant deux propositions parmi celles ci-dessous, que le point de mesure n° 11 permet d’estimer sans calcul la valeur de la distance focale de la lentille mince (L). Préciser cette valeur.

(a) L’image est à l’infini par rapport à la lentille

(b) L’objet est à l’infini par rapport à la lentille

(c) L’objet est dans le plan focal objet de la lentille

(d) L’image est dans le plan focal image de la lentille

Reproduction de la situation au laboratoire

Le groupe d’élèves a ainsi reproduit au laboratoire la situation de la station spatiale en remplaçant la bulle d’eau par une lentille mince convergente (L) de grand diamètre (10,0 cm) et de distance focale f’ dont la valeur sera assimilée à celle de la question 7 soit f’ = 0,126 m. L’astronaute est remplacé par un personnage en bois de hauteur 44,0 cm dont le visage mesure 8,5 cm de haut. Un premier essai figure sur la photographie 2.

Lors de la prise de vue, la distance entre la lentille (L) et le personnage est de 33,0 cm.

**Photographie 2 :** première expérience réalisée au laboratoire

8. À l’aide des informations sur les conditions dans lesquelles la photographie 2 a été réalisée, déterminer par le calcul la valeur de la position et la taille de l’image du personnage à travers la lentille.