E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02721 , n°G1SPHCH02731 et n°G1SPHCH02778
Télécharger l’exercice en PDF :
On appelle « générateur photovoltaïque » un assemblage de modules (ou panneaux) photovoltaïques, eux-mêmes composés de cellules photovoltaïques nommées également photopiles.

Première partie : étude de la puissance électrique délivrée par une photopile.
Une photopile fonctionne comme un générateur réel, c’est-à-dire qu’elle peut être modélisée par une source idéale de tension placée en série avec une résistance. On la représente par le symbole de la pile avec deux flèches pointant vers le dipôle ; ces flèches symbolisent la lumière.
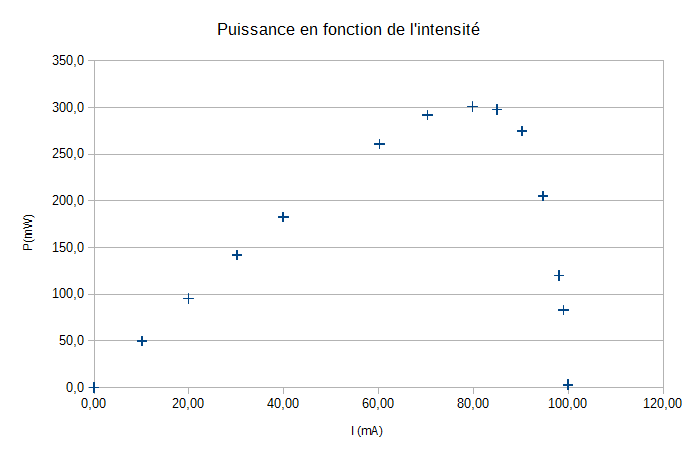
On désire tracer la courbe donnant les variations de la valeur de la puissance électrique produite par une photopile en fonction de celle de l’intensité du courant qu’elle débite.
On dispose du matériel suivant : photopile, voltmètre, ampèremètre, interrupteur (noté K), fils de connexion, boîte de résistance réglable et lampe de forte intensité.
La lampe sert à éclairer la photopile avec un éclairement constant : la puissance lumineuse qui arrive sur la photopile est toujours la même au cours de l’expérience ; elle vaut Plum = 3,0 W.
1. Quelle est la conversion d’énergie réalisée par une photopile ?
La photopile convertie de l’énergie lumineuse en énergie électrique. La photopile étant modélisée par une source idéale de tension placée en série avec une résistance, une partie de l’énergie lumineuse est convertie en énergie thermique.
Le montage expérimental nécessaire à l’étude est mis en place.
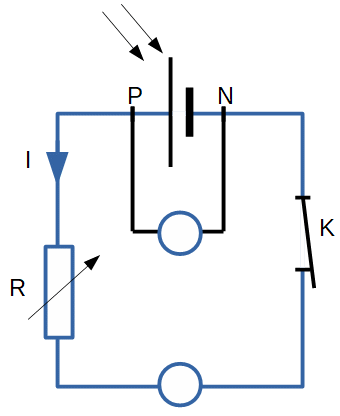
Son schéma, représenté ci-dessous, est également représenté sur l’annexe à rendre avec la copie.
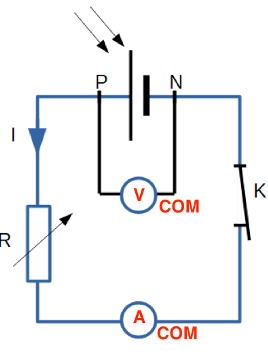
2. Compléter sur l’annexe à rendre avec la copie l’emplacement du voltmètre et de l’ampèremètre. Le symbole normalisé de l’ampèremètre est A et celui du voltmètre est V. On précisera aussi les positions des bornes « COM » de chaque appareil pour assurer la lecture d’une valeur positive.
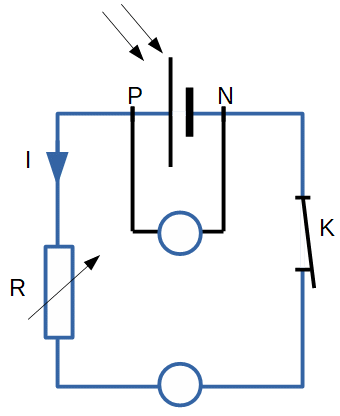
Le voltemetre se branche en dérivation et l’ampèremètre en série. La borne com est toujours placée du coté positif du générateur pour avoir une lecture positive.
3. Comment faire varier la valeur de l’intensité I du courant dans le circuit ?
En modifiant la valeur de la résistance réglable, on modifie la valeur de l’intensité dans un circuit.
$P=U\times I$
$P=50\times4,5=225\ mW$
On reporte, dans le tableau ci-dessous, les valeurs expérimentales obtenues pour les mesures de la tension électrique UPN aux bornes de la photopile et de l’intensité du courant électrique débité par la photopile. La dernière ligne du tableau fait apparaître les valeurs correspondantes (sauf une) de la puissance électrique Pél ; elles sont calculées par un tableur.
| I (mA) | 0,00 | 10,1 | 19,9 | 30,1 | 39,9 | 50,0 | 60,2 | 70,3 | 79,8 | 85,0 | 90,2 | 94,7 | 98,1 | 99,0 | 100,0 |
| UPN (V) | 4,98 | 4,92 | 4,79 | 4,72 | 4,58 | 4,50 | 4,33 | 4,15 | 3,77 | 3,51 | 3,05 | 2,16 | 1,22 | 0,84 | 0,030 |
| Pél (mW) | 0,0 | 49,7 | 95,3 | 142 | 183 | 261 | 292 | 301 | 298 | 275 | 205 | 120 | 83,0 | 3,0 |
L’évolution de la puissance électrique produite par la photopile en fonction de l’intensité du courant qu’elle débite a été tracée à partir de ces valeurs expérimentales.
Cette courbe est représentée sur l’annexe à rendre avec la copie.
Déterminer, par le calcul, la valeur manquante dans le tableau.
4. Expliquer pourquoi il n’est pas souhaitable que la photopile délivre son courant maximal.
Pour $I_{max}=100\ mA$, $P=3\ mW$. Ainsi pour le courant maximal, la valeur de la puissance est très faible.
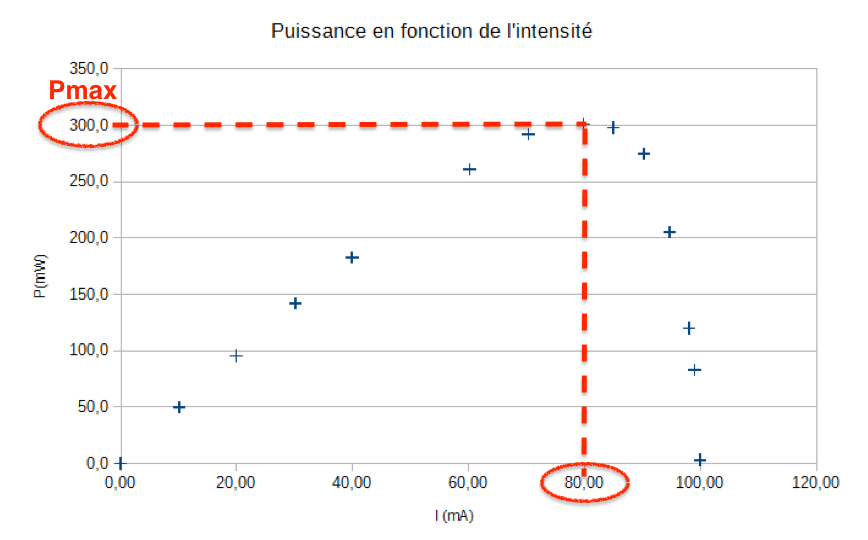
5. Pour quelle valeur de l’intensité du courant la puissance délivrée par la photopile est-elle maximale ? Que vaut alors cette puissance ? Justifier graphiquement la réponse en utilisant la courbe de l’annexe à rendre avec la copie.
Pour $I=80\ mA$, la puissance est maximale : $P_{max}=300\ mW$
6. Définir puis évaluer le rendement, noté η.
$\eta=\frac{P_{electrique}}{P_{lumineuse}}$
$\eta=\frac{300{.10}^{-3}}{3,0}=0,10=10%$
7. Formuler deux raisons pour lesquelles ce rendement n’est pas égal à 1.
Une partie de l’énergie est convertie en énergie thermique.
La photopile ne convertie pas toute l’énergie lumineuse. Seulement une partie du rayonnement reçu permet aux électrons de circuler et de créer un courant électrique.
Deuxième partie : utilisation de la photopile pour l’alimentation électrique d’un appartement.
L’éclairement en France. La puissance lumineuse reçue sur la Terre en provenance du Soleil dépend de l’endroit où l’on se trouve sur la planète, de la saison, ainsi que des conditions météorologiques. La carte ci-contre, tirée du site spécialisé en réglementation thermique et environnementale xpair.com, représente l’énergie lumineuse reçue en moyenne par unité de surface et par année en France métropolitaine :
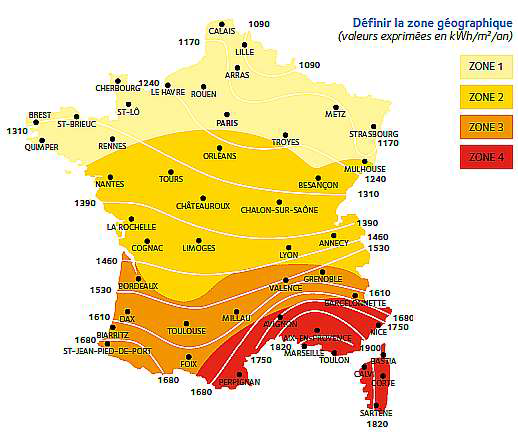
La consommation moyenne en chauffage électrique d’un appartement thermiquement bien isolé est voisine de 5.103 kWh par an.
L’étude porte sur un immeuble de 6 appartements thermiquement bien isolés, situé à Valence, dans le sud-est de la France. Sur le toit de l’immeuble est installé un dispositif de panneaux photovoltaïques recouvrant totalement une surface d’aire Spanneaux = 100 m². Ces panneaux sont confectionnés avec des photopiles identiques à celle étudiée ci-dessus ; ils fonctionnent au maximum de la puissance délivrée.
8. Quel est le nombre d’appartements de cet immeuble que cette installation de panneaux photovoltaïques permet d’alimenter en électricité ?
A Valence, l‘énergie reçue par m2 en un an est de 1530 kWh
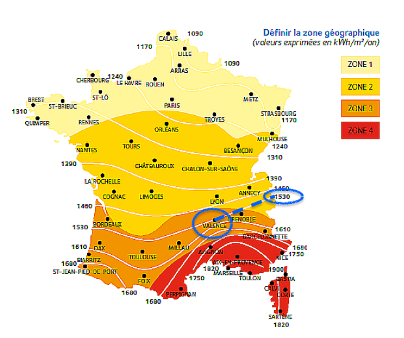
Avec une surface de 100 m2, l’énergie reçue en un an : $1530\times100=1,53{.10}^5\ kWh$
Ces panneaux solaires présentent un rendement de 10%.
L’énergie électrique :
$E_{el}=\eta\times E_{lumineuse}$
$E_{el}=0,1\times1,53{.10}^5=1,53{.10}^4\ kWh$ par an
La consommation moyenne en chauffage électrique d’un appartement thermiquement bien isolé est voisine de $5{.10}^3\ kWh$ par an :
| Energie (kWh par an) | 5.103 | $1,53{.10}^4$ |
| Nombre d’appartement | 1 | N |
$N=\frac{1\times1,53{.10}^4}{5{.10}^3}=3$
Cette installation de panneaux photovoltaïques permet d’alimenter 3 appartements.
9. utilisant les questions précédentes pour justifier vos affirmations, expliquer pourquoi le photovoltaïque contribue à faire face au réchauffement climatique, mais que cette technologie doit être associée à d’autres sources d’énergie. La réponse attendue comportera moins de dix lignes.
Ces installations utilisent l’énergie solaire (renouvelable) et permettent de pourvoir aux besoins de chauffages d’appartement (question 8). Ce ne sont donc pas des énergies fossiles qui sont utilisées pour chauffer ces appartements. Le photovoltaïque contribue donc à faire face au réchauffement climatique.
Cependant, le photovoltaïque dépend de l’ensoleillement. Ainsi dans des régions moins ensoleillées, une même surface sera moins efficace. De plus, les régions les moins ensoleillées sont celles qui ont des besoins en chauffage supérieurs.
Il faut noter également le faible rendement de ces installations.
Ainsi cette technologie doit être associée à d’autres sources d’énergie pour répondre aux enjeux énergétiques et faire face au réchauffement climatique.
Annexe à rendre avec la copie
Première partie – question 2
Première partie – question 5