Bac Centres étrangers 2023 Sujet 2
Exercice 1 – (11 points) – Durée 1h56 – Calculatrice autorisée
Sujet n°23-PYCJ2G11
Sujet et corrigé
EXERCICE 1 – PLONGEON DE HAUT VOL (11 points)
Le plongeon de haut vol est une discipline sportive qui consiste à effectuer des figures depuis une plateforme située à une vingtaine de mètres de hauteur.
Une étape du « Cliff Diving World Series » a eu lieu en 2016 à La Rochelle. Voici un extrait du journal de la région :
Le « Cliff Diving World » n’est pas seulement un spectacle aussi hallucinant que gracieux, c’est une compétition de très haut niveau avec les meilleurs athlètes mondiaux de la discipline.
Le plongeoir
Il est installé au sommet de la Tour Saint-Nicolas sur le port, à une hauteur de 27 mètres au-dessus de l’eau.
Les risques et données techniques
Le plongeon est effectué en 3 secondes. La vitesse d’impact lors de l’entrée dans l’eau est proche de 90 km/h. Le moment le plus risqué pour l’athlète est l’entrée dans l’eau. Certaines parties du corps du plongeur sont encore en pleine accélération alors que d’autres subissent une forte décélération.
D‘après un article de la Nouvelle République (avril 2017)

Dans cet exercice, on se propose d’étudier différents aspects de ce type de saut et de vérifier quelques informations de l’article. Dans chacune des parties A et B, concernant respectivement les aspects énergétiques et cinématiques du plongeur dans l’air, on se concentre sur le mouvement du centre de masse du plongeur, noté P, dans le référentiel du plongeoir supposé galiléen.
Dans tout l’exercice, la rotation du plongeur sur lui-même est négligée.
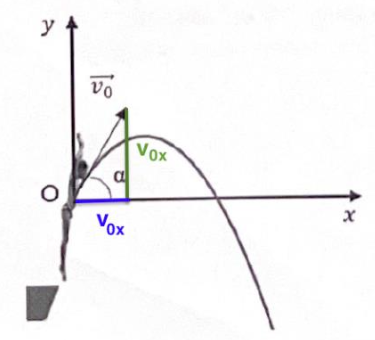
Le repère (O, x, y) est dans le plan du mouvement. Son origine O coïncide avec la position du centre de masse P du plongeur à l’instant t = 0 s (figure 1).
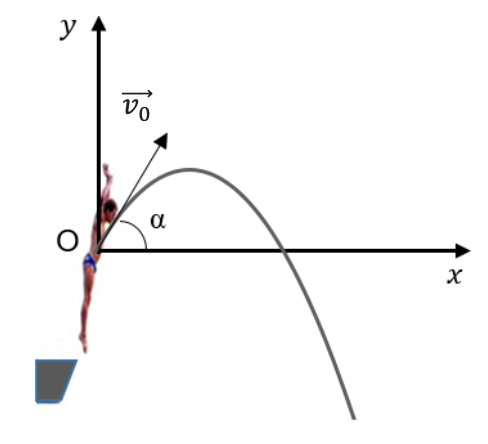
Lors du saut, le plongeur se propulse et acquiert ainsi une vitesse initiale à la date t = 0 caractérisée par le vecteur vitesse initiale $\overrightarrow{v_0}$ incliné d’un angle 𝛼 avec l’horizontale.
Une chronophotographie a permis d’obtenir les valeurs des coordonnées du centre de masse P du plongeur au cours du temps.
Sur la figure 1 ci-dessous, on donne le schéma de principe de la situation, l’allure de la trajectoire de P ainsi que les valeurs des coordonnées de P pour les cinq premiers points.
| 𝑡 (s) | 𝑥 (m) | 𝑦 (m) |
| 0 | 0 | 0 |
| 0,033 | 0,050 | 0,060 |
| 0,067 | 0,10 | 0,11 |
| 0,100 | 0,15 | 0,15 |
| 0,133 | 0,21 | 0,18 |
Figure 1- Schéma et coordonnées du centre de masse P du plongeur
Données
- Masse du plongeur 𝑚 = 70,0 kg
- Intensité de la pesanteur 𝑔 = 9,81 m ∙ s−2
Partie A – Étude énergétique
Pour effectuer l’étude énergétique, on utilise un programme Python dont un extrait est reproduit figure 2 ci-dessous.
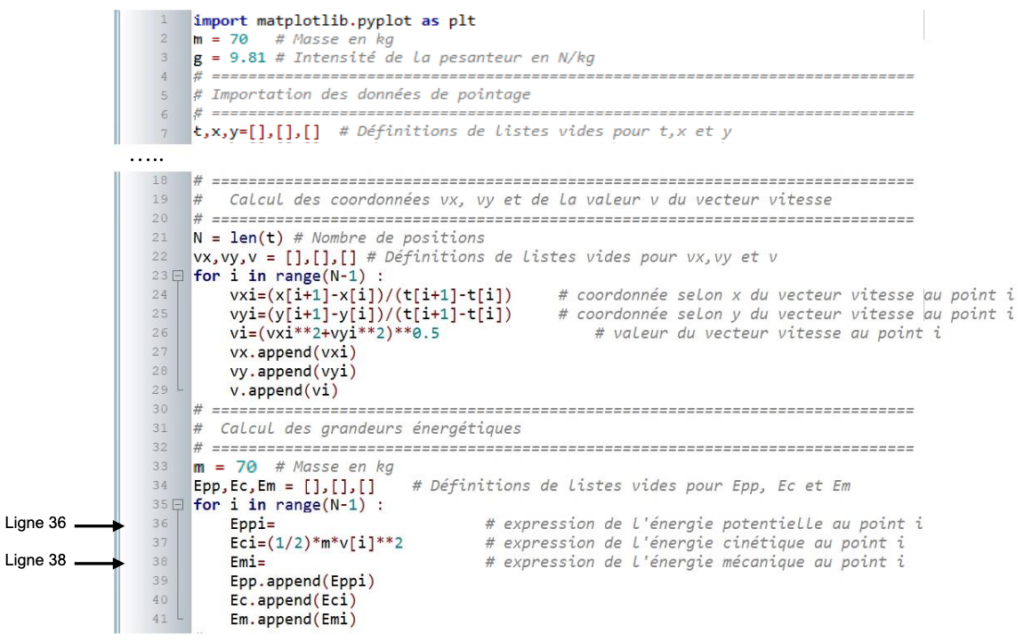
Figure 2 – Extrait du code Python
Grâce au programme Python, on peut calculer les valeurs des énergies potentielle de pesanteur (Epp), cinétique (Ec) et mécanique (Em) du plongeur.
L’énergie potentielle de pesanteur est prise nulle pour 𝑦 = 0 m.
1. Recopier et compléter les instructions des lignes 36 et 38 du programme Python.
Ligne 36 : Eppi=m*g*y[i]
Ligne 38 : Emi= Eci+ Eppi
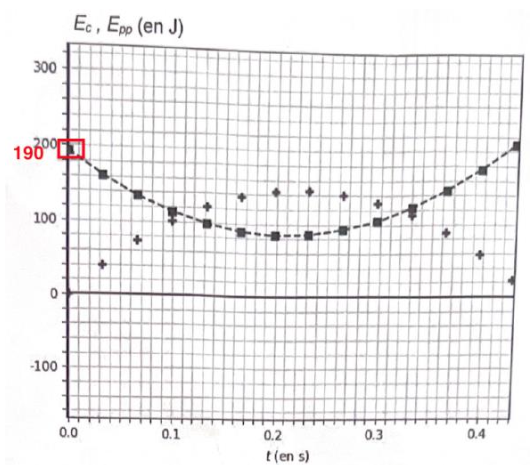
Le programme permet d’obtenir des représentations graphiques des évolutions au cours du temps des énergies cinétique et potentielle du plongeur durant les quelques millisecondes qui suivent le début de sa chute (voir figure 3 ci-après).
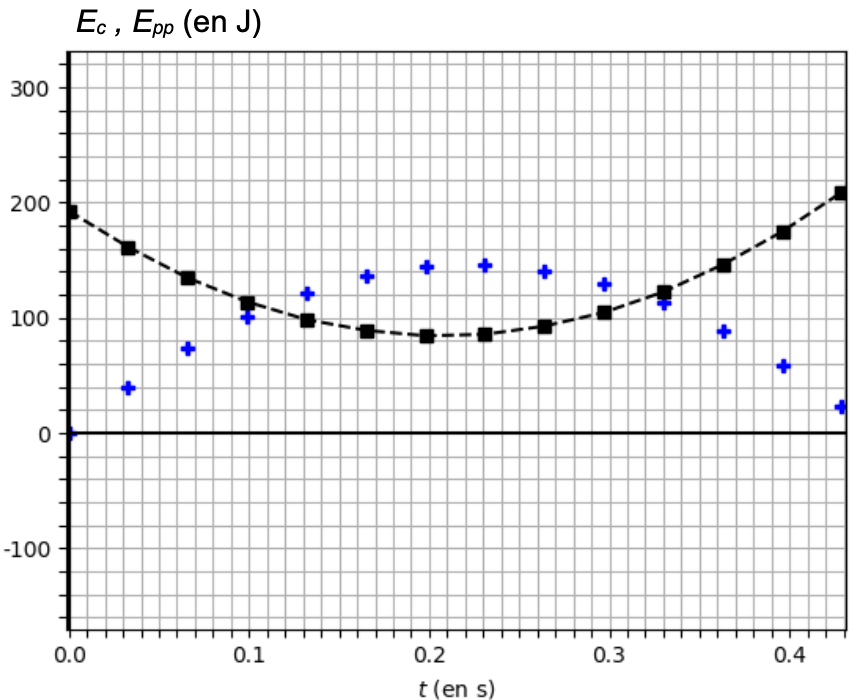
Figure 3 – Évolution des énergies cinétique et potentielle au tout début du saut
2. Justifier que la courbe en pointillés sur la figure 3 ci-dessus est celle de l’évolution de l’énergie cinétique au cours du temps.
V0 n’est pas nul, ainsi l’énergie cinétique initiale n’est pas nulle.
La figure 3 est l’évolution au cours du temps de l’énergie cinétique et de l’énergie potentielle.
Seule la courbe en pointillés n’est pas nulle pour t=0 : la courbe en pointillés est celle de l’évolution de l’énergie cinétique.
3. Montrer, à partir de la courbe de l’énergie cinétique, que la valeur de la vitesse initiale est de l’ordre de 𝑣0 = 2,3 m · s−1.
$$
{\rm E}{c_0}=\frac{1}{2}\times m \times v_0^2
$$
$$
\frac{1}{2}\times m \times v_0^2={\rm E}{c_0}
$$
$$
v_0^2=\frac{2{\rm E}{c_0}}{m}
$$
$$
v_0=\sqrt{\frac{2{\rm E}{c_0}}{m}}
$$
$$
v_0=\sqrt{\frac{2\times190}{70,0}}
$$
$$
v_0=2,3\ m.s^{-1}
$$
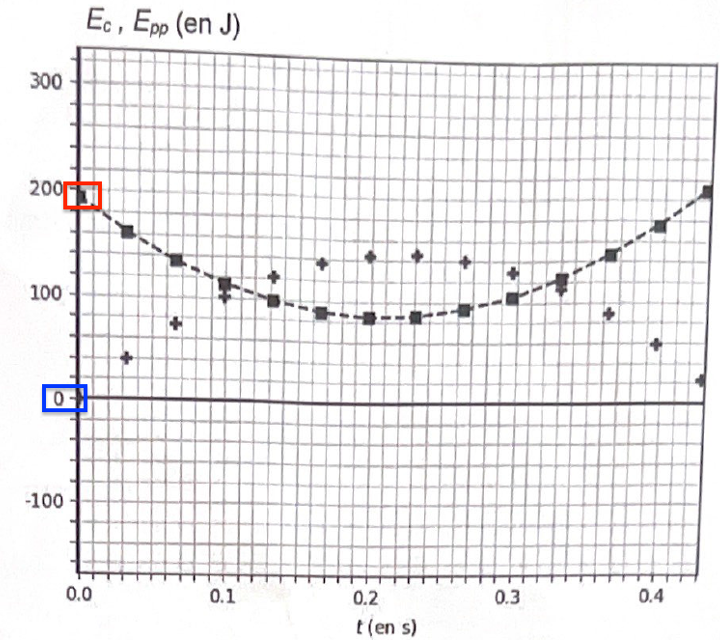
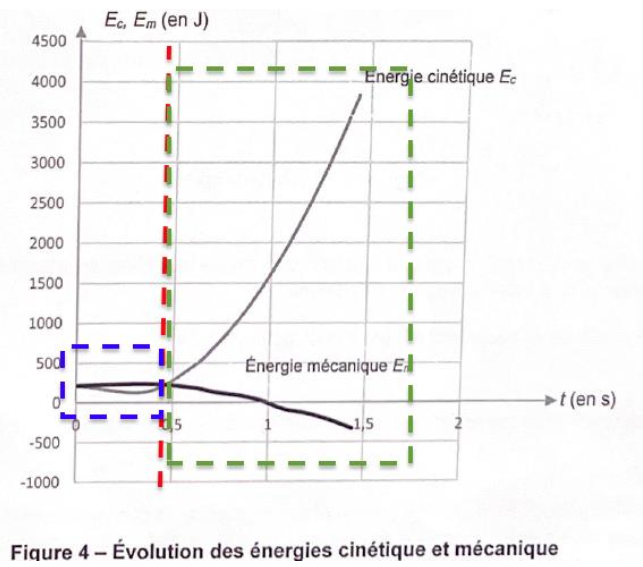
Un autre relevé des coordonnées du point P, effectué sur une durée plus longue, conduit aux tracés figure 4 ci-dessous.
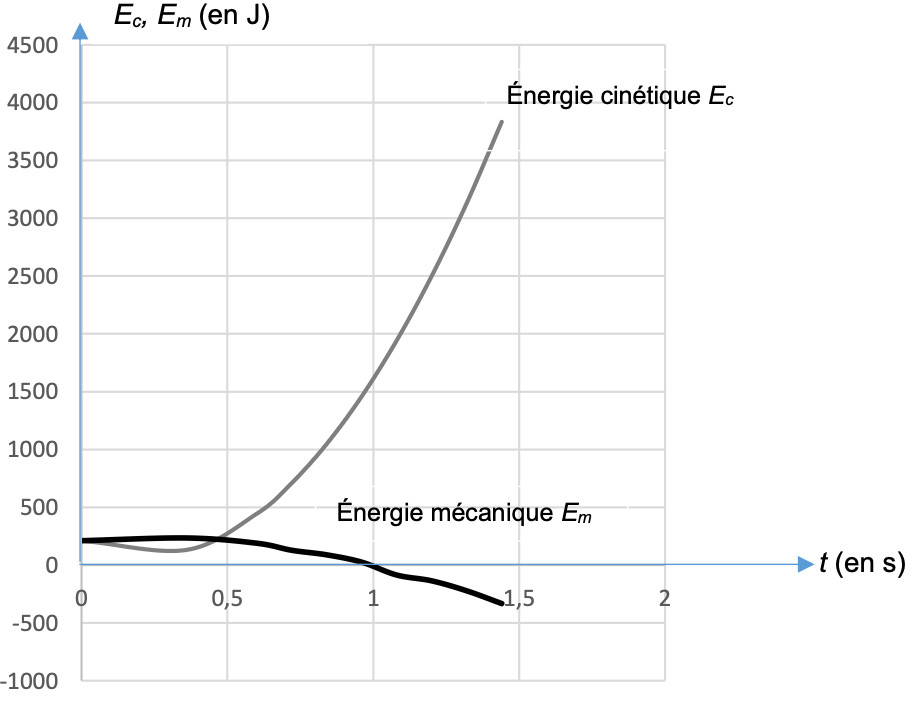
Figure 4 – Évolution des énergies cinétique et mécanique
On constate que l’énergie mécanique reste constante si 𝑡 ≤ 0,4 s, puis décroit progressivement.
4. Pour chacune des deux phases, 𝑡 ≤ 0,4 s puis 𝑡 ˃ 0,4 s, préciser si les frottements sont négligeables ou non. Justifier.
Lorsque l’énergie mécanique est constante, les forces de frottements sont négligeables.
Ainsi :
Pour $t\le0,4\ s$ l’énergie mécanique est constante, les forces de frottements sont négligeables.
Pour $t>0,4\ s$ l’énergie mécanique décroit, les forces de frottements ne sont pas négligeables.
5. En observant les courbes sur la figure 4, formuler une hypothèse sur l’importance des forces de frottement en fonction de la valeur de la vitesse, suivant que celle-ci est faible ou élevée.
En observant les courbes de la figure 4, on remarque que :
- pour une énergie cinétique faible l’énergie mécanique reste constante.
- pour une énergie cinétique élevée l’énergie mécanique diminue.
On peut emmètre l’hypothèse que :
- pour des vitesses élevées, les forces de frottements ne sont pas négligeables.
- pour des vitesses faibles, les forces de frottements sont négligeables.
Partie B – Étude cinématique
Dans cette partie, à l’aide des lois de la mécanique, on cherche à retrouver la forme de la trajectoire observée ainsi que les valeurs de la durée de chute dans l’air et de la vitesse lors de l’entrée dans l’eau.
6. En utilisant des valeurs du tableau de données (figure 1), calculer les valeurs de 𝑣0𝑥 et 𝑣0𝑦, coordonnées du vecteur vitesse initiale $\overrightarrow{v_0}$ à la date t = 0 s, en appliquant les instructions des lignes 24 et 25 du code Python (figure 2).
Ligne 24 : vxi=(x[i+1]-x[i])/(t[i+1]-t[i])
Ligne 25 : vyi=(y[i+1]-y[i])/(t[i+1]-t[i])
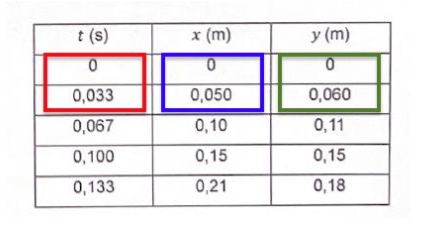
v0x=vx0=(x[0+1]-x[0])/(t[0+1]-t[0])
v0x= (0,050-0)/(0,033-0)
v0x= 1,5 m.s-1
v0y=vy0=(y[0+1]-y[0])/(t[0+1]-t[0])
v0y= (0,060-0)/(0,033-0)
v0y= 1,8 m.s-1
7. À partir des valeurs de 𝑣0𝑥 et 𝑣0𝑦, vérifier que la valeur de l’angle 𝛼 est de l’ordre de 𝛼 = 50°.
$$
\cos(\alpha)=\frac{v_{0x}}{v_0}
$$
$$
\cos(\alpha)=\frac{1,5}{2,3}
$$
$$
\cos(\alpha)=0,65
$$
$$
\alpha=\text{Arccos}(0,65)=49,5°
$$
$$
\sin(\alpha)=\frac{v_{0y}}{v_0}
$$
$$
\sin(\alpha)=\frac{1,8}{2,3}
$$
$$
\sin(\alpha)=0,78
$$
$$
\alpha=\text{Arcsin}(0,78)=51,3°
$$
L’angle $\alpha$ est de l’ordre de $\alpha=50°$.
Pour la suite de cette partie B, on néglige les actions exercées par l’air sur le plongeur et on fait l’hypothèse de la chute libre, ce qui revient à considérer que la seule force extérieure subie par le plongeur est son poids. On utilise ainsi un modèle simplifié permettant de déterminer les valeurs de différentes grandeurs puis de les comparer avec les résultats expérimentaux et les indications de l’article.
À 𝑡 = 0 s, le centre de masse P du plongeur est en O, à 28 m au-dessus du niveau de l’eau.
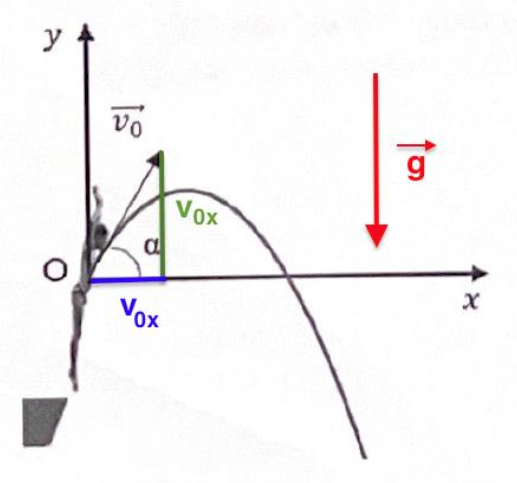
8. Écrire la relation traduisant l’application de la deuxième loi de Newton sur le plongeur de masse 𝑚 en utilisant les grandeurs $\overrightarrow{g}$, champ de pesanteur, et $\overrightarrow{a}$, accélération du centre de masse du plongeur.
Système : plongeur
Référentiel terrestre supposé galiléen.
D’après la deuxième loi de newton :
$$
\Sigma \overrightarrow{F_{ext}}=m\overrightarrow{a}
$$
$$
\overrightarrow{P}=m\overrightarrow{a}
$$
$$
m\overrightarrow{g}=m\overrightarrow{a}
$$
$$
\overrightarrow{g}=\overrightarrow{a}
$$
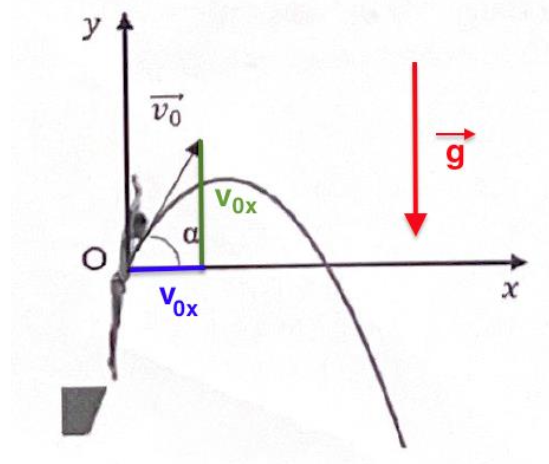
9. Exprimer littéralement les coordonnées 𝑎𝑥(𝑡) et 𝑎𝑦(𝑡) du vecteur accélération $\overrightarrow{a}(t)$, ainsi que les coordonnées 𝑣𝑥(𝑡) et 𝑣𝑦(𝑡) du vecteur vitesse $\overrightarrow{v}(t)$, en fonction de 𝑣0, 𝑔, 𝑡 et 𝛼.
$$
\overrightarrow{g}=\overrightarrow{a}
$$
$$
\overrightarrow{g}\begin{cases}
0\\
-g
\end{cases}
$$
Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.
$$
\overrightarrow{a}\begin{cases}
a_x(t)=0\\
a_y(t)=-g
\end{cases}
$$
$$
\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}
$$
$$
\overrightarrow{v}\begin{cases}
v_x(t)=C_1\\
v_y(t)=-g t+C_2
\end{cases}
$$
Pour trouver les constantes, on utilise $\overrightarrow{v_0}$
$$
\overrightarrow{v_0}\begin{cases}
v_{0x}=v_0 \cos\alpha\\
v_{0y}=v_0 \sin\alpha
\end{cases}
$$
d’ou
$$
\overrightarrow{v}\begin{cases}
v_x(t)=v_0 \cos\alpha\\
v_y(t)=-g t+v_0 \sin\alpha
\end{cases}
$$
10. Montrer que les équations horaires du mouvement du centre de masse du plongeur ont pour expression :
$$\overrightarrow{OP}(t)\begin{cases}
x(t)=v_0 \times \cos(\alpha) \times t \\
y(t)=-\dfrac{1}{2} \times g \times t^2+v_0 \times \sin(\alpha) \times t
\end{cases}$$
$$
\overrightarrow{v}=\frac{d\overrightarrow{OM}}{dt}
$$
$$
\overrightarrow{OP}(t)\begin{cases}
x(t)=v_0 \times \cos(\alpha) \times t + C_3\\
y(t)=-\frac{1}{2}\times g \times t^2+v_0 \times \sin(\alpha) \times t + C_4
\end{cases}
$$
Pour trouver les constantes, on utilise $\overrightarrow{OM}_0$
$$
\overrightarrow{OP}(0)\begin{cases}
x_0=0v
y_0=0
\end{cases}
$$
d’ou
$$
\overrightarrow{OP}(t)\begin{cases}
x(t)=v_0 \times \cos(\alpha) \times t\\
y(t)=-\frac{1}{2}\times g \times t^2+v_0 \times \sin(\alpha) \times t
\end{cases}
$$
11. Établir l’équation de la trajectoire et montrer qu’elle est compatible avec l’allure de la trajectoire représentée sur la figure 1.
On isole t :
$$
x=v_0 \cos(\alpha) \times t
$$
$$
v_0 \cos(\alpha) \times t=x
$$
$$
t=\frac{x}{v_0 \cos(\alpha)}
$$
On remplace t dans y :
$$
y(t)=-\frac{1}{2} g t^2+v_0 \sin(\alpha) \times t
$$
$$
y(x)=-\frac{1}{2} g \left(\frac{x}{v_0 \cos(\alpha)}\right)^2+v_0 \sin(\alpha) \times \frac{x}{v_0 \cos(\alpha)}
$$
$$
y(x)=-\frac{1}{2} g \frac{x^2}{v_0^2 \cos^2(\alpha)}+x \times \tan(\alpha)
$$
$y=f(x)$ est de la forme $a x^2+b x$ : la courbe $y=f(x)$ est une parabole. Elle est compatible avec l’allure de la trajectoire représentée figure 1.
12. À partir des équations horaires, montrer que la durée de la chute peut être obtenue en résolvant l’équation du second degré :
−4,9 𝑡2 + 1,8 𝑡 + 28 = 0 (équation 1)
$$
y(t)=-\frac{1}{2}\times g \times t^2+v_0 \times \sin(\alpha) \times t
$$
La durée de chute est obtenue lorsque le plongeur touche l’eau soit pour $y=-28 m$
$$
-28=-\frac{1}{2}\times g \times t^2+v_0 \times \sin(\alpha) \times t
$$
$$
-28=-\frac{1}{2}\times 9,8 \times t^2+2,3 \times \sin(50) \times t
$$
$$
0=-4,9 t^2+1,8 \times t+28
$$
$$
-4,9 t^2+1,8 \times t+28=0
$$
Mathématiquement, l’équation 1 admet deux solutions que l’on peut écrire :
𝑡1 = −2,21 s et 𝑡2 = 2,58 s
Expérimentalement, la durée de la chute mesurée est : ∆𝑡𝑒𝑥𝑝 = 2,8 s. La valeur de l’incertitude sur cette durée mesurée est 𝑢(∆𝑡𝑒𝑥𝑝) = 0,3 s.
13. Vérifier que l’hypothèse de la chute libre, posée pour établir les équations horaires, conduit à une valeur de la durée de chute en accord avec le résultat expérimental.
Pour la valeur du temps, on ne retient que la valeur positive soit $\mathbf{t}_2=2,58\ s$
Calculons le Z-score :
$$
z=\frac{|x-x_{ref}|}{u(x)}
$$
$$
z=\frac{\Delta t_{exp}-t_2}{u(\Delta t_{exp})}
$$
$$
z=\frac{|2,8-2,58|}{0,3}
$$
$$
z=0,73
$$
$z<2$, $\Delta t_{exp}$ et $t_2$ sont compatibles.
Ainsi, l’hypothèse de la chute libre conduit à une valeur de la durée de chute en accords avec le résultat expérimental.
14. Montrer que la valeur de la vitesse lors de l’entrée dans l’eau 𝑣𝑡ℎ prédite par l’étude cinématique est de l’ordre de 24 m·s-1.
$$
\overrightarrow{v}_{th}=\overrightarrow{v}(t_2)\begin{cases}
v_x(t_2)=v_0 \cos\alpha\\
v_y(t_2)=-g t_2+v_0 \sin\alpha
\end{cases}
$$
$$
v_{th}=v(t_2)=\sqrt{\left(v_x(t_2)\right)^2+\left(v_y(t_2)\right)^2}
$$
$$
v_{th}=\sqrt{\left(v_0 \cos\alpha\right)^2+\left(-g t_2+v_0 \sin\alpha\right)^2}
$$
$$
v_{th}=\sqrt{\left(2,3 \times \cos(50)\right)^2+\left(-9,8 \times 2,58+2,3 \times \sin(50)\right)^2}
$$
$$
v_{th}=24\ m.s^{-1}
$$
15. Indiquer si la valeur 𝑣𝑡ℎ obtenue à la question 14 est en accord ou non avec la valeur citée dans l’article introductif.
Le texte introductif donne une valeur de vitesse d’impact lors de l’entrée dans l’eau proche de $90\ km.h^{-1}$
$$
\frac{90}{3,6}=25\ m.s^{-1}
$$
$v_{th}=24\ m.s^{-1}$ est donc en accord avec la valeur citée dans l’article introductif.
Une fois dans l’eau, le plongeur s’immobilise en 0,5 s.
16. Donner une estimation de la valeur de l’accélération 𝑎𝑒𝑎𝑢 subie par le plongeur une fois dans l’eau en s’appuyant sur la valeur de la vitesse obtenue à la question 14. Comparer ce résultat à l’intensité du champ de pesanteur g.
$$
a_y=\frac{\Delta v}{\Delta t}
$$
$$
a_y=\frac{v_f-v_{th}}{\Delta t}
$$
$$
a_y=\frac{0-24}{0,5}
$$
$$
a_y=-48\ m.s^{-2}
$$
L’accélération est négative car dirigée vers le bas.
$$
a=\sqrt{\left(a_x\right)^2+\left(a_y\right)^2}
$$
$$
a=\sqrt{\left(0\right)^2+\left(-48\right)^2}
$$
$$
a=48\ m.s^{-2}
$$
Comparons ce résultat à l’intensité du champ de pesanteur $g$ :
$$
\frac{a}{g}=\frac{48}{9,81}=4,9
$$
L’accélération est près de 5 fois supérieure à l’accélération de pesanteur $g$.
