Population de la France métropolitaine de 1946 à 2050

Enseignement scientifique Terminale

Durée 1h – 10 points – Thème « Une histoire du vivant »

Le tableau ci-dessous donne l’évolution de la population en France métropolitaine de 1946 à 2013.

Année	1946	1954	1962	1968	1975	1982	1990	1999	2006	2013
Rang xi	0	8	16	22	29	36	44	53	60	67
Population en millions yi	40,5	42,8	46,5	49,8	52,7	54,3	56 ,6	58,2	61,4	63,7

Afin de faire des prévisions, cette évolution est représentée par un nuage de points dans le but d’en faire un ajustement affine.

Une équation de la droite d’ajustement du nuage est : y = 0,341x + 41,21.

1- Parmi les trois graphiques ci-dessous, quel est selon vous celui qui correspond à la droite d’ajustement trouvée ? Justifier.

Une équation de la droite d’ajustement du nuage est : y = 0,341x + 41,21.

C’est une droite (on élimine le graphique 2) qui passe au plus près du nuage de points (on élimine le graphique 3).

Parmi les trois graphiques celui qui correspond à la droite d’ajustement trouvée est le graphique 1.

2- Après avoir déterminé le rang correspondant à l’année 2020, montrer, à l’aide de l’équation de la droite, que le modèle prévoit une population française de 66,4 millions d’habitants à cette date.

Année	1946	1954	1962	1968	1975	1982	1990	1999	2006	2013
Rang xi	0	8	16	22	29	36	44	53	60	67

Le rang 0 correspond l’année 1946.

Le rang 8 correspond à l’année 1954 car 1954-1946=8

Le rang 16 correspond à l’année 1962 car 1962-1946=16

Etc.

Rang correspondant à l’année 2020 :

2020-1946=74

Population française prévu à l’aide de l’équation de la droite à cette date.

y = 0,341x + 41,21

y = 0,341×74+ 41,21

y = 66,4

Le modèle prévoit une population française de 66,4 millions d’habitants à l’année 2020.

Le recensement effectué au cours de l’année 2020 montre que la population en France métropolitaine est de 64,9 millions d’habitants.

3- Au-delà d’un écart supérieur à un million, ce modèle n’est pas valide. Conclure sur la validité du modèle en 2020. Justifier la réponse.

Le recensement effectué au cours de l’année 2020 montre que la population en France métropolitaine est de 64,9 millions d’habitants.

Calculons l’écart avec ce modèle :

66,4-64,9=1,5 millions

L’écart supérieur à un million donc ce modèle n’est pas valide.

Afin d’affiner les prévisions, il est envisagé de modifier le modèle précédent. Les relevés annuels de la population en France Métropolitaine de 2013 à 2020 sont donnés ci-dessous :

Année	2013	2014	2015	2016	2017	2018	2019	2020
Rang xi	0	1	2	3	4	5	6	7
Population en millions yi	63,7	64	64,3	64,5	64,6	64,7	64,8	64,9

Une droite d’équation y = 0,163x + 63,87 correspond au nouveau modèle choisi pour les 30 années à venir.

Nous souhaitons savoir à partir de quelle année la population en France métropolitaine dépassera, d’après le nouveau modèle, les 65,5 millions d’habitants.

Afin d’automatiser les calculs, nous avons programmé la fonction seuil_pop en langage Python ci-contre.

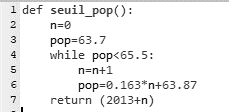
4- Recopier parmi les quatre propositions suivantes celle qui correspond à la donnée manquante du programme :

            Proposition a : pop = 0.163*n+0

            Proposition b : pop = 0.163*n+63.87

            Proposition c : pop = pop+1

            Proposition d : pop = 0.163*pop+63.87

D’après l’énoncé : « Une droite d’équation y = 0,163x + 63,87 correspond au nouveau modèle choisi pour les 30 années à venir. »

Parmi les quatre propositions suivantes celle qui correspond à la donnée manquante du programme est la Proposition b : pop = 0.163*n+63.87

5- À partir de quelle année la population en France métropolitaine dépassera-t-elle les 65,5 millions d’habitants ?

y = 0,163x + 63,87

Trouvons à partir de quelle année la population en France métropolitaine dépassera-t-elle les 65,5 millions d’habitants :

0,163x + 63,87>65,5

0,163x >65,5- 63,87

0,163x >1,63

x>1,63/(0,163 )

x>10

soit 10 ans après l’année 2013 : 10+2013=2023 La population en France métropolitaine dépassera les 65,5 millions d’habitants à partir de l’année 2023.