Protection des crapauds

Bac Métropole mars 2023 Sujet 2

Exercice 2 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°23-PYCJ2ME1

Sujet et corrigé

EXERCICE 2 – PROTECTION DES CRAPAUDS (5 points)

Barrière de protection le long d’une route

Pour éviter qu’ils ne se fassent écraser en passant sur la route qui traverse cette zone de migration, un dispositif a été installé : des barrières en bois, suffisamment hautes pour empêcher le saut sur la route, sont placées de chaque côté, obligeant les amphibiens à emprunter des passages souterrains appelés « crapauducs ».

Dans cet exercice, on se propose d’étudier le mouvement lors d’un saut d’un crapaud Bufo bufo de façon à déterminer la hauteur minimale des barrières de protection le long d’une route.

Le système considéré est un crapaud dont on étudie le mouvement du centre de masse, noté G. Le champ de pesanteur terrestre local $\overrightarrow{g}$ est considéré uniforme et les frottements liés à l’action de l’air sont supposés négligeables face au poids.

Données :

• intensité de la pesanteur terrestre : g = 9,81 m·s^-2 ;
• taille moyenne d’un crapaud Bufo bufo : 10 cm.

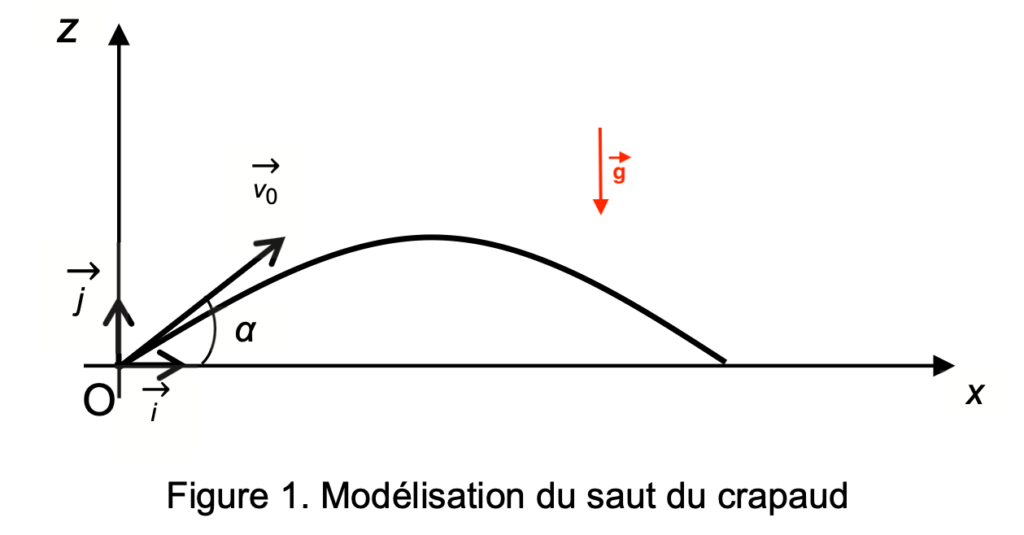
Le mouvement du centre de masse G du crapaud est étudié dans le référentiel terrestre supposé galiléen et muni du système d’axes (Ox, Oz), respectivement horizontal muni du vecteur unitaire $\overrightarrow{i}$ et vertical muni du vecteur unitaire $\overrightarrow{j}$ (voir figure 1).

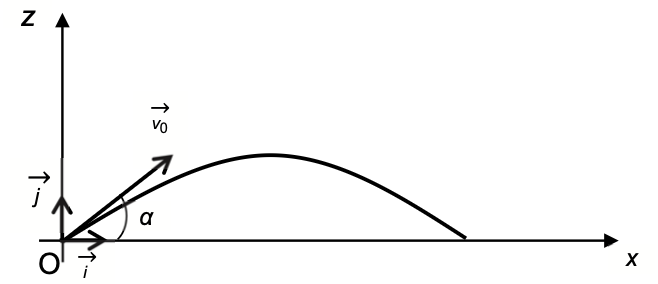
Figure 1. Modélisation du saut du crapaud

À la date t = 0 s, le centre de masse G est placé à l’origine du repère O et son vecteur vitesse initiale, noté

$\overrightarrow{v_0}$, a une direction faisant un angle αavec l’axe horizontal (Ox). On note v₀ la norme de $\overrightarrow{v_0}$.

Q1. Établir les expressions littérales des composantes ax et a_z du vecteur accélération $\overrightarrow{a_G}$ du centre de masse du crapaud suivant les axes Ox et Oz.

Système : crapaud
Référentiel terrestre supposé galiléen.

D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a_G}$$
$$\overrightarrow{P}=m\overrightarrow{a_G}$$
$$m\overrightarrow{g}=m\overrightarrow{a_G}$$
$$\overrightarrow{g}=\overrightarrow{a_G}$$

$$\overrightarrow{a_G}=\overrightarrow{g}$$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.

$$\overrightarrow{a_G}\begin{cases}a_{x(t)}=0 \\ {a}_{z\left(t\right)}=-g\end{cases}$$

Q2. Établir les expressions littérales des composantes v_x(t) et v_z(t) du vecteur vitesse $\overrightarrow{v_G}$ du centre de masse du crapaud suivant les axes Ox et Oz.

$$\overrightarrow{a_G}=\frac{d\overrightarrow{v_G}}{dt}$$

On intègre le système d’équation précédent :
$$\overrightarrow{v_G}\begin{cases}v_{x(t)}=C_1 \\ {v}_{z\left(t\right)}=-gt+C_2\end{cases}$$

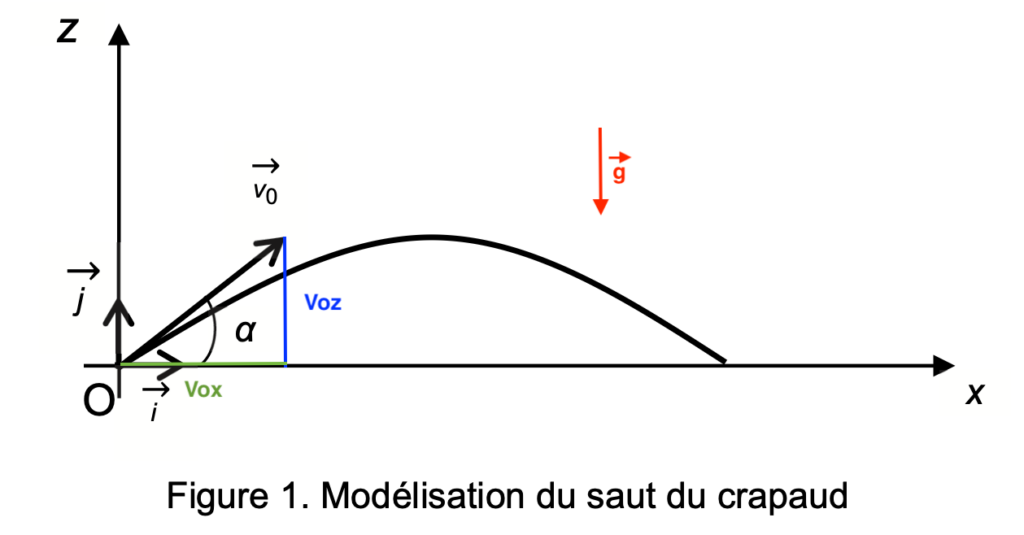
d’ou

$$\overrightarrow{v_G}\begin{cases}v_{x(t)}=v_0\ \cos\alpha \\ {v}_{z\left(t\right)}=-gt+v_0\ \sin\ \alpha\end{cases}$$

Q3. Montrer que les expressions littérales des équations horaires x(t) et z(t) de la position du centre de masse G du crapaud au cours de son mouvement s’écrivent :

$$\begin{cases}
x(t)=v_0\cdot\cos(\alpha)\cdot t\\
z(t)=-\dfrac{1}{2}\cdot g\cdot t^2+v_0\cdot\sin(\alpha)\cdot t
\end{cases}$$

$$\overrightarrow{v_G}=\frac{d\overrightarrow{OG}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{OG}(t)\begin{cases}x\left(t\right)=\ v_0\times \cos\left(\alpha\right)\times t\ +C_3 \\ z\left(t\right)=-\frac{1}{2}\times g\times t^2+v_0\times \sin\left(\alpha\right)\times t\ +C_4\end{cases}$$

Pour trouver les constantes, on utilise ${\overrightarrow{OG}}_0$

$$\overrightarrow{OG}(0)\begin{cases}x_0=0 \\ z_0=0\end{cases}$$

d’ou
$$\overrightarrow{OG}(t)\begin{cases}x\left(t\right)=v_0\times \cos{\left(\alpha\right)}\times t \\ z\left(t\right)=-\frac{1}{2}\times g\times t^2+v_0\times \sin{\left(\alpha\right)}\times t\end{cases}$$

Q4. Établir l’expression de la durée du saut du crapaud, notée t_saut, en fonction de v₀, g, et α.

La durée du saut du crapaud correspond au temps pour lequel le crapaud retombe au sol : $$z(t_{saut})=0$$
$$z\left(t\right)=-\frac{1}{2}\times g\times t^2+v_0\times \sin{\left(\alpha\right)}\times t$$
$$z\left(t_{saut}\right)=-\frac{1}{2}\times g\times{t_{saut}}^2+v_0\times \sin{\left(\alpha\right)}\times t_{saut}$$
$$0=t_{saut}\times\left(-\frac{1}{2}\times g\times t_{saut}+v_0\times \sin{\left(\alpha\right)}\right)$$

Un produit de facteur est nul si et seulement si un des facteurs est nul :
$t_{saut}=0$ : valeur du temps correspondant au début du saut, solution qu’on ne gardera donc pas.
$$-\frac{1}{2}\times g\times t_{saut}+v_0\times \sin{\left(\alpha\right)}=0$$
$$-\frac{1}{2}\times g\times t_{saut}=-v_0\times \sin{\left(\alpha\right)}$$
$$\frac{1}{2}\times g\times t_{saut}=v_0\times \sin{\left(\alpha\right)}$$
$$t_{saut}=\frac{2\times v_0\times \sin{\left(\alpha\right)}}{g}$$

Q5. En utilisant l’expression de x(t) et l’expression de t_saut obtenue à la réponse à la question Q4, montrer que la vitesse v₀ permettant au crapaud d’effectuer un saut de longueur d est donnée par la relation :

$$v_0=\sqrt{\dfrac{g\cdot d}{2\cdot\sin(\alpha)\cdot\cos(\alpha)}}$$

$$x\left(t\right)=v_0\times \cos{\left(\alpha\right)}\times t$$
Pour $t_{saut}$ : $x\left(t_{saut}\ \right)=d$
$$t_{saut}=\frac{2\times v_0\times \sin{\left(\alpha\right)}}{g}$$

$$x\left(t_{saut}\ \right)=v_0\times \cos{\left(\alpha\right)}\times t_{saut}$$
$$d=v_0\times \cos{\left(\alpha\right)}\times\frac{2\times v_0\times \sin{\left(\alpha\right)}}{g}$$
$$d=\frac{2\times{v_0}^2\times \cos{\left(\alpha\right)}\times \sin{\left(\alpha\right)}}{g}$$
$$\frac{2\times{v_0}^2\times \cos{\left(\alpha\right)}\times \sin{\left(\alpha\right)}}{g}=d$$
$${v_0}^2=\frac{d\times g}{2\times \cos{\left(\alpha\right)}\times \sin{\left(\alpha\right)}}$$
$$v_0=\sqrt{\frac{g\times d}{2\sin{\left(\alpha\right)}\times \cos{\left(\alpha\right)}}}$$

Q6. Sachant que les crapauds les plus puissants peuvent faire des sauts d’une longueur égale à 20 fois leur taille, calculer la valeur de v₀ qu’ils atteignent pour un angle α = 45°.

Saut d’une longueur de 20 fois leur taille :$$\ d=20\times10{\times10}^{-2}=2\ m$$

$$v_0=\sqrt{\frac{9,81\times2}{2\sin{\left(45\right)}\times\cos{\left(45\right)}}}$$
$$v_0=4,4\ m.s^{-1}$$

La hauteur maximale z_max d’un saut est obtenue lorsque ce saut est vertical ; l’angle α vaut alors α = 90°, la vitesse initiale est toujours notée v₀.

Q7. Établir que la hauteur maximale d’un saut a pour expression littérale :

$$z_{\max}=\dfrac{v_0^2}{2\cdot g}$$

Méthode 1 : avec les équations horaires
$z_{max}$ pour $\alpha=90°$
De plus, l’altitude est maximale lorsque ${\ v}{z\left(t{max}\right)}=0$ (le crapaud ne monte plus) :
$${\ v}{z\left(t\right)}=-gt+v_0\ \sin\ \alpha$$
$${\ v}{z\left(t_{max}\right)}=-gt_{max}+v_0\ \sin\ 90°$$
$$0=-gt_{max}+v_0$$
$$gt_{max}=v_0$$
$$t_{max}=\frac{v_0}{g}$$

Or
$$z\left(t\right)=-\frac{1}{2}\times g\times t^2+v_0\times \sin{\left(\alpha\right)}\times t$$
$$z_{max}=-\frac{1}{2}\times g\times t_{\max}^2+v_0\times \sin{\left(90\right)}\times t_{max}$$
$$z_{max}=-\frac{1}{2}\times g\times\left(\frac{v_0}{g}\right)^2+v_0\times \sin{\left(90\right)}\times\frac{v_0}{g}$$
$$z_{max}=-\frac{1}{2}\times g\times\frac{v_0^2}{g^2}+v_0\times\frac{v_0}{g}$$
$$z_{max}=-\frac{1}{2}\times\frac{v_0^2}{g}+\frac{v_0^2}{g}$$
$$z_{max}=\frac{1}{2}\times\frac{v_0^2}{g}$$
$$z_{max}=\frac{v_0^2}{2g}$$

 
Méthode 2 : avec le théorème de l’énergie cinétique
$$\Delta E_C=\Sigma W_{AB}(\overrightarrow{F})$$
$$E_{C\ finale}-E_{C\ initiale}=W_{AB}(\overrightarrow{P})$$
$$\frac{1}{2}m.v_{finale}^2-\frac{1}{2}m.v_0^2=m\times g\times\left(z_0-z_{max}\right)$$
Avec ${\ v}{finale}=0$ (le crapaud ne monte plus) et $z_0=0$
$$0-\frac{1}{2}m.v_0^2=m\times g\times\left(0-z{max}\right)$$
$$-\frac{1}{2}m.v_0^2=-m\times g\times z_{max}$$
$$z_{max}=\frac{1}{2}\frac{m.v_0^2}{m\times g}$$
$$z_{max}=\frac{v_0^2}{2g}$$

Méthode 3 : Loi de conservation de l’énergie mécanique : nous sommes en chute libre, il n’y a pas de frottements, l’énergie mécanique se conserve.
$$E_{m(B)}=E_{m(0)}$$
$$E_{C\ (B)}+E_{pp(B)}=E_{C\ (0)}+E_{pp(0)}$$
$$\frac{1}{2}\ \times m\times v_B^2+m\times g\times z_B=\frac{1}{2}\ \times m\times v_0^2+m\times g\times z_0$$
Avec ${\ v}_{finale}={\ v}_B=0$ (le crapaud ne monte plus) ,$\ z_B=z_{max}$ et $z_0=0$
$$0+m\times g\times z_{max}=\frac{1}{2}\ \times m\times v_0^2+0$$
$$z_{max}=\frac{1}{2}\frac{m\times v_0^2}{m\times g}$$
$$z_{max}=\frac{v_0^2}{2g}$$

Q8. En déduire la valeur de la hauteur de barrière minimale, notée Hchampion, qui permet d’arrêter les crapauds les plus puissants, capables de sauter verticalement avec une vitesse initiale v0 de valeur calculée à la question Q6.

$$H_{champion}=z_{max}=\frac{v_0^2}{2g}$$
$$H_{champion}=\frac{{4,4}^2}{2\times9,81}$$
$$H_{champion}=0,99\ m$$

Q9. Les barrières mesurent en réalité 50 à 60 cm de hauteur. Donner un argument permettant d’expliquer pourquoi on choisit d’installer des barrières d’une hauteur inférieure à H_champion.

Dans notre modèle, nous n’avons pas pris en compte les forces de frottement, c’est pourquoi la hauteur des barrières est plus faible que H_champion.