Bac Métropole Mars 2021 Sujet 2
Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet et corrigé
Mots-clés : diffraction et interférences d’ondes lumineuses

Les artémies (voir photo ci-contre) sont des crustacés élevés pour nourrir les poissons des aquariums. Leur taille doit être adaptée à l’espèce de poisson à nourrir. On utilise des tamis calibrés pour les sélectionner.
On se propose dans cet exercice de déterminer la taille des mailles d’un tamis en utilisant une diode laser de longueur d’onde λ = (650 ± 10) nm.
1. Vérification de la valeur de la longueur d’onde de la diode laser utilisée
Pour vérifier la valeur de la longueur d’onde de la diode laser annoncée par le constructeur, on réalise une expérience dont le schéma est donné ci-dessous (figure 1).
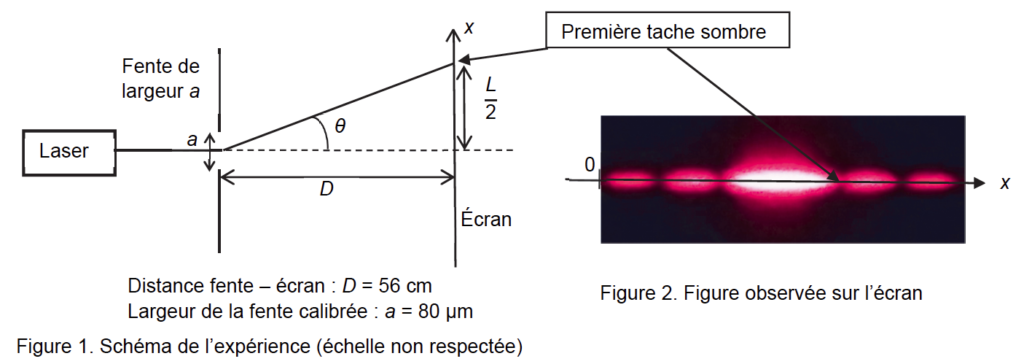
1.1. Nommer le phénomène physique responsable des taches lumineuses observées sur l’écran. Discuter qualitativement de l’influence de la largeur de la fente et de la longueur d’onde de l’onde incidente sur le phénomène observé.
Le phénomène physique responsable des taches lumineuses observées sur l’écran est la diffraction.
Plus la largeur de la fente est petite plus le phénomène est marqué.
Plus la longueur d’onde de l’onde incidente est grande plus le phénomène est marqué.
1.2. On rappelle que l’angle θ est donné par la relation $\theta=\frac{\lambda}{a} $ et on considère que tan θ ≈ θ pour les petits angles (θ << 1 rad). Déterminer l’expression de l’angle θ en fonction de la largeur L de la tache centrale et de D. En déduire l’expression de la longueur d’onde l en fonction de L, a et D.
Lorsque $\theta$ est petit, on considère que $\ tan\ \left(\theta\right)\approx\theta $ et $tan\ (\theta)\ =\frac{L}{2D}$
$$\theta=\frac{L}{2D}$$
Or
$$\theta=\frac{\lambda}{a}$$
D’ou
$$\frac{\lambda}{a}=\frac{L}{2D}$$
$$\lambda=\frac{L \times a}{2D}$$
Pour faire une mesure précise, on remplace l’écran par une caméra qui permet d’obtenir l’intensité lumineuse relative* en fonction de la position x, repérée selon l’axe indiqué sur la photo de la figure 2. L’origine x = 0 m est prise sur le bord du capteur de la caméra. On obtient alors la figure 3.
* L’intensité lumineuse relative est le rapport de l’intensité lumineuse reçue par le capteur sur l’intensité maximale reçue.
1.3. Déterminer la valeur de la longueur d’onde de la diode laser utilisée en exploitant la courbe obtenue sur la figure 3. La comparer à la valeur indiquée par le constructeur.
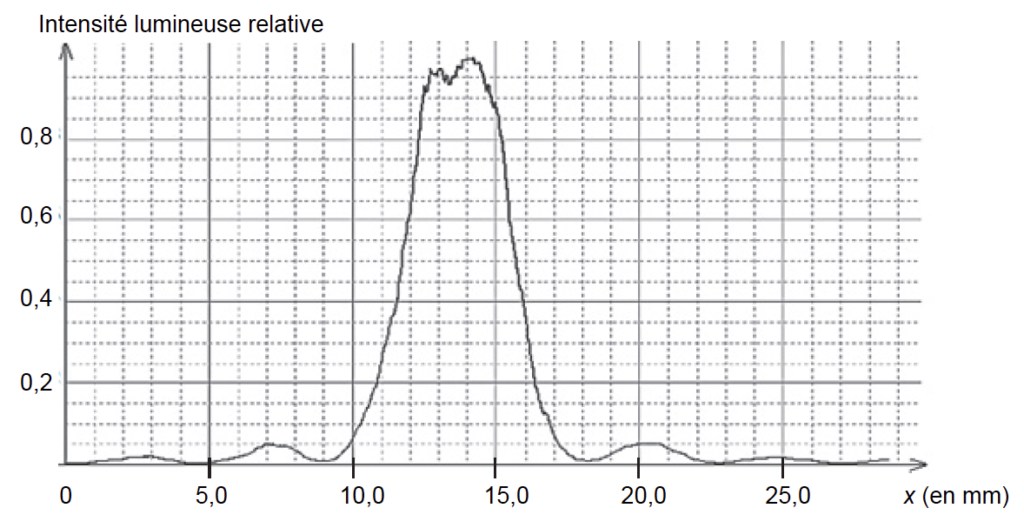

A l’aide de la courbe, on détermine L : L=18,0-9,0=9,0 mm
$$\lambda=\frac{L \times a}{2D}$$
$$\lambda=\frac{9,0 \times {10}^{-3} \times 80 \times {10}^{-6}}{2 \times 56 \times {10}^{-2}}$$
$$\lambda=6,43 \times {10}^{-7}m$$
$$\lambda=643\ nm$$
Valeur indiquée par le constructeur $\lambda=650\ \pm10\ nm $, soit $640\ nm<\lambda<660\ nm$ .
La valeur trouvée $\ \lambda=643\ nm$ se situe dans cet intervalle.
2. Calibrage du tamis de récupération
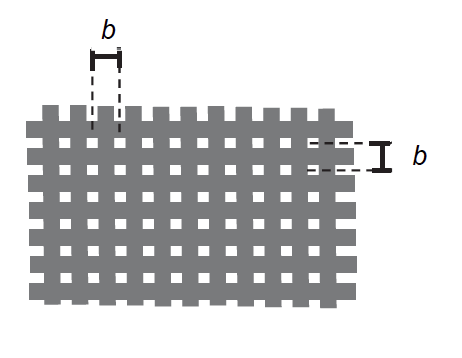
Le but de cette partie est de vérifier que le tamis disponible, dont le maillage est représenté sur la figure 5, permet de récupérer toutes les artémies d’une taille supérieure à 150 µm. On réalise une expérience d’interférences pour évaluer les dimensions du tamis en utilisant la diode laser précédente. La largeur du fil plastique constituant le tamis est égale à 230 µm.
L’expérience d’interférences est décrite ci-dessous :
- le montage utilisé est donné sur la figure 4 ;
- on utilise la diode laser de longueur d’onde λ = (650 ± 10) nm. La distance entre le tamis et l’écran vaut D = (7,75 ± 0,03) m ;
- on note b la distance entre les centres de deux trous consécutifs du maillage du tamis ;
- la figure d’interférences obtenue est donnée sur les figures 6 et 7.
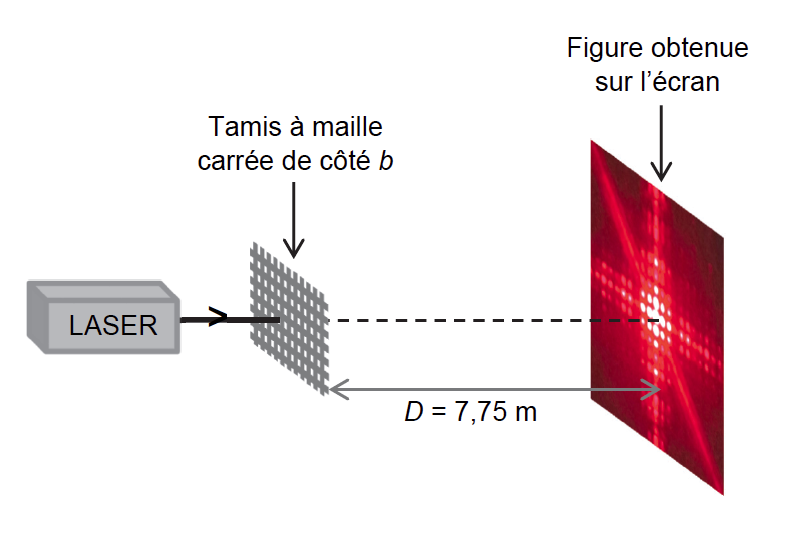


2.1. Expliquer brièvement, sans calcul, l’origine de la présence de zones sombres et de zones brillantes dans une figure d’interférences lumineuses.
La présence de zones sombres est due aux interférences destructives.
La présence de zones brillantes est due aux interférences constructives.
Le centre de la figure d’interférences de la figure 6 est représenté sur la figure 7 ci-dessus à l’échelle 1/1. L’interfrange, noté i, est défini comme la distance entre les centres de deux taches lumineuses successives selon l’axe identifié sur la figure 7.
L’expression de l’interfrange est donnée par la relation : $ i=\frac{\lambda \times D}{b} $
L’incertitude-type u(b) sur la grandeur b peut se calculer à partir de la relation :
$\frac{u(b)}{b}= \sqrt{\left (\frac{u(D)}{D}\right)^2+\left (\frac{u(i)}{i}\right)^2+\left (\frac{u(\lambda)}{\lambda}\right)^2}$
où u(x) désigne l’incertitude-type associée à la grandeur x
2.2. Évaluer la valeur de l’interfrange i en explicitant la méthode suivie pour obtenir la meilleure précision. Évaluer l’incertitude-type u(i) sur la mesure de l’interfrange i.
4i=5,9 cm
$$i=\frac{5,9}{4}$$
i=1,5 cm
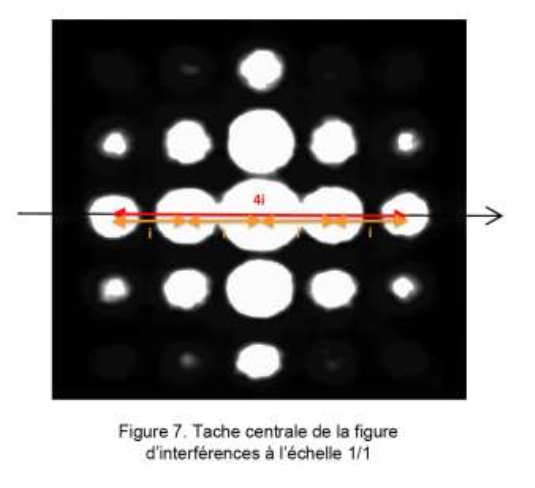
La mesure de l’interfrange i s’effectue à la règle, l’incertitude-type u(i) peut être évaluée comme la moitié d’une graduation soit u(i)=0,5 mm.
2.3. Calculer b puis évaluer u(b).
$$i=\frac{\lambda D}{b}$$
$$b=\frac{\lambda D}{i}$$
$$b=\frac{650 \times {10}^{-9} \times 7,75}{1,5 \times {10}^{-2}}$$
$$b=3,4 \times {10}^{-4}\ m$$
$$\frac{u(b)}{b}=\sqrt{\left(\frac{u(D)}{D}\right)^2+\left(\frac{u(i)}{i}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$
$$u(b)=b \times \sqrt{\left(\frac{u(D)}{D}\right)^2+\left(\frac{u(i)}{i}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$
$$u(b)=3,4 \times {10}^{-4} \times \sqrt{\left(\frac{0,03}{7,75}\right)^2+\left(\frac{0,5 \times {10}^{-3}}{1,5 \times {10}^{-2}}\right)^2+\left(\frac{10}{650}\right)^2}$$
$u\left(b\right)=2 \times {10}^{-5}m$ valeur arrondi à l’excès.
$$b=3,4 \times {10}^{-4}\pm2 \times {10}^{-5}\ m$$
$$b=\left(3,4\pm0,2\right) \times {10}^{-4}\ m$$
2.4. Indiquer si le tamis étudié permet de récupérer les artémies voulues. Justifier.

La largeur du fil plastique constituant le tamis est égale à 230 μm.
$$b=\frac{e}{2}+L+\frac{e}{2}$$
b=e+L
e=b-L
$$e=3,4 \times {10}^{-4}-230 \times {10}^{-6}$$
$$e=1,1 \times {10}^{-4}m$$
$$e=110\ \mu m$$
« Le but de cette partie est de vérifier que le tamis disponible, dont le maillage est représenté sur la figure 5, permet de récupérer toutes les artémies d’une taille supérieure à 150 µm »
Seules les artémies de taille inferieur à 110 μm passent à travers le tamis. Le tamis permet donc de récupérer toutes les artémies d’une taille supérieure à 150 µm.
Remarque : il récupère également les artémies de taille comprise entre 110 et 150 µm.
