Quelques utilisations du condensateur

Liban 2022 Sujet 2

Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée

Sujet n° 22-PYCJ2LR1

Cet exercice s’attache à présenter deux applications des condensateurs.

Partie 1. La balance capacitive

Dans la vie quotidienne, certaines balances électroniques utilisent un capteur à capacité variable afin de mesurer la masse des objets. Pour comprendre le fonctionnement d’un tel dispositif, on envisage dans cette partie une modélisation très simplifiée dans laquelle la balance est modélisée par un condensateur comportant une armature mobile reliée au plateau de pesée et une armature fixe reliée au support de la balance.

Modélisation simplifiée d’une balance de laboratoire

Le modèle étudié est schématisé ci-dessous.

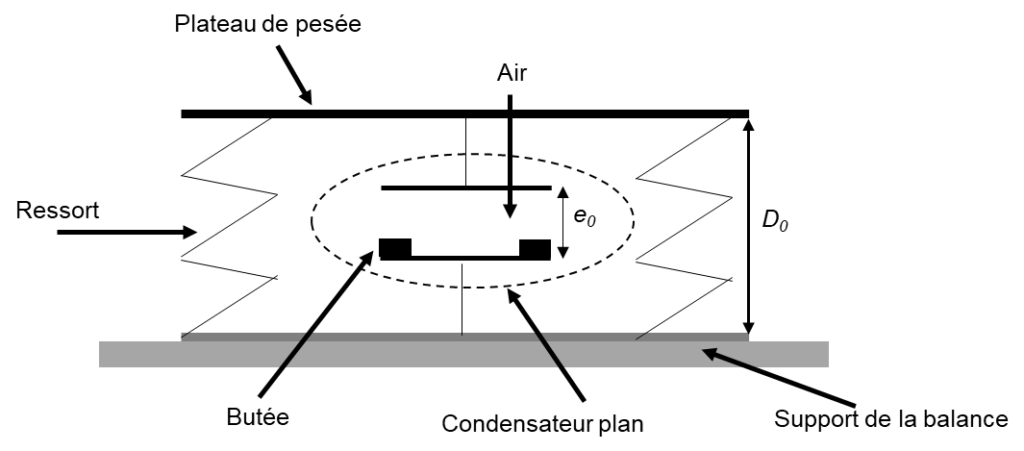
Lorsque la balance est à vide (sans masse sur le plateau), la distance entre les deux armatures est notée e0. Lorsqu’un objet de masse M est posé sur le plateau de pesée, les armatures du condensateur se rapprochent, modifiant alors la valeur de sa capacité C. Les deux armatures ne peuvent pas entrer en contact grâce à la présence de petites butées de taille négligeable devant e₀.

La mesure de la capacité C par un dispositif électronique permet alors de déterminer la masse M de l’objet.

Capacité d’un condensateur plan

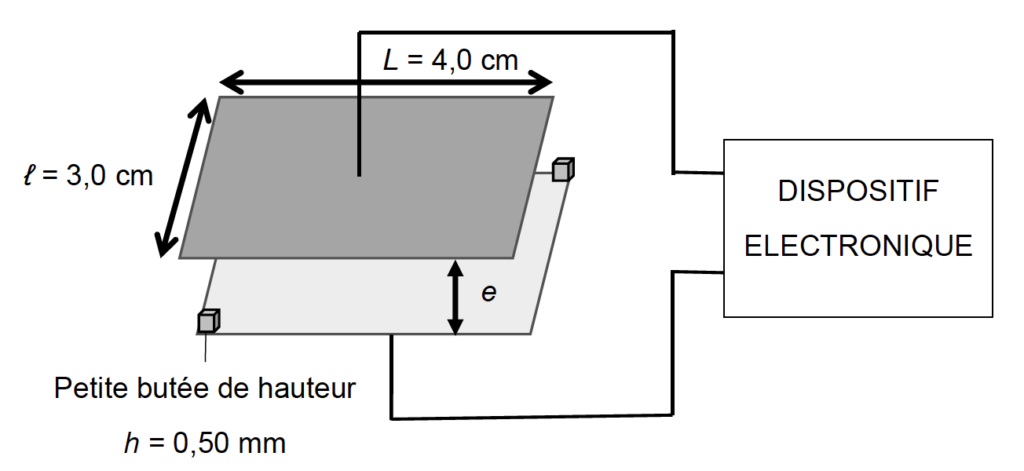
On admet que la capacité du condensateur plan décrit ci-dessus s’écrit : $C=\epsilon_0 \epsilon_R \frac{S}{e}$

Avec :

C : capacité du condensateur en Farad (F) ;
S : superficie des armatures ;
ɛ₀ : permittivité diélectrique du vide ɛ₀ = 8,85×10^-12 F·m^-1 ;
ɛ_r : permittivité diélectrique relative de l’isolant entre les armatures. Pour l’air : ɛ_r = 1,0 ;
e : distance entre les 2 armatures ;
e₀ = 1 cm.

1. Domaine d’utilisation de la balance

1.1. Déterminer la valeur de la capacité C₀ du condensateur lorsque la balance est à vide. On suppose que ɛ_r = 1,0. Commenter.

1.2. Préciser si la capacité du condensateur augmente ou diminue lorsque l’on place une masse sur le plateau. Justifier qualitativement la réponse.

1.3. Lorsqu’un objet de masse M est posé sur le plateau, la distance entre le plateau et le support passe de D0 à D et le plateau exerce sur l’objet une action modélisée par une force F dirigée vers le haut. La valeur de cette force est donnée par la relation :

F = k (D₀ – D) , avec k = 980 N·m^-1.

1.3.1. L’objet de masse M étant à l’équilibre sur le plateau, vérifier que, connaissant la distance D entre le plateau et le support, on peut déduire M par la relation :

$M=\frac{k}{g} (D_0-D)$

où g est l’intensité de la pesanteur : g = 9,8 N·kg^-1.

1.3.2. En admettant que l’armature mobile du condensateur se déplace de la même distance que le plateau lorsqu’un objet de masse M est posé sur celui-ci, calculer la masse maximale que peut mesurer cette balance.

2. Mesure de la masse à peser

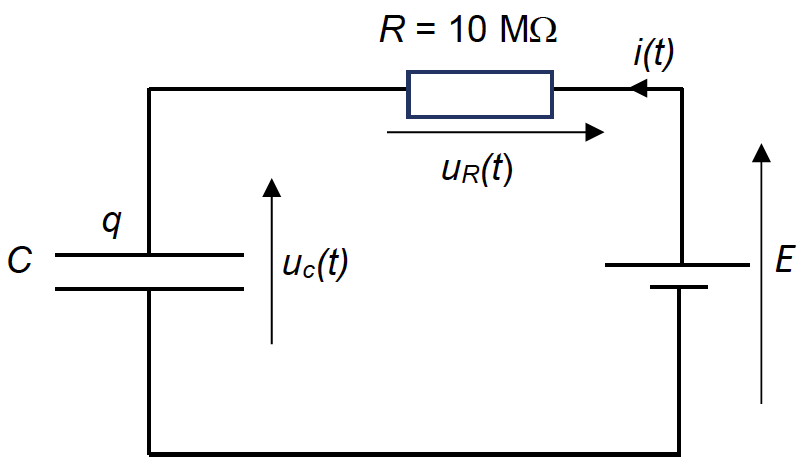
Pour déterminer la valeur de la capacité C du condensateur et en déduire la valeur de la masse immobile sur le plateau, on étudie la charge du condensateur à partir du circuit ci-dessous. À l’instant t = 0, le condensateur est déchargé ; on applique alors au circuit la tension E.

2.1. Montrer que l’équation différentielle vérifiée par la tension aux bornes du condensateur peut s’écrire :

$RC\frac{dU_C(t)}{dt}+U_C(t)=E$

Réponse :

D’après la loi d’additivité des tensions ou loi des mailles :

$E=U_C(t)+U_R(t)$

Or $U_R(t)=r \times i$

$E=U_C(t)+r \times i$

Or $i(t)=\frac{dq(t)}{dt}$

$E=U_C(t)+r \times \frac{dq(t)}{dt}$

Or $q(t)=C \times U_C(t)$

$E=U_C(t)+r \times \frac{C \times U_C(t)}{dt}$

$E=U_C(t)+rC \times \frac{U_C(t)}{dt}$

2.2. Déterminer l’expression de τ en fonction de R et de C pour que la fonction $U_C(t)=E(1-exp(-\frac{t}{\tau}))$ soit solution de l’équation différentielle précédente.

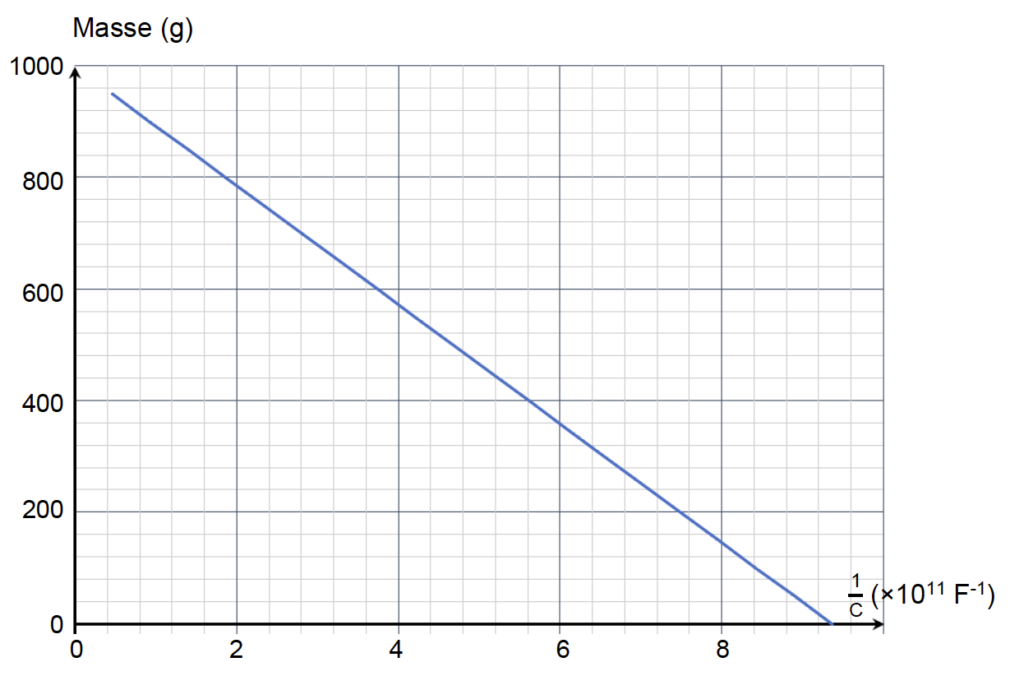
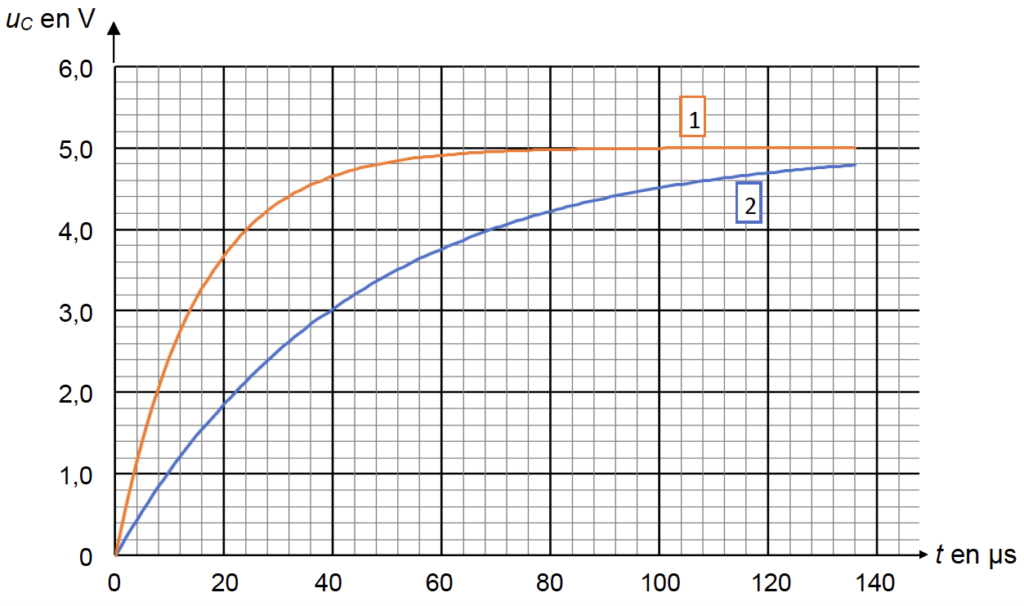
On enregistre les valeurs de la tension u_C(t) aux bornes du condensateur au cours du temps pour deux masses M₁ et M₂ différentes. Les courbes sont fournies en annexe 1 à rendre avec la copie (graphique 1).

2.3. Pour quelle courbe, 1 ou 2, du graphique 1, la valeur de la capacité du condensateur est-elle la plus élevée ? Justifier.

2.4. En exploitant les graphiques 1 et 2, déterminer la valeur de la masse pesée M₂. La méthode utilisée devra être précisée sur les graphiques fournis en annexe 1 à rendre avec la copie.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

Partie 2. Accélérateur linéaire de particules

On s’intéresse dans cette partie à un accélérateur linéaire de particules constitué de blocs métalliques cylindriques séparés par des cavités vides, et comprenant au voisinage de leur axe un passage tubulaire dans lequel les particules chargées peuvent se déplacer.

Les particules, ici des protons, sont accélérées dans les cavités, où règne un champ électrique $\overrightarrow{E}$ . Dans les passages tubulaires, le champ électrique est nul. Toutes les cavités ont la même longueur d.

Dans cet exercice, on étudie le mouvement d’un proton.

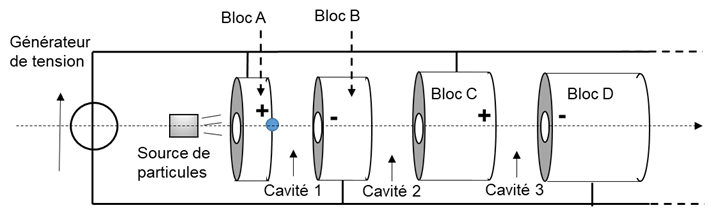
Les protons sont émis par une source avec une vitesse négligeable.

Données :

masse d’un proton : m_p = 1,67×10^-27 kg ;
charge électrique élémentaire : e = 1,60×10^-19 C ;
expression de la norme du vecteur champ électrique : 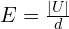$E=\frac{\lvert U \rvert }{d}$ , où U représente la tension entre deux blocs consécutifs et d la distance les séparant.

1. Modélisation par un condensateur plan

L’ensemble constitué par une cavité et deux blocs adjacents peut être modélisé par un condensateur plan (voir schéma ci- contre) relié à un générateur délivrant une tension continue U_AB = 1 kV.

On étudie l’accélération d’un proton à l’intérieur de la cavité.

Un proton de charge q = e entre dans la cavité, en O, à la date t₀ = 0,0 s avec une vitesse initiale nulle et atteint l’armature B au point S avec une vitesse v_S.

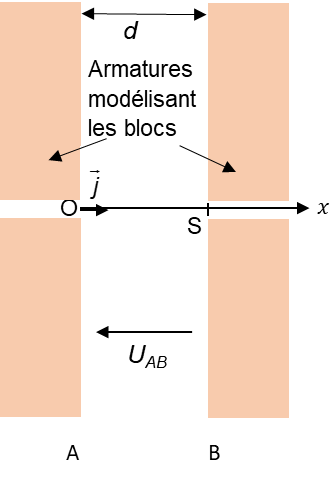
1.1. Préciser le signe des charges portées par les armatures A et B du condensateur si on souhaite que le proton soit accéléré entre ces deux armatures. Justifier la réponse.

1.2. Exprimer la norme F_e de la force électrique modélisant l’action exercée sur le proton entre les armatures du condensateur. Exprimer le résultat en fonction de U_AB, q et d.

On montre que le travail de la force électrique $\overrightarrow{F_e}$ entre les points O et S est : W_OS = q·UAB.

1.3. Exploiter le théorème de l’énergie cinétique pour montrer que la vitesse du proton au point S est

$V_S=\sqrt{ \frac{2qU_{AB}}{m_p}}$ .

1.4. Calculer la valeur de v_S.

2. Constitution de l’accélérateur linéaire de particules

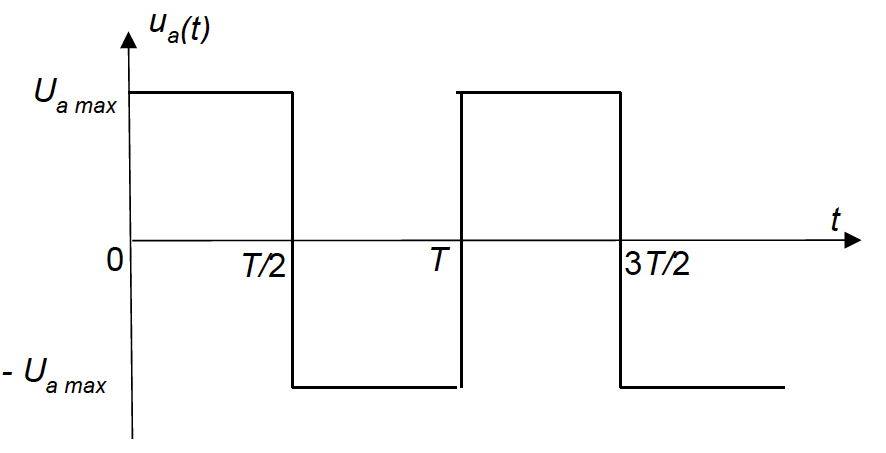
Pour que l’accélération se poursuive dans les différentes cavités, la polarité de chaque tube est alternativement positive et négative : pour cela, le générateur délivre une tension ua(t) alternative de période T = 5,0×10^-7 s.

Les schémas ci-dessous représentent la position du proton à différents instants.

On note d la distance entre deux blocs, L_A la longueur bloc A, L_B la longueur du bloc B, etc.

2.1. Justifier la nécessité de changer le signe de la tension entre les blocs B et C lors du passage de la particule de la première cavité à la deuxième.

Dans un bloc, le mouvement d’une particule est supposé rectiligne uniforme.

2.2. Justifier que le proton doit parcourir la longueur d’un bloc plus la longueur d’une cavité en 2,5×10^-7 s.

2.3. Expliquer qualitativement pourquoi les blocs sont de plus en plus longs dans l’accélérateur linéaire.

Dans les années 1970, l’accélérateur linéaire de protons de Los Alamos (USA), long de 800 m, permettait d’obtenir des protons d’énergie égale à 8,0 MeV à l’aide d’une tension u_a(t) caractérisée par U_{a max} = 1 kV. On rappelle que : 1 eV = 1,6×10^-19 J.

2.4. Déterminer le nombre de cavités accélératrices nécessaires pour qu’un proton atteigne une énergie égale à 8,0 MeV. On considère que le gain en énergie cinétique est identique pour toutes les cavités.

ANNEXE 1 À RENDRE AVEC LA COPIE

Graphique 1. Évolution de la tension u_C(t) aux bornes du condensateur en fonction du temps, pour 2 masses différentes. La courbe 1 correspond à une masse M₁ et la courbe 2 à une masse M₂.

Graphique 2. Courbe d’étalonnage de la masse M pesée en fonction de 1/C.