E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02785, n°G1SPHCH02796 et n°G1SPHCH02799
Télécharger l’exercice en PDF :
Un court-métrage de l’Académie des arts de Suède a attiré l’attention de plus de 1 million d’internautes. Il présente un défi soumis à Robert Förstemann, un coureur cycliste allemand de presque 100 kg, spécialiste de la piste. Le défi qui lui était proposé consistait à faire griller une tranche de pain avec la seule énergie qu’il produisait en pédalant avec ses impressionnantes cuisses de 74 centimètres de circonférence.
L’énergie musculaire du cycliste est transformée en électricité grâce à une dynamo actionnée par la rotation du pédalier. L’ensemble alimente un grille-pain. Pour que l’appareil fonctionne, il faut que le champion produise une puissance de 700 W. Au départ, Robert semble sûr de lui. Au fil du test, le rythme cardiaque de l’athlète augmente, son souffle s’accélère et son visage se creuse sous l’intensité de l’effort qu’il produit. Deux minutes plus tard, le cycliste a fourni au grille-pain 0,021 kWh (76 kJ) suffisant pour sortir une tranche légèrement brunie. Le cycliste s’effondre, incapable de continuer, et s’allonge sur le sol pour récupérer de l’intense effort qu’il vient de produire.
D’après Le Monde (Roland Lehoucq – 14/07/15)
L’objectif de cet exercice est d’étudier la performance physique de Robert Förstemann en la comparant avec la consommation énergétique d’un grille-pain. Enfin, on cherche à évaluer la quantité de sucre à ingérer pour compenser l’énergie fournie lors de cet effort.

1. Performance de Robert Förstemann
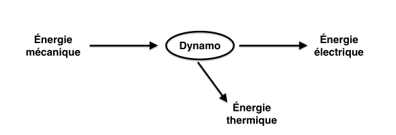
1.1. Schématiser la chaîne énergétique de la dynamo du vélo utilisé par Robert Förstemann. On suppose que le rendement de cette dynamo n’est pas de 100 %.
1.2. Le grille-pain est conçu pour fonctionner normalement sous une tension de 230 V et pour fournir une puissance de 700 W. Montrer que la valeur de l’intensité du courant qui traverse le grille-pain en fonctionnement normal est d’environ 3 A.
$P=U\times I$
$I=\frac{P}{U}$
$I=\frac{700}{230}=3,04\ A$
1.3. Nommer l’effet responsable de l’élévation de température dans le grille-pain. Déduire de la question précédente la valeur de la résistance R du circuit électrique de cet appareil.
L’effet responsable de l’élévation de température dans le grille-pain est l’effet joule.
Pour un conducteur ohmique :
$U=R\times I$
$R=\frac{U}{I}=\frac{230}{3,04}=75,7\Omega$
Une simulation de la caractéristique du circuit électrique du grille-pain est donnée ci-dessous. Elle relie la tension U appliquée à l’intensité du courant électrique I qui traverse le circuit électrique du grille-pain.
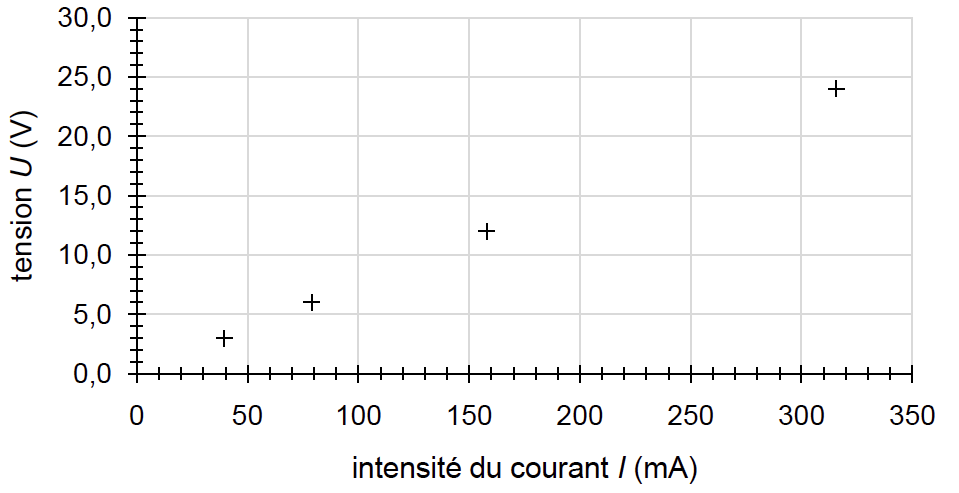
1.4. Indiquer la loi qui modélise la caractéristique du circuit électrique du grille-pain, retrouver la valeur de la résistance du circuit électrique du grille-pain et comparer le résultat à celui de la question précédente.
La courbe est une droite qui passe par l’origine : U et I sont proportionnels.
La loi qui modélise la caractéristique du circuit électrique du grille-pain est la loi d’ohm :
$U=R\times I$
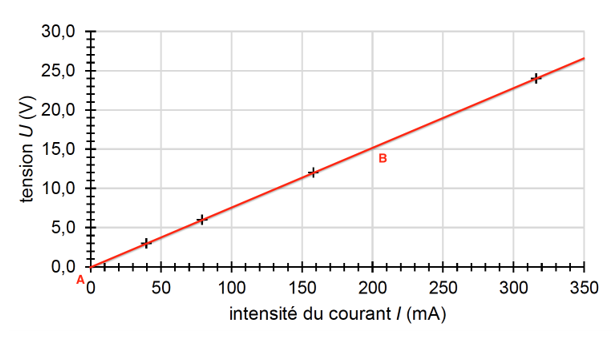
Avec R le coefficient directeur de la droite :
$R=\frac{U_B-U_A}{I_B-I_A}$
$R=\frac{15,0-0}{200.10^{-3}-0}=75,0\ \Omega$
Comparer le résultat à celui de la question précédente :
Ecart relatif :
$\frac{75,7-75,0}{75,7}=0,009=0,9%$
Les deux valeurs sont très proches.
1.5. À partir des données contenues dans l’article du Monde, déterminer la valeur de la puissance moyenne fournie par Robert Forstemann. Estimer, en prenant R = 76 Ω, la valeur moyenne de la tension et de celle de l’intensité du courant de fonctionnement du grille-pain durant la performance. Commenter.
Déterminer la valeur de la puissance moyenne fournie par Robert Forstemann :
« Deux minutes plus tard, le cycliste a fourni au grille-pain 0,021 kWh (76 kJ) »
$E=P\times\Delta t$
$P=\frac{E}{\Delta t}$
$P=\frac{76.10^{3}}{2\times60}=6,3.10^{2}\ W$
Estimer, en prenant $R=76\ \Omega$, la valeur moyenne de la tension :
$P=U\times I$
Or
$U=R\times I$
$I=\frac{U}{R}$
D’ou
$P=\frac{U\times U}{R}$
$P=\frac{U^{2}}{R}$
$U^{2}=P\times R$
$U=\sqrt{P\times R}$
$U=\sqrt{6,3.10^{2}\times76}$
$U=2,2.10^{2}\ V$
L’intensité du courant de fonctionnement du grille-pain durant la performance :
$U=R\times I$
$I=\frac{U}{R}$
$I=\frac{2,2.10^{2}}{76}=2,9\ A$
Commenter : La valeur de l’intensité est proche de celle trouvée à la question 1.2 .
1.6. Estimer, en effectuant un bilan énergétique, la valeur de la vitesse maximale que pourrait atteindre le cycliste à vélo initialement immobile en 5 secondes sur un terrain plat en développant une puissance de 630 W. Commenter.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
$E=P\times\Delta t$
L’énergie produite par le cycliste est de l’énergie cinétique.
$\frac{1}{2}\times m\times v^{2}=P\times\Delta t$
$v^{2}=\frac{2\times P\times\Delta t}{m}$
$v=\sqrt{\frac{2\times P\times\Delta t}{m}}$
« Le candidat est invité à prendre des initiatives » : nous savons que « Robert Förstemann, un coureur cycliste allemand de presque 100 kg ». Nous devons estimer masse du vélo représenté sur la photo : 10 Kg
$v=\sqrt{\frac{2\times630\times5}{110}}=7,6\ m.s^{-1}$
$v=7,6\times3,6=27\ km.h^{-1}$
Commenter : La cycliste doit atteindre une vitesse élevée en seulement 5s.
2. Récupérer après l’effort
Après un effort intense, tel que celui fourni par Robert Förstemann, l’organisme a besoin de glucides simples tels que le saccharose, appelés sucres rapides, disponibles rapidement pour reconstituer les ressources en énergie de l’organisme. Dans cette partie, nous cherchons à déterminer la quantité nécessaire de sucre (saccharose) à ingérer pour récupérer après l’effort fourni par Robert Förstemann.
Le saccharose, sucre de table habituel, est un composé organique de formule brute C12H22O11. Son assimilation par l’organisme s’effectue après son hydrolyse (réaction avec l’eau du saccharose) qui forme du glucose et du fructose, deux sucres de même formule brute.
La molécule de glucose peut adopter une configuration à chaîne ouverte ou cyclique, comme l’illustre les deux représentations du glucose suivantes :

D’après http://www.societechimiquedefrance.fr/saccharose.html
Données :
- 1 cal = 4,18 J ;
- masses molaires atomiques (en g.mol-1) : M(O) = 16 ; M(C) = 12 ; M(H) = 1 ;
- une boîte de sucre de masse nette m = 1,0 kg contient 168 morceaux ;
- l’énergie molaire fournie par la combustion (oxydation complète) du saccharose est 5,8×106 J·mol-1 ;
- bandes d’absorption IR de quelques liaisons chimiques :
| famille | liaison | nombres d’onde (cm-1) |
| cétone | C = O | 1705 – 1725 |
| aldéhyde | Ctri – H C = O | 2700 -2900 1720 – 1740 |
| acide carboxylique | O – H C = O | 2500 – 3200 1740 – 1800 |
| ester | C = O | 1730 – 1750 |
| alcool | O – Hlié O – Hlibre | 3200 – 3450 3600 – 3700 |
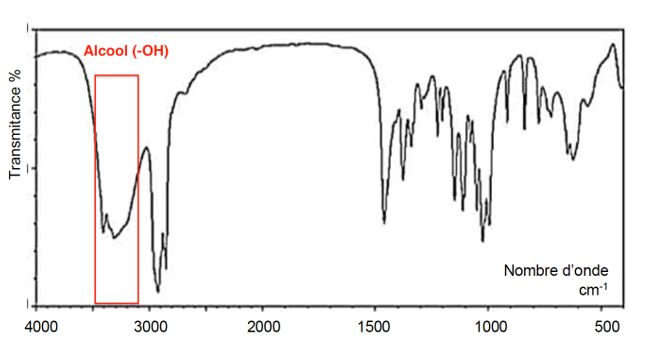
2.1. Le spectre infrarouge obtenu par analyse d’un échantillon de glucose est fourni ci-dessous. Déduire de ce spectre la configuration majoritaire du glucose dans l’échantillon étudié. Justifier.
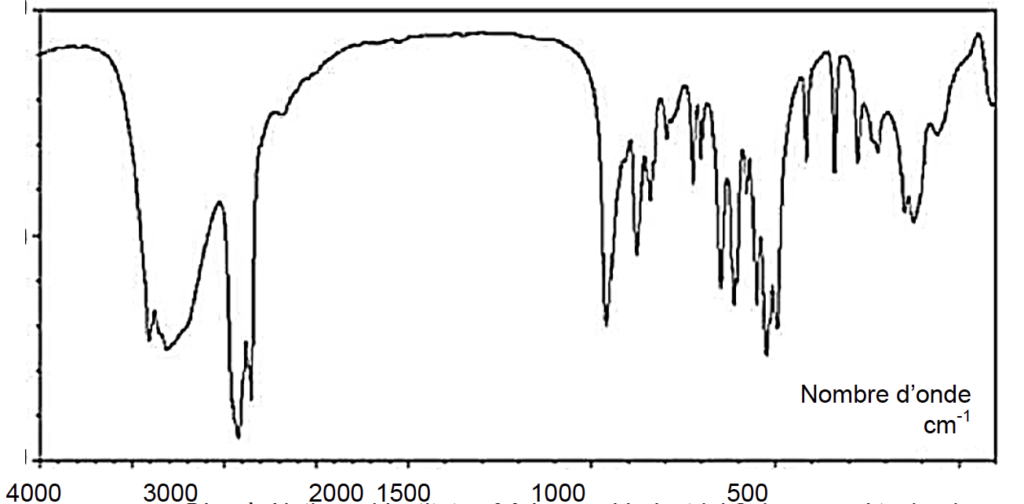
D’après Nationnal Institute of Advanced Industrial Science and technology – htpp://sdbs.aist.go.jp
| Molécule | Familles présentes dans la molécule | Nombres d’onde (cm-1) attendus |
chaîne ouverte 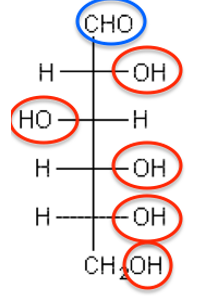 | Alcool (-OH) Aldéhyde (-HC=O) | 3200 – 3450 ou 3600 – 3700 2700 -2900 et 1720 – 1740 |
chaîne cyclique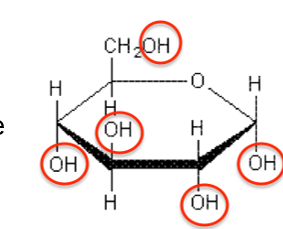 | Alcool (-OH) | 3200 – 3450 ou 3600 – 3700 |
La spectroscopie IR permet de déterminer la famille de la molécule analysée. Les deux molécules possèdent des groupes hydroxyles de la famille des alcools. Cependant, seul le glucose à chaîne ouverte possède un groupe carbonyle de la famille des aldéhydes.
Sur ce spectre on remarque la présence de la bande du aux liaisons –OH et l’absence de bandes dues à l’aldéhyde.
La configuration majoritaire du glucose dans l’échantillon étudié est donc celle du glucose à chaîne cyclique.
2.2. Écrire l’équation de la réaction modélisant l’hydrolyse du saccharose.
« Hydrolyse (réaction avec l’eau du saccharose) qui forme du glucose et du fructose, deux sucres de même formule brute. »
$C_{12}H_{22}O_{11}+H_{2}O\rightarrow C_{6}H_{12}O_{6}+C_{6}H_{12}O_{6}$
2.3. Vérifier que l’oxydation complète d’un morceau de sucre libère une énergie d’environ 24 kcal.
« L’énergie molaire fournie par la combustion (oxydation complète) du saccharose est $5,8\times10^{6}\ J.mol^{-1}$ »
$E=n_{saccharose}\times E_{molaire}$
Or
$n_{saccharose}=\frac{m_{saccharose}}{M_{saccharose}}$
d’ou
$E=\frac{m_{saccharose}}{M_{C_{12}H_{22}O_{11}}}\times E_{molaire}$
« Une boîte de sucre de masse nette $m=1,0\ kg$ contient 168 morceaux »
soit
$m=\frac{1,0.10^{3}}{168}=5,95\ g$
$M_{C_{12}H_{22}O_{11}}=12\times M_C+22\times M_H+11\times M_O$
$E=\frac{5,95}{12\times12+22\times1+11\times16}\times5,8.10^{6}=1,0.10^{5}\ J$
$1\ cal=4,18\ J$
$E=\frac{1,0.10^{5}}{4,18}=2,4.10^{4}\ cal=24\ kcal$
2.4. En déduire la quantité de sucre que Robert Förstemann doit ingérer pour compenser l’effort réalisé en supposant que l’énergie musculaire a été intégralement transférée au grille-pain. Commenter.
« Le cycliste a fourni au grille-pain 0,021 kWh (76 kJ) »
| Nombre de carreaux | Energie |
| 1 carreau | $1,0.10^{5}\ J$ |
| x | 76 kJ |
$x=\frac{76.10^{3}\times1}{1,0.10^{5}}=0,76\ carreau$
Robert Förstemann doit ingérer 0,76 sucre environ les (¾ d‘un carreau) pour compenser l’effort réalisé.
