Centres étrangers 2025 Sujet 1
Exercice 2 – (6 points) – Durée 1h03 – Calculatrice autorisée
Sujet n°25-PYCJ1G11
Sujet et corrigé
EXERCICE 2 : RADAR PÉDAGOGIQUE ÉQUIPÉ D’UN PANNEAU SOLAIRE (6 POINTS)
Le radar pédagogique est un équipement implanté en bordure de chaussée pour indiquer à l’usager :
- la vitesse à laquelle il circule,
- un message d’alerte si sa vitesse est supérieure à celle qui est autorisée.
Un radar pédagogique (figure 1) est composé de plusieurs éléments :
– un panneau solaire photovoltaïque.
– un support de fixation rigide ;
– un caisson comportant un écran pour l’affichage ;
– un capteur permettant de détecter les véhicules en circulation ;
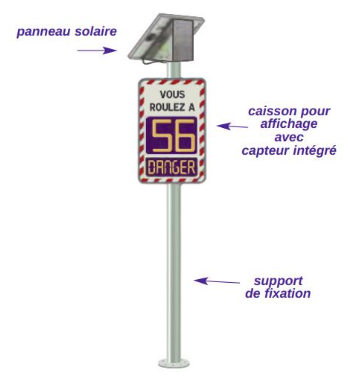
Figure 1. Ensemble des éléments qui constituent un radar pédagogique
Données :
– Panneau solaire photovoltaïque :
• dimensions : 850 mm x 950 mm ;
• puissance lumineuse reçue : Plum = E×S avec E l’éclairement en W·m-2 et S la surface du panneau en m2 ;
• rendement annoncé : 20 % ;
– Éclairement moyen dans la commune où est placé le radar : E = 600 W·m-2.
Dans un premier temps, cet exercice s’intéresse au panneau solaire photovoltaïque qui assure l’alimentation électrique du radar pédagogique puis, dans un second temps, au fonctionnement du radar pour mesurer la vitesse d’un véhicule.
1. Alimentation électrique du radar : le panneau solaire photovoltaïque
Associé à une batterie, le radar est alimenté électriquement grâce à un panneau solaire photovoltaïque.
Afin de vérifier le rendement du panneau, on réalise le montage électrique suivant :
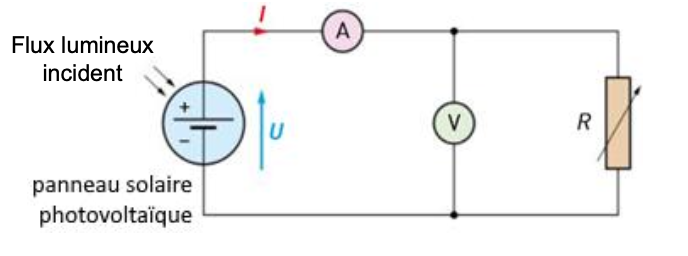
Figure 2. Schéma électrique
L’intensité I du courant électrique ainsi que la tension électrique U aux bornes du panneau sont mesurées. Les graphiques de la figure 3 représentent, pour différents éclairements, l’évolution de l’intensité I et de la puissance électrique P fournis par le panneau en fonction de la tension U aux bornes du panneau :

Figure 3. Caractéristiques du panneau photovoltaïque
Q.1. Justifier, en utilisant la figure 3, le fait que dans les conditions d’éclairement du radar, la puissance électrique maximale fournie est $P_m = 100\ \text{W}$.
D’après le sujet : « Éclairement moyen dans la commune où est placé le radar : E = 600 W·m-2 »
Graphiquement, pour un Éclairement E = 600 W·m-2, la puissance électrique maximale fournie est Pm = 100 W.

Q.2. Calculer la valeur du rendement $\eta$ du panneau photovoltaïque. Conclure.
$$\eta=\frac{P_m}{P_{lum}}$$
Or
$P_{lum}=E\times S$
D’où :
$$\eta=\frac{P_m}{E\times S}$$
$$\eta=\frac{100}{600\times 850\times 10^{-3}\times 950\times 10^{-3}}$$
$$\eta=0,21$$
$$\eta=21%$$
D’après le sujet : « rendement annoncé : 20 % ; »
Le rendement calculé est conforme au rendement annoncé.
2. Fonctionnement du radar
Un capteur radar est constitué d’un émetteur et d’une antenne réceptrice.
L’émetteur lance de très brefs signaux électromagnétiques dans le domaine des micro-ondes à la fréquence fE.
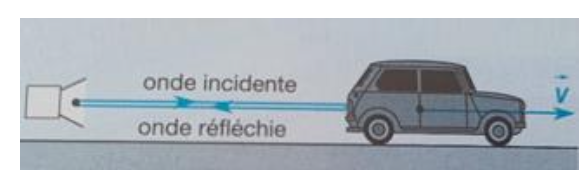
Figure 4. Schéma de principe de fonctionnement d’un radar
Les véhicules situés dans le champ de l’émetteur réfléchissent les signaux reçus, qui sont ensuite captés par l’antenne. Celle-ci détermine la fréquence fR du signal reçu.
Q.3. Décrire qualitativement l’effet Doppler.
L’effet Doppler est la variation apparente de la fréquence d’une onde perçue par un observateur, due au mouvement relatif entre la source et l’observateur. Si la source s’approche, la fréquence perçue augmente (son plus aigu) ; si elle s’éloigne, la fréquence diminue (son plus grave).
Dans le cadre d’une étude expérimentale réalisable en classe, le capteur radar est modélisé par un émetteur E et un récepteur R d’ondes ultrasonores, fixes et placés l’un à côté de l’autre sur un banc. Une plaque modélisant le véhicule en déplacement est fixée sur un chariot mobile.

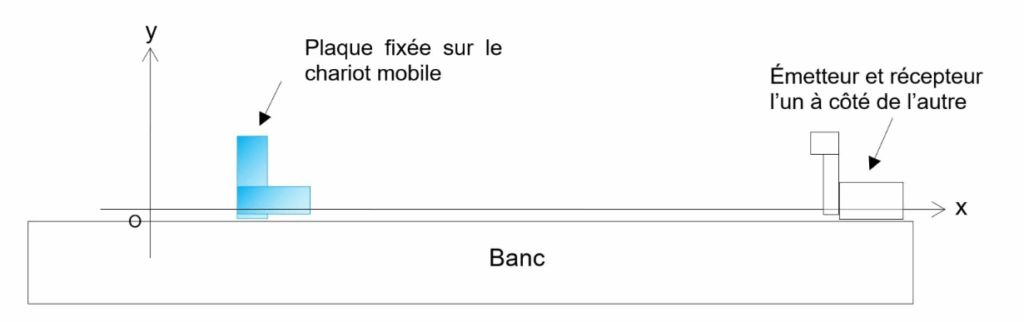
Figure 5. Dispositif expérimental
Le chariot mobile se déplace horizontalement le long du banc, dans le référentiel terrestre supposé galiléen.
Données :
- Température de l’air à l’intérieur de la pièce : θ = 21,0°C
- Dans tout l’exercice :
- les forces de frottements exercées par l’air et le banc sur le chariot sont négligées ;
- la vitesse de déplacement du chariot vchariot est supposée constante.
- Vitesse de propagation v des ondes sonores dans l’air en fonction de la température :
| θ (°C) | 15,0 | 16,0 | 17,0 | 18,0 | 19,0 | 20,0 | 21,0 | 22,0 |
| v (m·s-1) | 340,61 | 341,21 | 341,82 | 342,43 | 343,03 | 343,64 | 344,25 | 344,85 |
- Expression du décalage Doppler pour le capteur radar : $\Delta f = 2\times f_E\times \frac{v_{chariot}}{v}$ avec $f_E$ et $\Delta f$ en Hz, $v_{chariot}$ et $v$ en m·s$^{-1}$.
Mesure de la vitesse du chariot grâce à un pointage
Le pointage à intervalles de temps réguliers d’un point du chariot, matérialisé par le « + » (figure 6), est réalisé afin d’obtenir la trajectoire du chariot (figure 7).

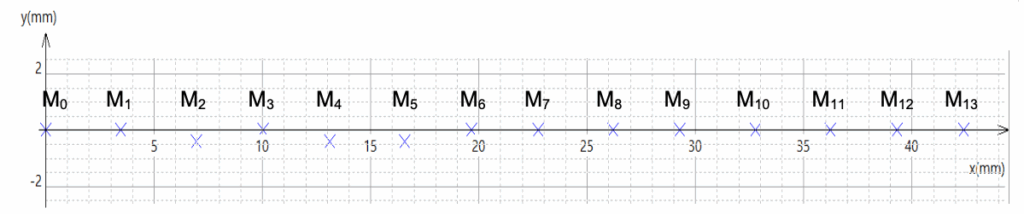
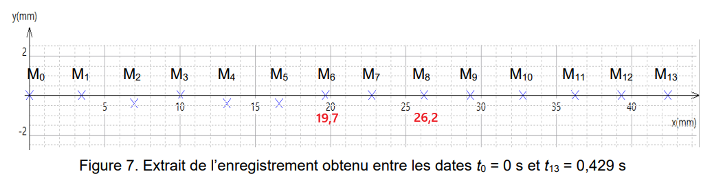
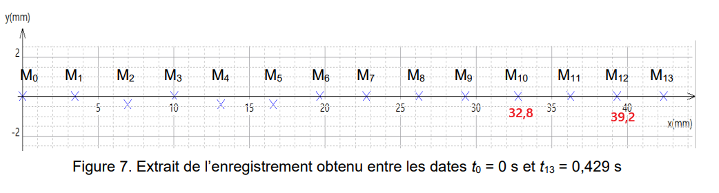
Figure 7. Extrait de l’enregistrement obtenu entre les dates t0 = 0 s et t13 = 0,429 s
Q.4. Calculer les valeurs des vitesses $v_7$ et $v_{11}$ du chariot respectivement aux dates $t_7$ et $t_{11}$.
D’après le sujet : t0 = 0 s et t13 = 0,429 s
Calculons le temps entre deux positions :
$$\tau=\frac{t_{13}-t_0}{13}$$
$$\tau=\frac{0,429-0}{13}$$
$$\tau=3,3\times 10^{-2}\ \mathrm{s}$$
Pour calculer la vitesse on utilise la formule :
$v_i=\frac{M_{i-1}M_{i+1}}{2\tau}$
$$v_7=\frac{26,2\times 10^{-3}-19,7\times 10^{-3}}{2\times 3,3\times 10^{-2}}$$
$$v_7=9,85\times 10^{-2}\ \mathrm{m·s^{-1}}$$
$$v_{11}=\frac{39,2\times 10^{-3}-32,8\times 10^{-3}}{2\times 3,3\times 10^{-2}}$$
$$v_{11}=9,70\times 10^{-2}\ \mathrm{m·s^{-1}}$$
Le traitement des données acquises permet de tracer l’évolution temporelle de deux grandeurs ; la position x (en m) et la vitesse horizontale vx (en m·s-1) du chariot : x = f(t) et vx = g(t) (figures 8a et 8b).
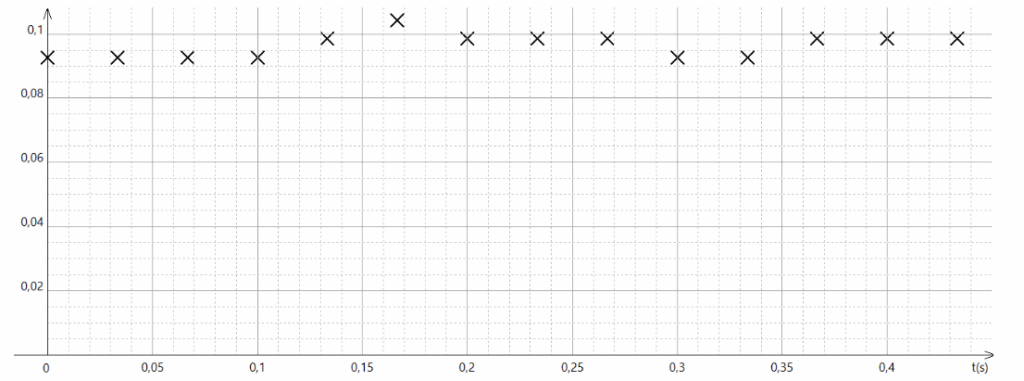
Figure 8a. Courbe A
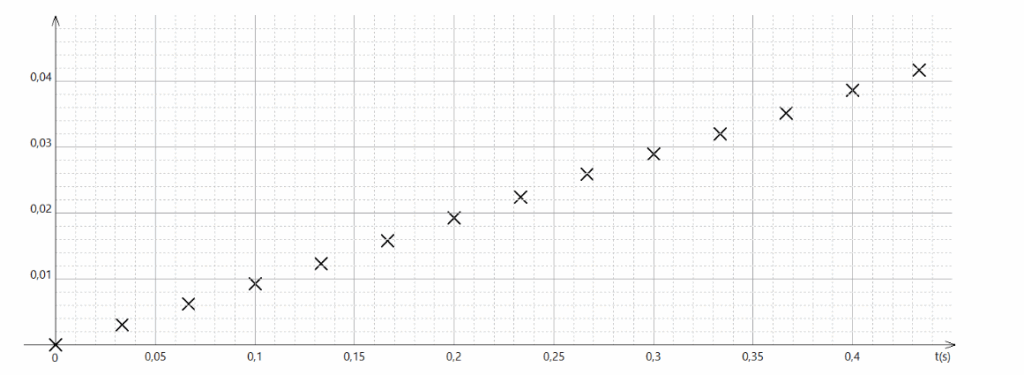
Figure 8b. Courbe B
Q.5. Associer, en justifiant, chaque courbe A et B des figures 8a et 8b à la grandeur correspondante.
D’après le sujet : « Le traitement des données acquises permet de tracer l’évolution temporelle de deux grandeurs ; la position x (en m) et la vitesse horizontale vx (en m·s-1) du chariot : x = f(t) et vx = g(t) (figures 8a et 8b). »
Au cours du temps, le chariot se déplacé, sa position x augmente : Figure 8b.
Les vitesses calculées précédemment sont similaires et leurs valeurs correspondent aux valeurs portées sur la figure 8a.
la vitesse horizontale vx est représentée figure 8a.
Q.6. Estimer, à partir d’une des figures 8a ou 8b, la valeur de la vitesse moyenne du chariot.
Méthode 1 :
Graphiquement, sur la figure 8a, on lit :
$$v_{moy}=0,096\ \mathrm{m·s^{-1}}$$
$$v_{moy}=9,6\times 10^{-2}\ \mathrm{m·s^{-1}}$$

Méthode 2 :
$v_x=\frac{dx}{dt}$
Or une dérivée est le coefficient directeur de la tangente à la courbe.
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{0,04-0}{0,41-0}$$
$$k=9,8\times 10^{-2}\ \mathrm{m·s^{-1}}$$
D’où
$v_x=k=9,8\times 10^{-2}\ \mathrm{m·s^{-1}}$

Mesure de la vitesse du chariot grâce à l’effet Doppler
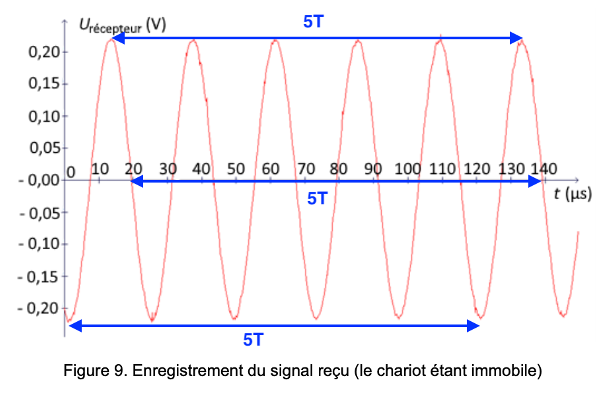
Le signal reçu par le récepteur d’ondes ultrasonores lorsque le chariot reste immobile est enregistré. La courbe obtenue de la tension aux bornes du récepteur en fonction du temps est représentée ci-dessous (figure 9).

Figure 9. Enregistrement du signal reçu (le chariot étant immobile)
Q.7. Déterminer la valeur de la période $T_R$ du signal obtenu. En déduire que la valeur de la fréquence $f_E$ du signal émis par l’émetteur vaut $42\ \text{kHz}$.
Graphiquement :
$$5T_R=140-20$$
$$5T_R=120\ \mu s$$
$$T_R=\frac{120}{5}$$
$$T_R=24\ \mu s$$
Calculons la fréquence reçue :
$$f_R=\frac{1}{T_R}$$
$$f_R=\frac{1}{24\times 10^{-6}}$$
$$f_R=4,2\times 10^{4}\ \mathrm{Hz}$$
$$f_R=42\ \mathrm{kHz}$$
Lorsque l’émetteur et le récepteur sont immobiles l’un par rapport à l’autre, il n’y a pas d’effet Doppler :
$$f_E=f_R$$
$$f_E=42\ \mathrm{kHz}$$
Ainsi, la valeur de la fréquence $f_E$ du signal émis par l’émetteur vaut $42\ \mathrm{kHz}$.
Une nouvelle acquisition du signal émis et du signal reçu est réalisée lorsque le chariot se déplace, en se rapprochant de l’émetteur et du récepteur. Le décalage Doppler mesuré est Δf = 22,7 Hz.
Q.8. Calculer la valeur de vchariot, la vitesse du chariot obtenue par effet Doppler. Comparer le résultat obtenu à ceux des questions Q.4 et Q.6.
Expression du décalage Doppler pour le capteur radar :
$$\Delta f = 2\times f_E \times \frac{v_{chariot}}{v}$$
D’après le sujet : « Température de l’air à l’intérieur de la pièce : $\theta = 21,0^{\circ}\mathrm{C}$ ».
Pour $\theta=21,0^{\circ}\mathrm{C}$, on lit sur le tableau : $v = 344,25\ \mathrm{m·s^{-1}}$

Calculons $v_{chariot}$ :
$$v_{chariot}=\Delta f\times \frac{v}{2\times f_E}$$
$$v_{chariot}=22,7\times\frac{344,25}{2\times 42\times 10^{3}}$$
$$v_{chariot}=9,3\times 10^{-2}\ \mathrm{m·s^{-1}}$$
Le résultat obtenu $9,3\times 10^{-2}\ \mathrm{m·s^{-1}}$ est du même ordre de grandeur que ceux des questions Q4 et Q6.
