E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02788, n°G1SPHCH02792 et n°G1SPHCH02799
Télécharger l’exercice en PDF :
Les ressources d’énergie renouvelables (solaire, éolien, etc…) présentent un problème d’intermittence car elles sont dépendantes des phénomènes météorologiques. Pour résoudre ce problème une stratégie consiste à stocker l’énergie produite dans les périodes favorables afin de pouvoir la réutiliser quand les conditions météorologiques ne permettent pas une production suffisante.
On propose dans cette partie d’étudier deux stratégies de stockage :
- un stockage chimique par transformation du dioxyde de carbone de l’atmosphère en méthane ;
- un stockage physique à l’aide du remplissage d’un bassin de rétention d’eau.
I. Étude du stockage chimique de l’énergie
Le Professeur K. Hashimoto (Université de Sendai, Japon) a développé un procédé qui transforme le dioxyde de carbone en méthane en utilisant un électrolyseur à eau de mer et des catalyseurs. Les électrolyseurs sont alimentés par l’énergie solaire.
Le méthane produit peut ensuite servir de carburant afin de faire fonctionner un générateur électrique. Ce dernier fonctionne sur le principe suivant : l’énergie thermique libérée par la combustion du méthane permet de produire de la vapeur d’eau qui actionne une turbine. Un alternateur permet alors de produire de l’électricité. Un schéma de principe du dispositif est représenté ci-dessous.
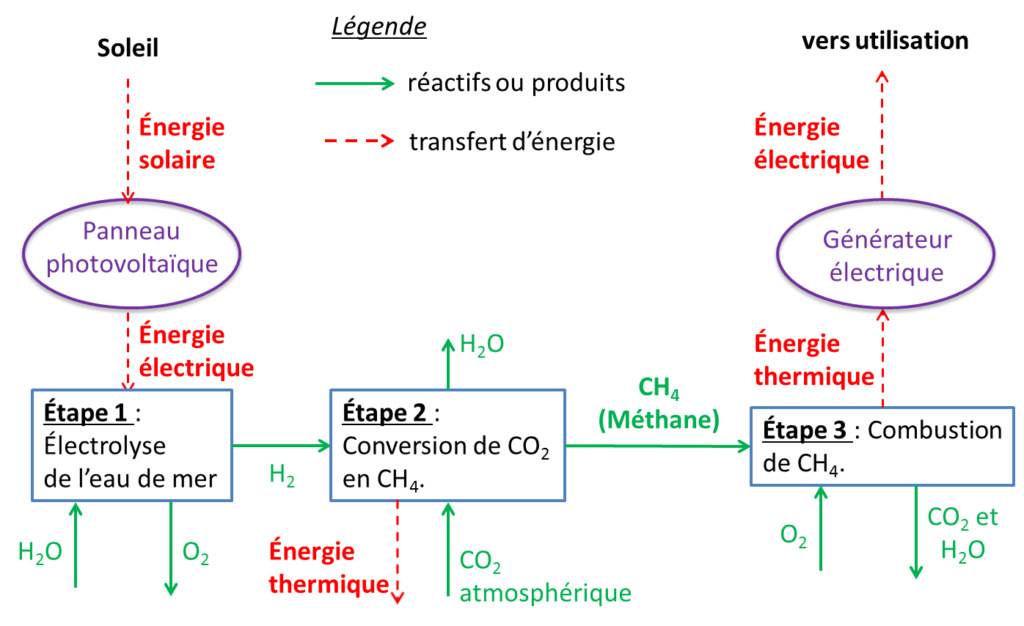
Il se produit dans les différentes étapes les transformations chimiques modélisées par les réactions chimiques d’équation :
- étape 1 : H2O (l) → H2(g)+1/2 O2(g) ;
- étape 2 : CO2(g) +4 H2(g)→CH4 (g) +2 H2O (g) ;
- étape 3 : combustion complète du méthane.
Problématique 1 : en quoi le procédé de transformation du dioxyde de carbone en méthane peut-il permettre de répondre aux difficultés liées au caractère intermittent des énergies renouvelables ?
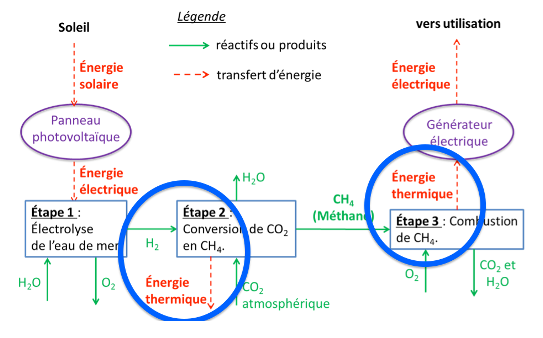
1. Justifier pour chacune des étapes 2 et 3 du procédé si elle est endothermique ou exothermique.
Les étapes 2 et 3 libèrent de l’énergie thermique. Elles sont donc exothermiques.
2. Écrire l’équation de la réaction de combustion complète du méthane de formule brute CH4.
$$CH_4+2O_2\rightarrow CO_2+2H_2O$$
On cherche à estimer le pouvoir calorifique massique du méthane. Pour cela on mesure la masse de méthane nécessaire pour porter à l’ébullition une masse d’eau meau = 1,00 kg dont la température initiale est Ti = 20,2 °C. La manipulation est réalisée 6 fois avec le même dispositif.
On rappelle que le pouvoir calorifique massique du méthane est défini par la relation :
$P_C=\frac{E_{libérée}}{m_{méthane consommé}}$ avec Elibérée l’énergie libérée lors de la combustion d’une masse de méthane mméthane consommé. Les résultats sont reportés dans le tableau ci-dessous.
| Essais | N°1 | N°2 | N°3 | N°4 | N°5 | N°6 |
| Masse de méthane consommée (en g) | 12,1 | 10,9 | 11,6 | 11,0 | 11,8 | 10,9 |
L’énergie libérée par la combustion peut être déterminée par la relation :
$E_{libérée}=m_{eau}\times C_{eau}\times (T_f-T_i)$
avec :
- ceau la capacité thermique massique de l’eau liquide : ceau = 4,18 kJ.kg-1.K-1.
- Tf la température finale de l’eau, c’est-à-dire la température d’ébullition de l’eau dans les conditions de l’expérience Tf = 100,0 °C.
Pour effectuer le calcul du pouvoir calorifique massique à partir des résultats expérimentaux, il est nécessaire de déterminer une masse expérimentale de méthane consommée. Pour cela, on fait la moyenne sur toutes les valeurs de masse (valeurs n°1 à n°6).
3. Montrer, en détaillant les calculs, que la valeur expérimentale obtenue pour le pouvoir calorifique massique PC du méthane est de l’ordre de 29 MJ.kg-1.
Le pouvoir calorifique massique du méthane est défini par la relation :
$P_c=\dfrac{E_{libérée}}{m_{méthane\ consommée}}$
Or
$E_{libérée}=m_{eau}\times c_{eau}\times(T_f-T_i)$
$m_{méthane\ consommée}=m_{méthane\ consommée\ moyenne}=m_1+m_2+m_3+m_4+m_5+m_6$
D’ou
$$P_c=\dfrac{m_{eau}\times c_{eau}\times\left(T_f-T_i\right)}{\left(\dfrac{m_1+m_2+m_3+m_4+m_5+m_6}{6}\right)}$$
$$P_c=\dfrac{1,00\times4,18.10^3\times\left(100-20,2\right)}{\left(\dfrac{\left(12,1+10,9+11,6+11,0+11,8+10,9\right)\times10^{-3}}{6}\right)}$$
$$P_c=2,93.10^7\ J.kg^{-1}$$
$$P_c=29,3\ MJ.kg^{-1}$$
La valeur de référence du pouvoir calorifique massique du méthane est 50 MJ.kg-1.
4. Proposer une explication pour interpréter l’écart entre la valeur expérimentale du pouvoir calorifique massique du méthane et sa valeur de référence.
« La valeur de référence du pouvoir calorifique massique du méthane est 50 MJ.kg-1. »
Expérimentalement nous avons obtenu nos résultats en considérant que l’intégralité de l’énergie de la combustion du méthane qui a été transférée de l’eau. Or lorsque le méthane brule il chauffe l’air ambiant, les parois du dispositif contenant l’eau…
C’est pourquoi on obtient un écart entre la valeur expérimentale du pouvoir calorifique massique du méthane et sa valeur de référence.
On considère que :
- la production d’un kilogramme de méthane par les étapes 1 et 2 du procédé nécessite 117 MJ d’énergie intermittente ;
- seuls 25 % de l’énergie thermique libérée par la combustion du méthane est transformée en électricité.
5. Répondre à la problématique 1 en déterminant la proportion d’énergie intermittente pouvant être considérée comme ayant été stockée par ce procédé. On utilisera la valeur de référence du pouvoir calorifique massique du méthane.
Déterminons la proportion d’énergie intermittente pouvant être considérée comme ayant été stockée par ce procédé :
$P=\dfrac{E_{electrique}}{E_{énergie\ intermittente}}\times100$
Avec : $E_{electrique}=\dfrac{25}{100}\times50$, car seuls 25 % de l’énergie thermique libérée par la combustion du méthane est transformée en électricité.
$$P=\dfrac{\dfrac{25}{100}\times50}{117}\times100$$
$$P=10,7%$$
« Problématique 1 : en quoi le procédé de transformation du dioxyde de carbone en méthane peut-il permettre de répondre aux difficultés liées au caractère intermittent des énergies renouvelables ? »
Bien que le pourcentage d’énergie intermittente pouvant être considérée comme ayant été stockée par ce procédé soit faible, il permet de stocker de l’énergie pouvant être utilisée à tout moment et répond donc aux difficultés liées au caractère intermittent des énergies renouvelables.
II. El Hierro : île pionnière de l’énergie renouvelable
Le pompage-turbinage est une technique de stockage de l’énergie électrique permettant de palier l’intermittence des ressources d’énergie renouvelables. Lorsque les conditions météorologiques sont favorables, l’excédent d’énergie produit par les éoliennes est utilisé pour faire fonctionner des pompes permettant de remplir des retenues d’eau situées en altitude. Lorsque la production d’électricité devient insuffisante, les retenues d’eau sont ouvertes. Après une chute de 650 m à travers une conduite forcée, l’eau actionne des turbines hydroélectriques qui entrainent un alternateur afin de produire de l’électricité.
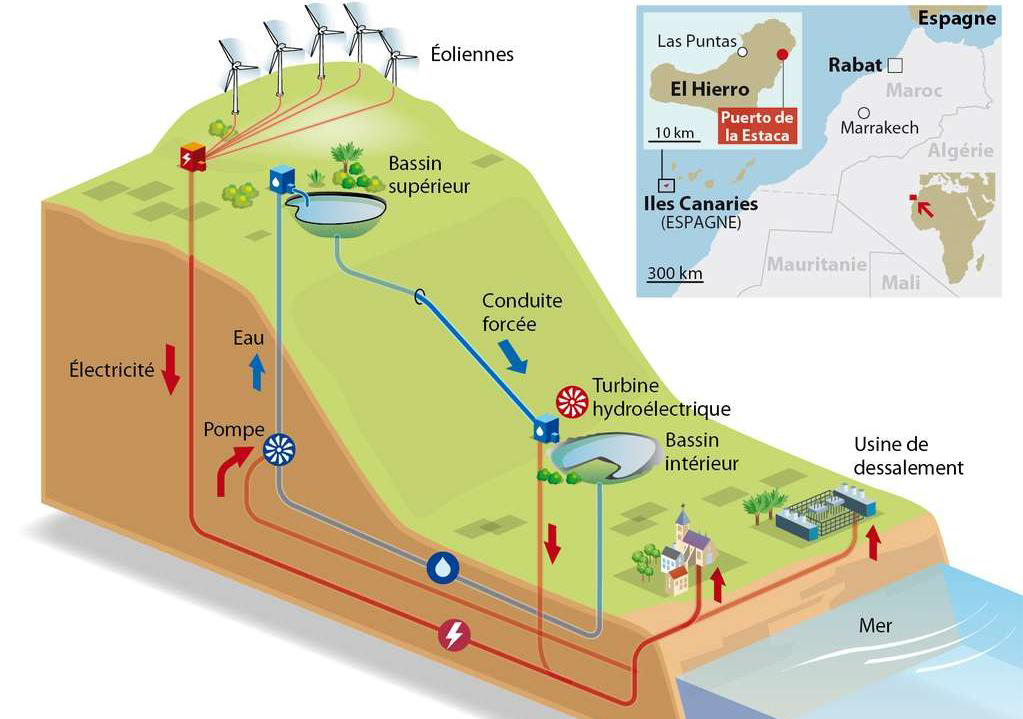
Source : Futura-Sciences https://www.futura-sciences.com/planete/actualites/developpement-durable-ile-el-hierro-bientot-totalement-autonome-energie-44372/
Problématique 2 : en quoi les infrastructures de l’île de El Hierro lui permettent-elle de s’affranchir des énergies fossiles ?
On s’intéresse à l’eau contenue dans le réservoir supérieur qui chute à travers la conduite forcée pour remplir le bassin inférieur. Le volume d’eau utile considéré est donc égal au volume du réservoir inférieur Vinf et la masse de ce volume d’eau utile, notée M, chute via la conduite du point A au point B (voir schéma ci-dessous).
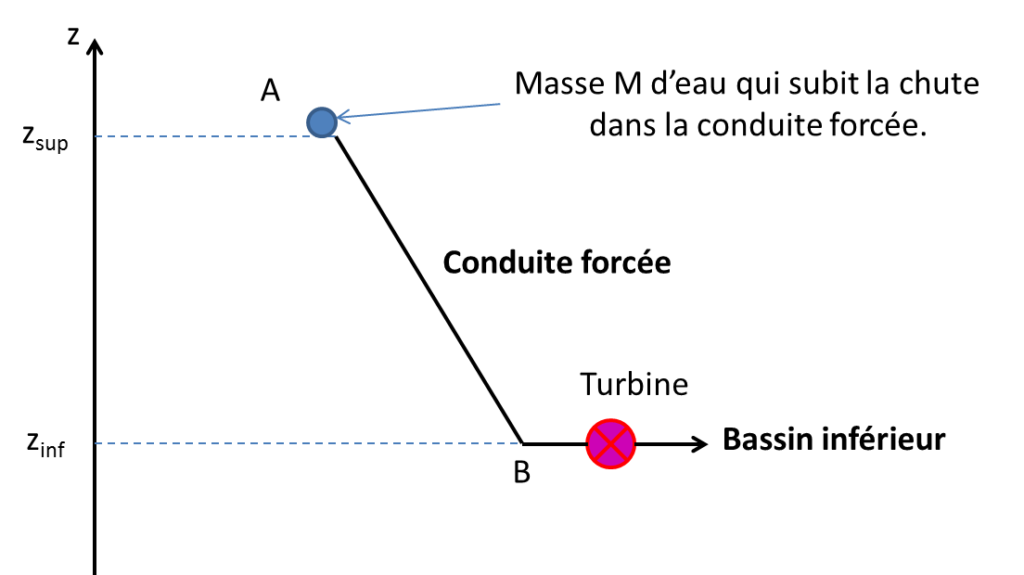
Données :
– altitude du bassin supérieur : zsup = 700 m
– volume du bassin inférieur : Vinf = 150 000 m3
– altitude du bassin inférieur : zinf = 50,0 m
– accélération de la pesanteur : g = 9,81 m.s-2
– masse volumique de l’eau : ρeau = 1000 kg.m-3
– consommation annuelle sur l’île d’El Hierro en 2018 : E = 42,0 GWh
– 1,000 Wh = 3600 J
On se place dans le référentiel terrestre, supposé galiléen, muni d’un axe Oz orienté vers le haut. L’énergie potentielle de pesanteur est prise nulle à l’altitude z = 0.
6. Exprimer la variation de l’énergie potentielle de pesanteur ΔEpp de cette masse M d’eau lors de sa chute à travers la conduite forcée, en fonction de ρeau, Vinf, g, zsup et zinf. Montrer que la valeur de ΔEpp est de l’ordre de − 950 GJ.
$E_{pp}=Mgz$
$\Delta E_{pp}=E_{pp(inférieur)}-E_{pp(supérieur)}$
$\Delta E_{pp}=Mgz_{inf}-Mgz_{sup}$
$\Delta E_{pp}=Mg(z_{inf}-z_{sup})$
Or
$\rho_{eau}=\dfrac{M}{V_{inf}}$
$M=\rho_{eau}\times V_{inf}$
D’ou
$\Delta E_{pp}=\rho_{eau}\times V_{inf}\times g\times(z_{inf}-z_{sup})$
$\Delta E_{pp}=1000\times150\ 000\times9,81\times(50,0-700)$
$\Delta E_{pp}=-9,56.10^{11}\ J$
$\Delta E_{pp}=-956\ GJ$
7. En considérant que l’eau est immobile dans le réservoir supérieur et que la chute à travers la conduite s’effectue sans frottement, déterminer la valeur de l’énergie cinétique de cette masse M d’eau lorsqu’elle actionne les turbines.
En considérant que la chute à travers la conduite s’effectue sans frottement, l’énergie mécanique se conserve :
$\Delta E_m=0$
$\Delta E_c+\Delta E_{pp}=0$
$\Delta E_c=-\Delta E_{pp}$
$E_{c(inférieur)}-E_{c(supérieur)}=-\Delta E_{pp}$
Or l’eau est immobile dans le réservoir supérieur : $E_{c(supérieur)}=0\ J$
$E_{c(inférieur)}=-\Delta E_{pp}$
$E_{c(inférieur)}=956\ GJ$
8. Sachant que le rendement de la phase de turbinage est de 90 %, calculer la valeur de l’énergie électrique que peut fournir la centrale hydro-électrique.
$\eta=\dfrac{E_{electrique}}{E_{c(inférieur)}}$
$E_{electrique}=\eta\times E_{c(inférieur)}$
$E_{electrique}=\dfrac{90}{100}\times956$
$E_{electrique}=860\ GJ$
9. Répondre à la problématique 2 en déterminant le nombre de jours d’autonomie sans vent que représente la réserve d’eau des bassins.
Déterminons le nombre de jours d’autonomie sans vent que représente la réserve d’eau des bassins :
Consommation annuelle sur l’île d’El Hierro en 2018 : $E=42,0\ GWh$
Or $1,000\ Wh=3600\ J$
$42,0\ GWh=42,0\times3600=151200\ GJ$
| Consommation | Nombre de jours |
| $151200\ GJ$ | 1 an = 365 Jours |
| $860\ GJ$ | x |
$$x=\dfrac{860\times365}{151200}=2,08\ jours$$
Problématique 2 : en quoi les infrastructures de l’île de El Hierro lui permettent-elle de s’affranchir des énergies fossiles ?
Ce dispositif permet d’utiliser l’énergie produit par les éoliennes. Concernant le problème d’intermittence (pas de vent), le dispositif de pompage permet d’avoir une réserve d’énergie équivalente à 2 jours de consommations. Ainsi, ce dispositif permet de ne pas utiliser des énergies fossiles.
