Bac Métropole Juin 2021 Sujet 2
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2ME2
Sujet et corrigé
Mots-clés : mouvement dans un champ de pesanteur uniforme ; énergie mécanique
Le saut à l’élastique est un loisir qui permet de ressentir des sensations fortes. Il consiste à sauter dans le « vide » à l’aide d’un élastique attaché aux chevilles. Ce saut peut se faire à partir d’un pont.

Un saut en élastique se déroule en plusieurs phases qui sont décrites ci-dessous.
| 1re phase | 2e phase | 3e phase |
|---|---|---|
 |  |  |
| Chute libre, l’élastique n’est pas tendu. | L’élastique commence à se tendre, le sauteur ralentit. Lorsque l’élastique est complètement étiré, le sauteur s’arrête. | L’élastique se contracte, le sauteur remonte en reprenant de la vitesse puis en ralentissant à nouveau. |
Ces trois phases se répètent jusqu’à ce que le sauteur soit immobile, la durée totale du saut est de l’ordre d’une minute.
L’objectif de cet exercice est d’évaluer la vitesse du sauteur à la fin de la 1re phase et la longueur maximale du saut.
On étudie un saut réalisé à partir d’un pont situé à une hauteur H d’environ 50 m au-dessus du sol.
Données :
- masse de la personne avec l’équipement : m = 80 kg ;
- valeur du champ de pesanteur terrestre : g = 9,81 m·s–2 ;
- longueur de l’élastique non étiré : L0 = 8,0 m.
Lors de la 1re phase du saut à l’élastique, on étudie le mouvement du sauteur dont le centre de masse est noté S, dans le cadre du modèle de la chute libre.
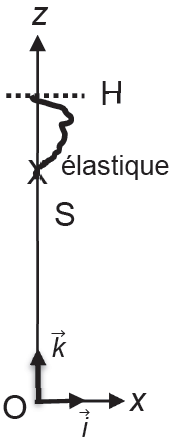
Pour simplifier, on suppose que le mouvement est vertical.
À la date t = 0, la personne démarre le saut à la hauteur H avec une vitesse initiale dont le vecteur $\overrightarrow{v_0}$ est vertical et dirigé vers le bas et de norme v0.
Le référentiel d’étude est le référentiel terrestre supposé galiléen muni du repère d’espace (Ox ; Oz) dont l’origine O du repère est au niveau du sol. L’axe (Oz) est vertical, dirigé vers le haut et muni du vecteur unitaire $\overrightarrow{k}$ . La situation est schématisée ci-contre.
1. Déterminer les coordonnées du vecteur accélération $\overrightarrow{a}(t)$ de S dans le repère (Ox ; Oz).
Réponse :
Système {sauteur}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$\sum_{}^{}\overrightarrow{F}_{ext}=m\overrightarrow{a}$
$\overrightarrow{P}=m\overrightarrow{a}$
$m\overrightarrow{g}=m\overrightarrow{a}$
$\overrightarrow{a}=\overrightarrow{g}$
Or
$\overrightarrow{g} \begin{cases} 0 \\-g \end{cases}$
$\overrightarrow{a} \begin{cases} a_{x}(t)=0 \\a_{z}(t)=-g \end{cases}$
2. Établir que l’équation horaire du mouvement selon l’axe Oz s’écrit :
$z(t)= – \frac{1}{2}g \cdot t^2- v_0 \cdot t+H $
Réponse :
$\overrightarrow{a}=\frac{d \overrightarrow{v}}{dt}$
On intègre le système d’équation précédent :
$\overrightarrow{v} \begin{cases} v_{x}(t)=C_{1} \\v_{z}(t)=-gt+C_{2}\end{cases}$
Pour trouver les constantes, on utilise $\overrightarrow{v_0}$ :
$\overrightarrow{v} \begin{cases} v_{0x}=0\\v_{0z}=-v_{0}\end{cases}$
d’ou
$\overrightarrow{v} \begin{cases} v_{x}(t)=0 \\v_{z}(t)=-gt-v_{0}\end{cases}$
$\overrightarrow{v}=\frac{d \overrightarrow{OM}}{dt}$
On intègre le système d’équation précédent :
$\overrightarrow{OM} \begin{cases} x(t)=C_{3} \\z(t)=-\frac{1}{2}gt^2-v_{0}\times t + C_{4}\end{cases}$
Pour trouver les constantes, on utilise $\overrightarrow{OM}_0$
$\overrightarrow{OM}_0 \begin{cases} x_0=0 \\z_0=H\end{cases}$
d’ou
$\overrightarrow{OM} \begin{cases} x(t)=0 \\z(t)=-\frac{1}{2}gt^2-v_{0}\times t + H \end{cases}$
3. Après traitement de la vidéo d’un saut à l’aide d’un logiciel de pointage et modélisation des résultats, on obtient l’équation horaire suivante :
z(t) = – 4,90 t2 – 1,10 t + 49,8 avec z exprimé en m et t exprimé en s.
La modélisation des résultats expérimentaux est-elle cohérente avec l’expression donnée en 2. ? Justifier à l’aide de deux arguments.
$$z\left(t\right)=-\frac{1}{2}gt^2-v_0t+H$$
$$z\left(t\right)=-4,90\ t^2-1,10\ t+49,8$$
Par identification :
$$-\frac{1}{2}g=-4,90$$
$$g=-4,90 \times -2$$
$$g=9,80\ m{.s}^{-2}$$
C’est cohérent avec la valeur de g.
Par identification :
H=49,8m
C’est cohérent avec la valeur de H donné par l’énoncé H environ 50 m.
4. Calculer la date à laquelle l’élastique commence à se tendre.
Date à laquelle l’élastique commence à se tendre : temps à partir duquel L>L0.
$$z=H-L_0=49,8-8=41,8$$
$$z=-4,90t^2-1,10t+49,8$$
$$41,8=-4,90t^2-1,10t+49,8$$
$$0=-4,90t^2-1,10t+8,0$$
$$0=-4,90t^2-1,10t+8,0$$
Résolvons cette équation du second degré :
$$
\Delta = b^2 – 4ac
$$
$$
\Delta = (-1,10)^2 – 4 \times (-4,90) \times 8
$$
$$
\Delta = 158
$$
$$
t_1 = \frac{-b + \sqrt{\Delta}}{2a}
$$
$$
t_1 = \frac{-(-1,10) + \sqrt{158}}{2 \times -4,90} = -1,39\ \text{s}
$$
$$
t_2 = \frac{-b – \sqrt{\Delta}}{2a}
$$
$$
t_2 = \frac{-(-1,10) – \sqrt{158}}{2 \times -4,90} = 1,17\ \text{s}
$$
On garde la valeur positive du temps : t=1,17 s
5. En déduire la valeur de la vitesse atteinte à cet instant.
$$v_{(t=1,17\ )}=\sqrt{v_x^2+v_z^2}$$
$$v_{(t=1,17\ )}=\sqrt{0^2+{(-gt-v_0)}^2}$$
$$v_{(t=1,17\ )}=\sqrt{{(-9,8 \times 1,17-1,1)}^2}$$
$$v_{(t=1,17\ )}=12,6\ m.s^{-1}$$
6. Distance de sécurité
Lors du saut, les différentes énergies intervenant au cours du mouvement ont été calculées à l’aide des informations fournies sur la vidéo du saut. Elles ont été représentées dans la figure 1. L’énergie potentielle de pesanteur est considérée nulle quand z = 0.
Pour une des énergies, les calculs n’ont pu être effectués que sur la 1ère phase du saut (courbe A).
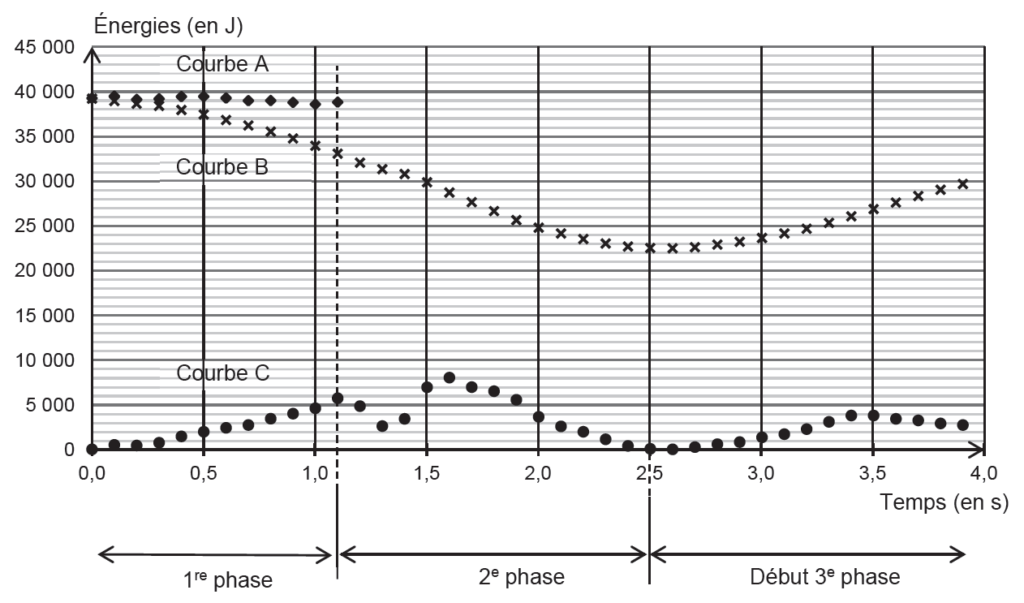
6.1. Identifier parmi les courbes A, B, C de la figure 1 celle représentant l’énergie cinétique, celle représentant l’énergie potentielle de pesanteur et celle représentant l’énergie mécanique. Justifier ces choix.
L’énergie cinétique est définie par : $E_c=\frac{1}{2}m.v^2$
L’énergie potentielle de pesanteur d’un solide est: Epp=mgz
L’énergie mécanique Em d’un système est la somme des énergies cinétique et potentielle : EM=EC+Ep
La courbe A est au-dessus des autres, c’est l’énergie mécanique
La courbe B est l’énergie potentielle car au début le sauteur a une grande altitude donc une grande énergie potentielle.
La courbe C est l’énergie cinétique car au début le sauteur n’a pas de vitesse, l’énergie cinétique est nulle au début (bien que dans la partie précédente, la vitesse initiale n’est pas nulle).
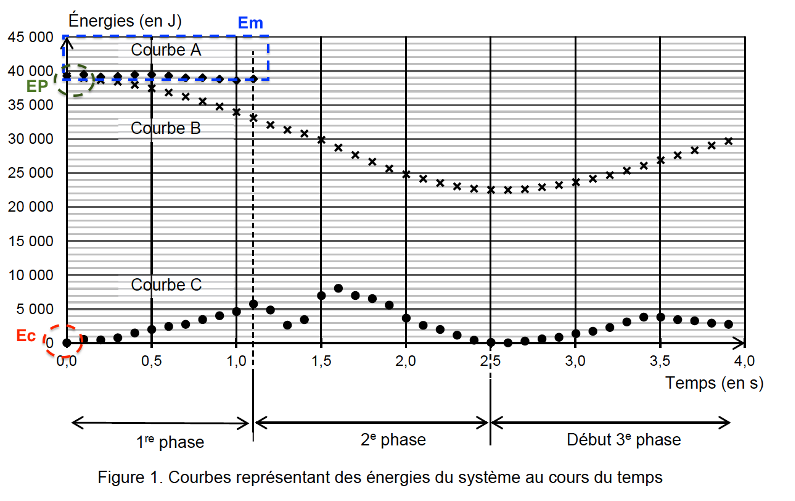
6.2. Identifier l’(les) information(s) manquante(s) sur le système physique étudié nécessaire au tracé de la suite de la courbe A pour les deuxième et troisième phases.
Élastique tendu emmagasine de l’énergie potentielle élastique.
6.3. Pour des raisons de sécurité, il est nécessaire que l’élastique soit choisi tel que son étirement ∆L soit inférieur ou égal à 4 L0. À l’aide de la figure 1, calculer la distance maximale parcourue par le sauteur. Conclure.
Distance maximale parcourue par le sauteur : on regarde ${\rm Epp}_{min}=22500\ J$
Or
$${\rm Epp}_{min}=mgz_{min}$$
$$z_{min}=\frac{{\rm Epp}_{min}}{mg}$$
$$z_{min}=\frac{22500}{80 \times 9,8}=28,7\ m$$
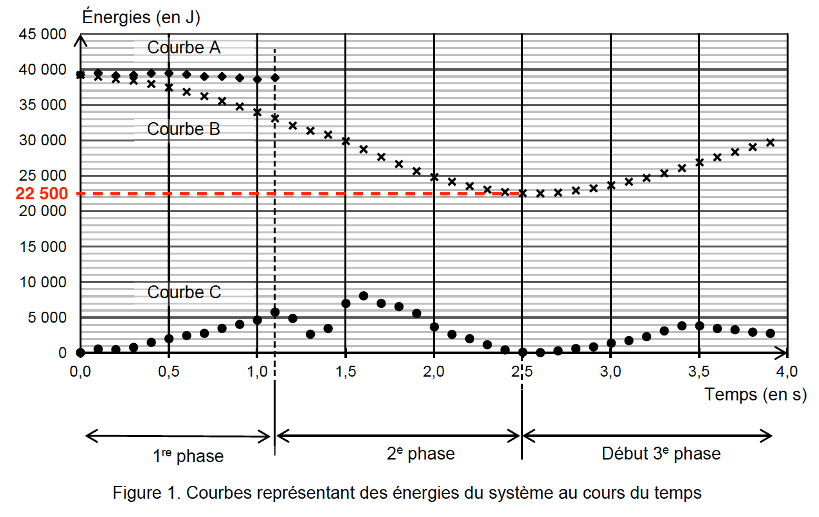
$$
\Delta L = H – z_{min}
$$
$$
\Delta L = 50 – 28,7 = 21,3\ \text{m}
$$
Comparons ∆L et L0 :
$$
\frac{\Delta L}{L_0} = \frac{21,3}{8,0} = 2,7
$$
$$
\Delta L = 2,7\,L_0 < 4\,L_0
$$
La sécurité du sauteur est donc assurée.
