Seul sur Mars

Enseignement scientifique première

Durée 1h – 10 points – Thème « Le Soleil, notre source d’énergie »

En 2035, lors d’une expédition de la mission Ares III sur Mars, l’astronaute Mark Watney est laissé pour mort par ses coéquipiers, une tempête les ayant obligés à décoller de la planète en urgence.

Le lendemain, Mark Watney, qui n’est que blessé, se réveille et découvre qu’il est seul sur Mars.

Pour survivre, il décide de cultiver des pommes de terre sous le dôme de la base, en utilisant le sol martien fertilisé avec les excréments de l’équipage, de l’eau et l’énergie solaire.

Source : http://www.allocine.fr/film/fichefilm-221524/dvd-blu-ray/?cproduct=443240

Partie 1. Puissance rayonnée par le Soleil

Le Soleil, d’une masse totale de 2,0×10³⁰ kg, est l’étoile du système solaire. Il est composé majoritairement d’atomes d’hydrogène H et d’atomes d’hélium He. Autour de lui gravitent la Terre et d’autres planètes comme Mars. La puissance rayonnée par le Soleil est voisine de 3,9×10²⁶ W.

Document 1. Réaction nucléaire de synthèse de l’hélium à partir de l’hydrogène dans le Soleil

Sous l’effet de la température suffisamment élevée existant au cœur du Soleil, quatre noyaux d’hydrogène peuvent réagir pour former un noyau d’hélium et deux positons selon l’équation de la réaction nucléaire simplifiée, dans laquelle ⁰₁e représente un positon (particule de charge opposée à celle de l’électron) :

$4{}^{1}_{1}H \rightarrow {}^{4}_{2}He+2{}^{0}_{1}e$

Cette réaction s’accompagne d’une perte de masse et donc d’un dégagement d’énergie.

1 – Indiquer en le justifiant, si la formation de l’hélium dans le Soleil est une réaction de fusion ou de fission nucléaire.

La formation de l’hélium dans le Soleil consiste à fusionner 4 atomes d’hydrogène pour former un noyau d’hélium : c’est une réaction de fusion nucléaire.

Partie 2. Puissance solaire reçue par Mars

La base martienne de la mission Ares III est alimentée en énergie par des panneaux solaires qui captent le rayonnement solaire arrivant sur le sol martien. On souhaite connaître la puissance reçue par ces panneaux solaires.

2 – Sachant que la planète Mars est située à la distance d_M-S = 2,3×10⁸ km du Soleil, et à partir des données de la partie 1, calculer en W·m^-2 la puissance par unité de surface traversant la sphère dont le centre est le Soleil et dont le rayon est d_M-S. Cette puissance par unité de surface appelée constante solaire de Mars et notée C_Mars.

Donnée : aire S d’une sphère de rayon d : S = 4×π×d².

Puissance par unité de surface

$C_{Mars}=\frac{P}{S}$

$C_{Mars}=\frac{P}{4\times \pi \times d_{M-S}^2}$

$C_{Mars}=\frac{3,9 \times 10^{26}}{4\times \pi \times (2,3\times 10^{8}\times 10^{3})^2}$

C_Mars=587 W.m^-2

Document 2. Schéma d’un disque recevant une puissance solaire égale à celle reçue par Mars

La puissance solaire reçue par Mars traverse un disque fictif de rayon R_Mars et se répartit ensuite sur toute la surface de la sphère martienne de rayon R_Mars. Celle-ci est en rotation sur elle-même.

On peut considérer que le disque fictif est situé à la même distance du Soleil que Mars.

Source : Daujean, C. D., & Guilleray, F. G. (2019). Le bilan radiatif terrestre. Éd. Hatier, Enseignement scientifique (p. 101).

3 – La puissance solaire moyenne reçue sur Mars par unité de surface est proche de C_Mars/4 ; sa valeur est voisine de 150 W·m^-2. Expliquer qualitativement pourquoi cette puissance moyenne par unité de surface est plus petite que C_Mars.

Aire du disque :

$S_{disque}=\pi \times R_{Mars}^2$

Aire d’une sphère:

$S_{sphère}=4\times \pi \times R_{Mars}^2$

$\frac{S_{sphère}}{S_{disque}}=\frac{4\times \pi \times R_{Mars}^2}{\pi \times R_{Mars}^2}=4$

$S_{sphère}=4\times S_{disque}$

La puissance solaire reçue par Mars traverse un disque fictif de rayon R_Mars et se répartit ensuite sur toute la surface de la sphère martienne de rayon R_Mars. Or la surface de la sphère est 4 fois plus grande que la surface du disque. Ainsi La puissance solaire moyenne reçue sur Mars par unité de surface est proche de C_Mars/4

Partie 3. Des pommes de terre sur Mars

Le dôme de la base martienne permet de recréer l’atmosphère terrestre. Grâce à un ingénieux système permettant de fournir l’eau nécessaire à la croissance des végétaux et à un éclairage adapté alimenté en électricité par les panneaux solaires, Mark Watney, botaniste de formation, décide de réaliser une culture végétale qui lui fournira de la nourriture nécessaire à sa survie.

4 – À partir de l’exploitation des résultats expérimentaux du document 3 ci-après, identifier un facteur essentiel à la production de glucides par la plante.

Sur le document 3, nous remarquons que le CO₂ ne se transforme en glucide dans la plante que dans la partie éclairée.

Le facteur essentiel à la production de glucides par la plante est la lumière.

Document 3. Fixation du CO2 par une feuille

Une feuille est mise au contact en son centre avec du CO₂ marqué au ¹⁴C radioactif durant 5 minutes. Le CO₂ marqué peut diffuser dans la feuille à partir de la zone centrale. Seule la moitié de la feuille est exposée à la lumière. La technique d’autoradiographie permet de localiser des sucres radioactifs qui impressionnent fortement une plaque photographique mise au contact de la feuille (zone sombre sur le document).

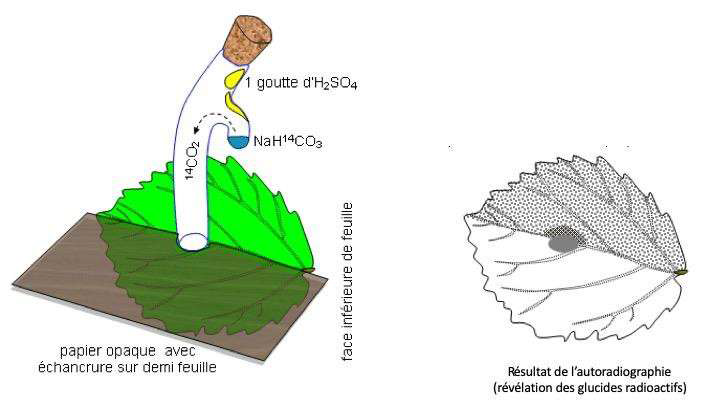
D’après : http://svt.ac-dijon.fr/schemassvt/IMG/gif/co2_feuill_maz.gif

5 – Au 79^ème jour, Mark Watney récolte les tubercules de pomme de terre, qui ont stocké de l’énergie sous forme chimique.

Calculer le nombre de jours d’autonomie dont dispose Mark Watney grâce à sa récolte de pommes de terre avant qu’une nouvelle mission ne vienne le récupérer sur Mars.

Expliciter la démarche.

Données :

Surface du champ de pommes de terre : S = 126 m²
Rendement* de la pomme de terre : r = 3 kg·m^-2
Apport énergétique des pommes de terre : A = 3400 kJ·kg^-1
Dépense énergétique moyenne par sol martien de Mark Watney : D = 11000 kJ

* En agriculture, on appelle rendement la masse végétale récoltée par unité de surface et par saison.

Calculons la masse de pommes de terre cultivée :

r=m/S

m/S=r

m=r×S

m=3×126

m=378 kg

Calculons l’énergie chimique disponible dans ces pommes de terre :

A=E/m

E/m=A

E=A×m

E=3400×378

E=1 285 200 KJ

Calculons le nombre de jours d’autonomie dont dispose Mark Watney grâce à sa récolte de pommes de terre avant qu’une nouvelle mission ne vienne le récupérer sur Mars :

1 jour	D=11 000 KJ
N jours	E=1 285 200 KJ

N=(E×1)/D

N=(1 285 200 ×1)/(11 000)

N=117 jours

Mark Watney dispose de 117 jours d’autonomie grâce à sa récolte de pommes de terre avant qu’une nouvelle mission ne vienne le récupérer sur Mars.