Enseignement scientifique première
Durée 1h – 10 points – Thème « La Terre, un astre singulier »
Anaxagore (v. -500 ; -428) et Ératosthène (v. -276; v. -194) sont deux mathématiciens qui se sont intéressés à la forme de la Terre : Anaxagore pensait qu’elle était plate alors qu’Ératosthène pensait qu’elle était sphérique.
Document 1 : Anaxagore
Anaxagore est un philosophe grec qui s’est intéressé aux mathématiques et à l’astronomie. Il a l’intuition, par exemple, que la Lune brille en réfléchissant les rayons du Soleil et fournit une explication valable des éclipses lunaires et solaires. Il pense, d’autre part, que la Terre est un disque plat et, sous cette hypothèse, il cherche à calculer la distance de la Terre au Soleil.
Il a appris par des voyageurs venant de la ville de Syène (S) que, lors du solstice d’été, le Soleil (H) est au zénith à midi et donc que les objets n’ont pas d’ombre à ce moment précis. Au même moment, quelques 800 km plus au nord, à l’emplacement de ce qui deviendra la ville d’Alexandrie (A), le soleil éclaire un puits de 2 m de diamètre jusqu’à une profondeur de 16 m.
La figure 1 représente la situation à midi lors du solstice d’été.
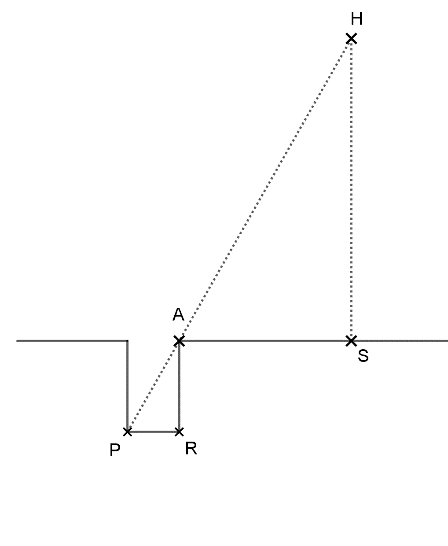
1 – Compléter le schéma de l’annexe avec les informations chiffrées du document 1.
Quelle longueur de ce schéma Anaxagore cherche-t-il à calculer ?
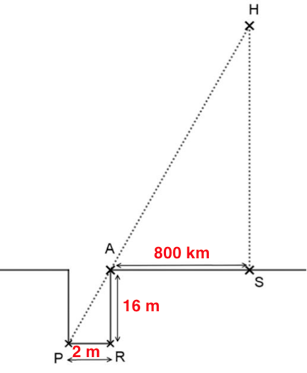
Il cherche à calculer la distance de la Terre au Soleil : SH
2 – Calculer la distance Terre-Soleil dans le modèle d’Anaxagore.
Calculons la distance Terre-Soleil dans le modèle d’Anaxagore :
Le triangle ASH est perpendiculaire en S et le triangle APR est perpendiculaire en R. Ils possèdent un angle droit.
De plus, les points PAH sont alignés et les droites AS et PR sont parallèles. Ainsi les angles (APR) et (HAS) sont égaux.
Ainsi les triangles ASH et APR sont semblables.
Les longueurs de leurs côtés sont donc proportionnelles.
![\[\frac{AP}{AH} =\frac{PR}{AS}=\frac{AR}{SH} \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-b987a4189bd6fa889902cd78d34b50d3_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{16}{AH} =\frac{2}{800000}=\frac{16}{SH} \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-f94f1bd9d74abc91cb6cfad763d06382_l3.png "Rendered by QuickLaTeX.com")
Distance Terre-Soleil : SH
![\[\frac{2}{800000}=\frac{16}{SH} \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-2d299adba8b298a1eddf891dc3198964_l3.png "Rendered by QuickLaTeX.com")
![\[SH=\frac{800000 \times 16}{2} \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-edebbd443fc9e72c0532d991cd2a4e29_l3.png "Rendered by QuickLaTeX.com")
SH=6 400 000 m
SH=6 400 km
3 – On estime aujourd’hui que la distance moyenne Terre-Soleil est de 150 millions de kilomètres soit 25000 fois plus. Expliquer pourquoi la valeur trouvée par Anaxagore est très éloignée de la valeur réelle.
La valeur trouvée par Anaxagore 6400 km est très éloignée de la valeur réelle 150 millions de kilomètres soit 25000 fois plus.
L’erreur que fait Anaxagore est de considérer la terre plate. De plus, le soleil étant très éloigné, ses rayons arrivent parallèles entre eux.
Document 2 : Eratosthène
Eratosthène, autre philosophe grec intéressé lui aussi par les mathématiques et la forme de la Terre, considère que la Terre est sphérique et il cherche à calculer son rayon.
Il connaît lui aussi la distance de 800 km entre Syène (S) et Alexandrie (A) et sait qu’à midi, lors du solstice d’été, le soleil est au zénith à Syène. Il fait une hypothèse importante pour son modèle : il pense que le soleil est très éloigné de la Terre et que, par conséquent, ses rayons sont parallèles en arrivant sur la Terre.
Il utilise un instrument de mesure qui lui permet de trouver un angle d’un cinquantième de tour, soit 7,2°, entre les rayons du soleil et la verticale à Alexandrie.
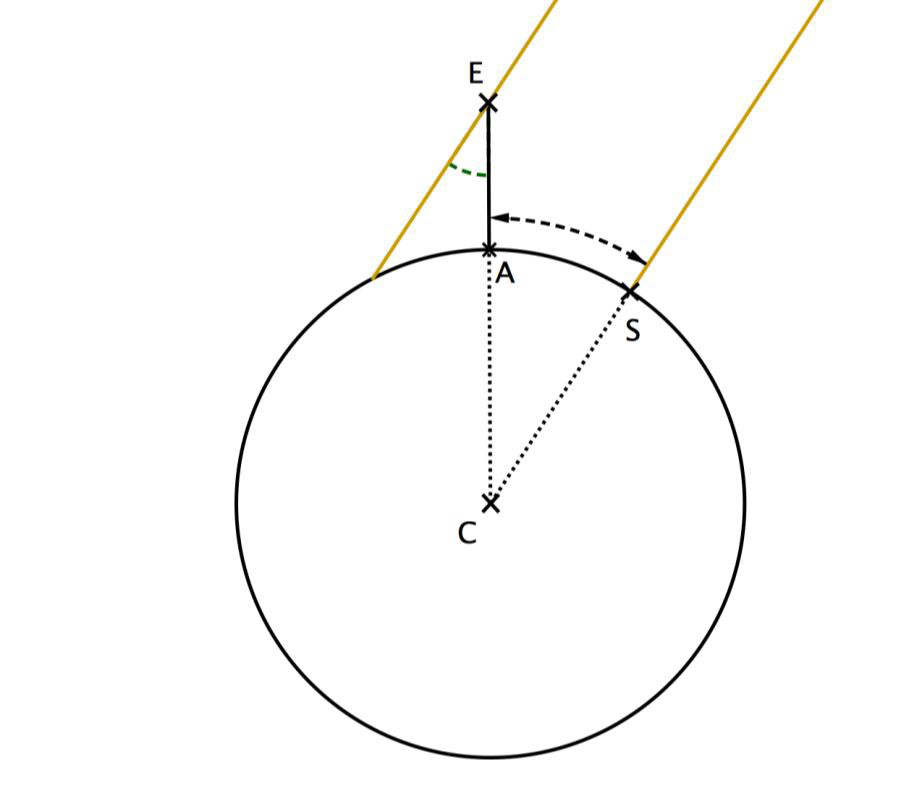
La figure 2 représente la situation à midi lors du solstice d’été. Le segment [EA] représente la verticale à Alexandrie et C le centre de la Terre.
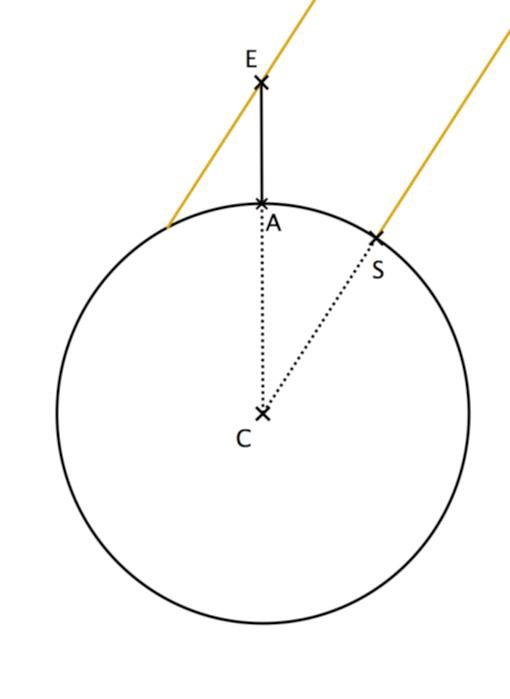
4 – Compléter le schéma de l’annexe avec les informations chiffrées du texte du document 2.
Quelle longueur de ce schéma Ératosthène cherche-t-il à calculer ?
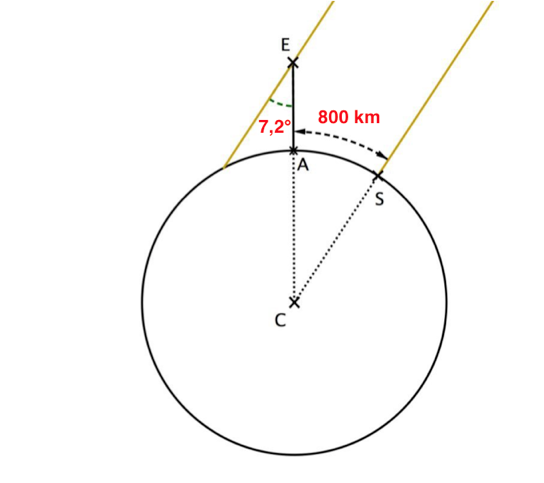
Ératosthène cherche à calculer longueur CA ou CS de ce schéma qui correspondent au rayon de la terre.
5 – Déterminer la mesure de l’angle ACS^. Justifier la réponse en s’appuyant sur des propriétés géométriques.
Calculer la circonférence de la Terre puis en déduire le rayon de la Terre au kilomètre près.
Les rayons du soleil sont parallèles entre eux. EC est une droite qui coupe ces deux droites parallèles.
Les angles E ̂ et (ACS) ̂ sont alternes internent et sont donc de même valeur. (ACS) ̂=E ̂=7,2°
Calculons la circonférence de la Terre :
| AS=800 km | 7,2° |
| circonférence | 360° |
circonférence=(360×800)/7,2
circonférence=40 000 km
Calculons le rayon de la Terre au kilomètre près.
circonférence=2π×r
2π×r=circonférence
r=circonférence/2π
r=(40 000 )/2π
r=6366 km
6 – On estime aujourd’hui que le rayon de la Terre est de 6371 km. Calculer l’erreur en pourcentage commise par Ératosthène. Commenter.
Calculons l’erreur en pourcentage commise par Ératosthène
![\[\textrm{erreur en pourcentage}=\frac{6371-6366}{6371} \]](https://physik.fr/wp-content/ql-cache/quicklatex.com-332ff6715516179f2c5f4c050449013e_l3.png "Rendered by QuickLaTeX.com")
erreur en pourcentage=0,00078
erreur en pourcentage=0,078%
L’erreur en pourcentage commise par Ératosthène est très faible. Le résultat trouvé est très précis. C’est remarquable de trouver un résultat si précis pour son époque.
Document réponse à rendre avec la copie
La forme de la Terre
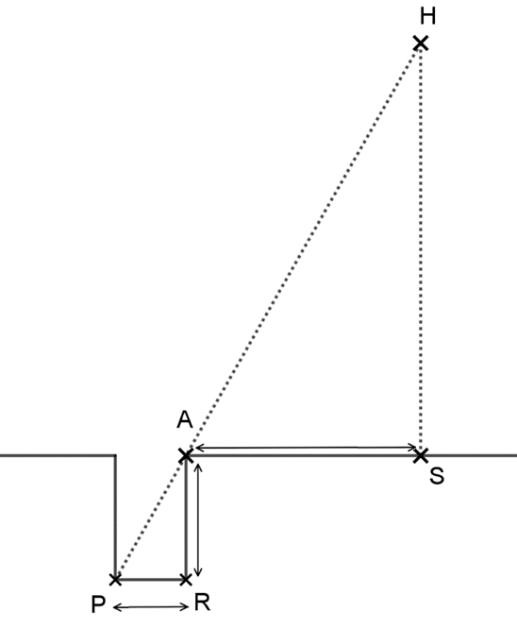
Question 1
H représente le Soleil, S la ville de Syène, A la ville d’Alexandrie et le segment [𝑃𝑅] le fond du puit. Le schéma n’est pas à l’échelle.
Question 4
C représente le centre de la Terre, S la ville de Syène, A la ville d’Alexandrie et le segment [𝐸𝐴] la verticale à Alexandrie. Le schéma n’est pas à l’échelle.
