Tissage d’une voile de bateau

Bac Asie 2024 Sujet 2

Exercice 1 – (11 points) –  Durée 1h56 – Calculatrice autorisée

Sujet n°24-PYCJ2JA1

Exercice 1 – Tissage d’une voile de bateau (11 points)

Jusqu’à récemment, les voiles des voiliers étaient réalisées à l’aide d’un tissage de fils de nylon. Toutefois, depuis une décennie, de nouveaux matériaux composites plus performants (kevlar, carbone) sont utilisés pour concevoir les fils. De plus, ils peuvent être tissés de façon plus ou moins serrée en fonction des contraintes auxquelles sont soumis les différents secteurs de la voile.

L’objet de cet exercice est d’étudier la possibilité de distinguer ces tissages. L’observation directe, à l’œil nu et avec l’aide d’une loupe, est étudiée dans une première partie. Une seconde partie est consacrée à l’exploitation du phénomène d’interférence.

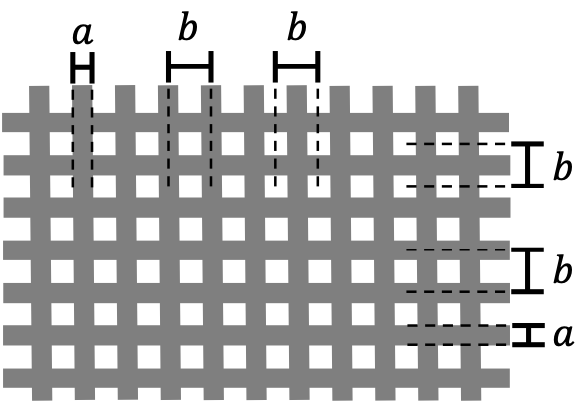
L’objet d’étude est une voile réalisée avec des fils de carbone. Le tissage est représenté dans le document 1. Il est caractérisé par deux paramètres principaux :

• Le diamètre des fils noté 𝑎.
• L’espacement entre les fils noté 𝑏. Il correspond également à l’espacement entre les vides et est supposé identique dans les deux directions du tissage.

Document 1 – Caractéristiques du tissage

Partie 1 – Observation directe

Dans un premier temps, on cherche à observer le tissage à l’œil nu. On se donne comme critère d’observation de pouvoir distinguer l’épaisseur des fils de diamètre 𝑎.

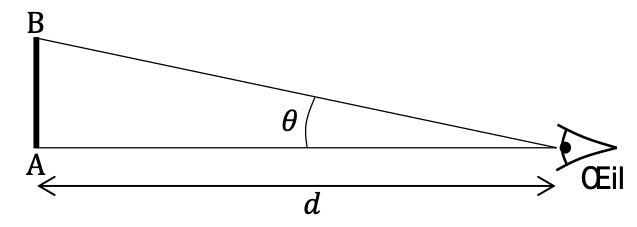
La capacité de l’œil à distinguer un objet dépend du « champ angulaire » qu’il occupe dans le champ de vision. Le champ angulaire, noté 𝜃 dans la suite, est défini comme l’angle entre les rayons issus des bords de l’objet observé lorsqu’ils atteignent le centre de la pupille (voir document 2, page 3).

Le pouvoir séparateur de l’œil, noté 𝜀, correspond au champ angulaire minimal que doit occuper un objet pour qu’il puisse être distingué. Autrement dit :

• Si 𝜃 > 𝜀 : l’objet peut être distingué ; ses extrémités sont perçues comme des points distincts.
• Si 𝜃 < 𝜀 : l’objet ne peut pas être distingué ; il est perçu comme un point unique.

Pour augmenter les chances de distinguer un objet, il faut l’observer sous le plus grand champ angulaire possible. Pour cela, on peut se rapprocher de l’objet. Toutefois, l’œil a une limite dans sa capacité à voir nettement des objets proches. En notant 𝑑 la distance entre l’objet observé et l’œil (voir document 2, page 3), on estime que la plupart des gens ne peuvent pas voir nettement un objet situé à une distance inférieure à 𝑑_m = 0,25 m.

Document 2 – Observation d’un objet : champ angulaire, distance d’observation

Dans toute cette partie, on considère que les angles étudiés sont toujours très faibles. On peut donc utiliser l’approximation des petits angles :

tan 𝜃 ≈ 𝜃 (avec 𝜃 en radian)

On considère un observateur qui regarde la toile de la voile à la distance 𝑑_m. Il cherche à distinguer l’épaisseur des fils, caractérisée par leur diamètre 𝑎 = 10 μm. On note 𝜃_𝑎 le champ angulaire correspondant à l’épaisseur d’un fil.

Q1- Exprimer le champ angulaire 𝜃_𝑎 en fonction de 𝑎 et 𝑑_m.

Q2- Évaluer 𝜃_𝑎.

$\theta_a=\frac{a}{d_m}$
$\theta_a=\frac{10\times{10}^{-6}}{0,25}$
$\theta_a=4,0\times{10}^{-5}\ \text{rad}$

Q3- Justifier que l’observateur ne peut pas distinguer l’épaisseur des fils à l’œil nu.

Pouvoir séparateur : $\varepsilon = 3,0\times{10}^{-4}\ \text{rad}$
$\theta_a<\varepsilon$ ; l’angle est inférieur au pouvoir séparateur : l’observateur ne peut pas distinguer l’épaisseur des fils à l’œil nu.

Pour surmonter cette difficulté, l’observateur décide de s’aider d’une loupe. Une loupe est un système optique constitué d’une unique lentille convergente. On l’utilise pour « grossir » des objets de petite taille, ce qui signifie que la loupe permet de produire des images occupant un champ angulaire plus grand que celui occupé par l’objet.

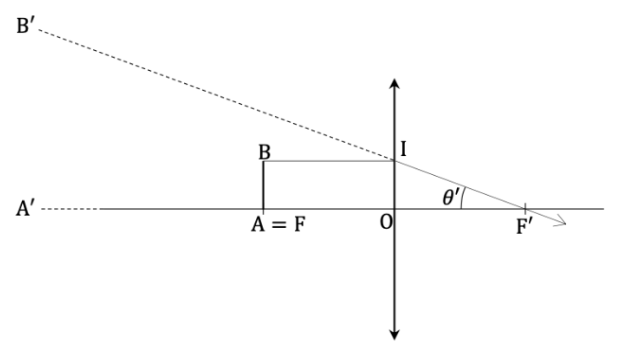
Document 3 – Formation d’une image à l’infini au travers d’une loupe

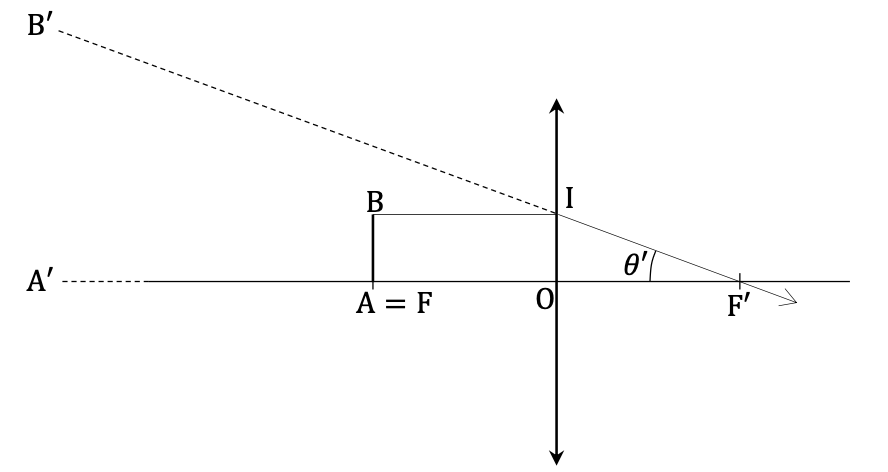
Le point I est un point de construction représenté pour aider à l’analyse de la figure.

Pour utiliser une loupe, on place l’objet AB au voisinage du foyer objet F de la lentille. L’image A′B′ se forme alors à l’infini. Les points A′ et B^′ étant à l’infini, le champ angulaire 𝜃′ associé à l’image 𝐴′𝐵′ est le même quelle que soit la position de l’œil de l’observateur. On peut donc caractériser 𝜃′ en étudiant la configuration des rayons au foyer image, tel que représenté sur la figure du document 3, page 3.

L’observateur souhaite observer le tissage avec la loupe. Il dispose de trois loupes de focales respectives : 12,5 cm ; 5,0 cm ; 2,5 cm.

Q4- À l’aide du document 3, page 3, montrer que le champ angulaire 𝜃_𝑎′ sous lequel l’observateur voit un fil de diamètre 𝑎 à travers la loupe est relié la distance focale 𝑓′ de la lentille par la relation :

$$\theta’_a=\frac{a}{f’}$$

Q5- En déduire que l’observateur peut distinguer l’épaisseur des fils lorsque :

$$f'<\frac{a}{\varepsilon}$$

Pour que l’observateur puisse distinguer l’épaisseur des fils, il faut que
${\theta\prime}_a>\varepsilon$

D’où
$\frac{a}{f\prime}>\varepsilon$
$\frac{f\prime}{a}<\frac{1}{\varepsilon}$
$f\prime<\frac{a}{\varepsilon}$

Q6- Indiquer, en justifiant, la ou les loupes qui permettent de distinguer l’épaisseur des fils.

$f\prime<\frac{a}{\varepsilon}$
$f\prime<\frac{10\times{10}^{-6}}{3,0\times{10}^{-4}}$
$f\prime<3,3\times{10}^{-2}\ \text{m}$
$f\prime<3,3\ \text{cm}$

Ainsi, pour distinguer l’épaisseur des fils, il faut que la distance focale de la lentille utilisée soit inférieure à 3,3 cm.

Une seule lentille respecte cette condition, celle de distance focale 2,5 cm.

Partie 2 – Analyse par interférences

L’observation à la loupe peut permettre de distinguer les fils. Toutefois, elle ne permet pas une caractérisation précise du tissage, c’est-à-dire une évaluation de l’espacement 𝑏 entre les fils. Pour caractériser plus finement cet espacement, on envisage une autre méthode : les interférences optiques avec un laser.

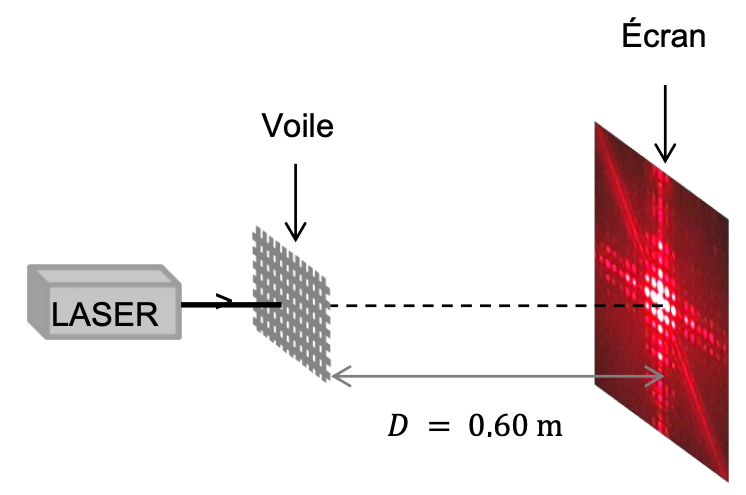
Le principe est le suivant : on tend la partie de voile que l’on souhaite étudier et on l’éclaire par un laser en incidence normale. Sur un écran parallèle à la voile et placé à une distance

𝐷 en arrière de celle-ci, on obtient une figure d’interférences. Le document 4 représente le montage réalisé avec un aperçu de la figure obtenue.

Document 4 – Montage utilisé pour l’analyse par interférences

Étude des fentes d’Young

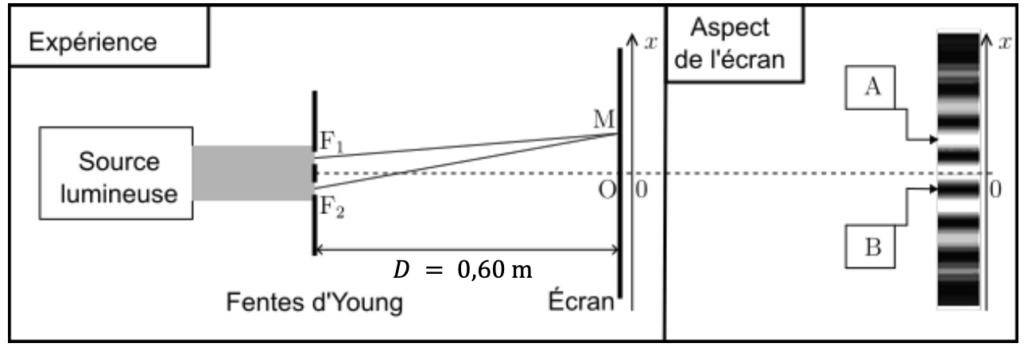
Pour interpréter la figure obtenue, on peut s’appuyer sur le cas plus simple des interférences par deux fentes (fentes d’Young). Le montage de l’expérience des fentes d’Young est très voisin de celui décrit dans le document 4, page 4. La seule différence est que l’on remplace la voile par un écran percé de deux fentes. Comme pour le tissage de la voile, on note 𝑏 la distance entre les deux fentes (𝑏 = F₁F₂ sur la figure du document 5).

Le phénomène d’interférence est directement lié à la différence de chemin optique 𝛿 entre les rayons issus de F₁ et F₂ lorsqu’ils se rencontrent en un point M de l’écran. Le document 5 rassemble ces informations et montre la figure d’interférences obtenue.

Document 5 – Montage des fentes d’Young

La source lumineuse est un laser de longueur d’onde 𝜆.

Dans une situation d’interférences, on distingue deux situations extrêmes : les interférences constructives et les interférences destructives.

Q7- Indiquer, en justifiant, la nature des interférences (constructives ou destructives) aux points A et B repérés sur la figure du document 5.

Au point A on observe une zone brillante, l’interférence y est donc constructive.
Au point B on observe une zone sombre, l’interférence y est donc destructive.

Pour exploiter la figure d’interférences, il faut la caractériser en utilisant le concept d’interfrange dont la valeur est liée à l’espacement 𝑏. Ainsi, on peut déduire une mesure de 𝑏 à partir de la mesure de l’interfrange noté 𝑖.

Pour mener cette démarche, il est nécessaire de connaître l’expression de la différence de chemin optique. Dans la situation de l’expérience décrite, on peut montrer que la différence de chemin optique 𝛿(𝑀) au point M de l’écran a pour expression :

$$\delta(M)=\frac{b}{D}x$$

Dans cette expression, 𝑥 est l’abscisse du point M sur l’écran, l’origine étant au point O.

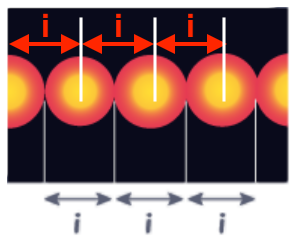
Q8- Rappeler la définition de l’interfrange 𝑖 et l’illustrer par un schéma.

Q9- Rappeler la condition sur la différence de chemin optique pour observer des interférences constructives.

Pour observer des interférences constructives, il faut que : $\delta=k\times\lambda$.

Q10- Montrer que la relation liant l’interfrange 𝑖 et l’espacement 𝑏 est :

$$i=\frac{D}{b}\lambda$$

D’après l’énoncé :
$\delta\left(M\right)=\frac{b}{D}x$
$\frac{b}{D}x=\delta\left(M\right)$
$x=\delta\left(M\right)\times\frac{D}{b}$

Pour des interférences constructives, il faut que :
$\delta=k\times\lambda$

Ainsi, pour des interférences constructives :
$x=k\times\lambda\times\frac{D}{b}$

L’interfrange est la distance entre le centre de deux franges brillantes consécutives ou deux franges sombres consécutives.
Ainsi :
$i=x\left(k+1\right)-x\left(k\right)$

$i=\frac{\left(k+1\right)\times\lambda\times D}{b}-\frac{k\times\lambda\times D}{b}$
$i=\frac{\left(k+1\right)\times\lambda\times D-k\times\lambda\times D}{b}$
$i=\frac{k\times\lambda\times D+1\times\lambda\times D-k\times\lambda\times D}{b}$
$i=\frac{1\times\lambda\times D}{b}$

$i=\frac{\lambda\times D}{b}$
$i=\frac{D}{b}\lambda$

Retour sur la voile

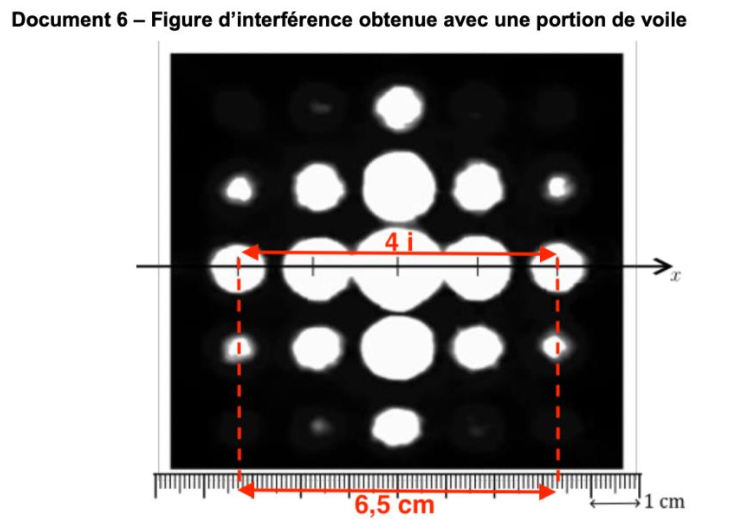
Le document 6 reproduit, à taille réelle, la figure d’interférence obtenue avec une portion de la voile. Cette figure n’est plus constituée de franges mais de points régulièrement espacés suivant deux directions principales.

Document 6 – Figure d’interférence obtenue avec une portion de voile

Source de lumière utilisée : diode laser de longueur d’onde 𝜆 = 650 nm.

Dans le cas d’un tissage régulier comme celui de la voile, on peut montrer que la relation entre l’interfrange 𝑖 et l’espacement des fils 𝑏 conserve la même expression, l’interfrange étant désormais défini comme l’intervalle entre les centres de deux points voisins.

Données :

• 𝐷 = 0,60 m ; 𝑢(𝐷) = 0,01 m.
• 𝜆 = 650 nm ; 𝑢(𝜆) = 10 nm.
• Relation entre les incertitudes-types :

$$\frac{u(b)}{b}=\sqrt{\left(\frac{u(D)}{D}\right)^2+\left(\frac{u(i)}{i}\right)^2+\left(\frac{u(\lambda)}{\lambda}\right)^2}$$

Q11- Déterminer la valeur de l’interfrange 𝑖 de la figure d’interférence du document 6, page 6 avec le plus de précision possible. Expliquer la méthode employée (il est possible d’utiliser une règle graduée personnelle ou la règle insérée dans la figure).

Q12- Estimer l’incertitude-type sur cette mesure de l’interfrange. Détailler le raisonnement.

Lorsqu’on mesure les 4 interfranges, on le fait avec une règle graduée en mm.
On estime donc l’incertitude de lecture à 1 mm (certains estiment l’incertitude de lecture à la moitié d’une graduation soit 0,5 mm)
Ainsi :
$u\left(4i\right)=1\ \text{mm}$
$u\left(i\right)=\frac{1}{4}$
$u\left(i\right)=0,25=0,3\ \text{mm}$ (On ne garde qu’un chiffre significatif pour l’incertitude).

Q13- En déduire une estimation de la valeur de l’espacement 𝑏 avec son incertitude.

$i=\frac{D}{b}\lambda$
$i\times b=D\times\lambda$
$b=\frac{D\times\lambda}{i}$
$b=\frac{0,60\times650\times{10}^{-9}}{1,6\times{10}^{-2}}$
$b=2,44\times{10}^{-5}\ \text{m}$ (on garde 3 chiffres significatifs par rapport à l’incertitude qui arrive après)

Calculons l’incertitude :
$\frac{u\left(b\right)}{b}=\sqrt{\left(\frac{u\left(D\right)}{D}\right)^2+\left(\frac{u\left(i\right)}{i}\right)^2+\left(\frac{u\left(\lambda\right)}{\lambda}\right)^2}$
$u\left(b\right)=b\times\sqrt{\left(\frac{u\left(D\right)}{D}\right)^2+\left(\frac{u\left(i\right)}{i}\right)^2+\left(\frac{u\left(\lambda\right)}{\lambda}\right)^2}$
$u\left(b\right)=2,44\times{10}^{-5}\times\sqrt{\left(\frac{0,01}{0,60}\right)^2+\left(\frac{0,3\times{10}^{-3}}{1,6\times{10}^{-2}}\right)^2+\left(\frac{10}{650}\right)^2}$
$u\left(b\right)=7,2\times{10}^{-7}\ \text{m}=8\times{10}^{-7}\ \text{m}$ (On ne garde qu’un chiffre significatif pour l’incertitude).

Ainsi :
$b=2,44\times{10}^{-5}\ \pm8\times{10}^{-7}\ \text{m}$
$b=\left(24,4\ \pm0,8\right)\times{10}^{-6}\ \text{m}$
$b=24,4\ \pm0,8\ \mu\text{m}$

Pour la voile étudiée, l’espacement 𝑏 varie d’une zone à l’autre de la voile en fonction des contraintes qui s’exercent sur la zone :

• Dans les zones soumises à de faibles contraintes, 𝑏 = 25 μm.
• Lorsque les contraintes sont importantes, le tissage est plus serré (𝑏 diminue) jusqu’à la valeur limite 𝑏 = 12 μm pour les contraintes les plus fortes.

Q14- Discuter la compatibilité de la mesure obtenue à la question Q13 avec le tissage d’une zone soumise à de faibles contraintes.

Méthode 1 :
$b=24\ \pm0,8\ \mu\text{m}$
$23,6\ \mu\text{m}<b<=25,2\ \mu\text{m}$
La valeur donnée par l’énoncé dans les zones soumises à de faibles contraintes, 𝑏 = 25 μm est bien comprise dans l’intervalle.
Ainsi, la mesure obtenue à la question Q13 avec le tissage d’une zone soumise à de faibles contraintes sont compatibles.

Méthode 2 :
Calculons le z-score :
$z=\frac{b_{\text{exp}}-b_{\text{théorique}}}{u_b}$
$z=\frac{\left|24,4-25\right|}{0,8}$
$z=0,75$
Le z-score est inférieur à 2 : la mesure obtenue à la question Q13 avec le tissage d’une zone soumise à de faibles contraintes sont compatibles.

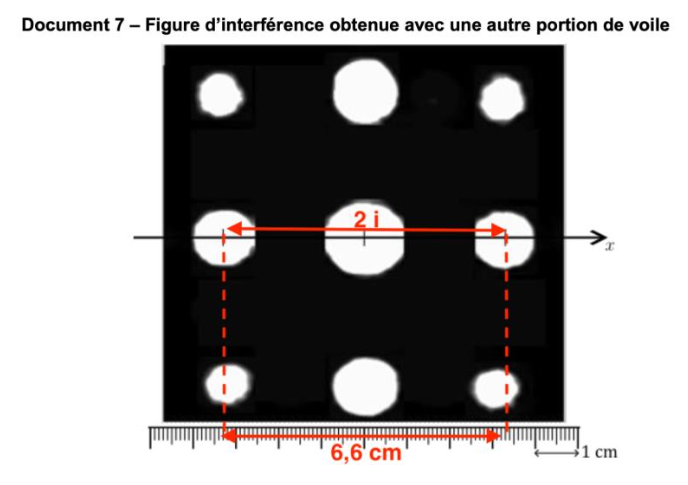
On réalise une seconde figure d’interférence avec une autre portion de la voile. La figure obtenue est représentée dans le document 7.

Q15- Justifier que cette portion de voile est prévue pour supporter des contraintes plus fortes que celle étudiée précédemment.

Dans cette question, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

Document 7 – Figure d’interférence obtenue avec une autre portion de voile

Déterminons $b$ :
$i=\frac{D}{b}\lambda$
$i\times b=D\times\lambda$
$b=\frac{D\times\lambda}{i}$
$b=\frac{0,60\times650\times{10}^{-9}}{3,3\times{10}^{-2}}$
$b=1,2\times{10}^{-5}\ \text{m}$
$b=12\times{10}^{-6}\ \text{m}$
$b=12\ \mu\text{m}$

D’après l’énoncé : Lorsque les contraintes sont importantes, le tissage est plus serré (𝑏 diminue) jusqu’à la valeur limite 𝑏 = 12 μm pour les contraintes les plus fortes.
Ainsi, cette portion de voile est prévue pour supporter des contraintes plus fortes que celle étudiée précédemment.