Enseignement scientifique première partie mathématique
Durée 0h48 – 12 points
Télécharger l’exercice en PDF :
Les trois parties sont indépendantes.
Partie A
Une étude portant sur les nuitées réservées par des touristes français et étrangers via une plateforme internet a donné les résultats suivants :
- 19 000 000 nuitées ont été réservées dans les trois plus grandes villes françaises : Paris, Marseille et Lyon.
- 79 % des touristes ont préféré Paris et parmi eux, 70 % sont des touristes étrangers.
- 1 910 000 nuitées ont été réservées à Lyon dont 788 000 par des touristes étrangers.
- À Marseille, 800 000 touristes étrangers ont réservé des nuitées.
1- Recopier et compléter le tableau suivant :
| Nombre de nuitées (en milliers) | Touristes français | Touristes étrangers | Total |
| Paris | |||
| Lyon | 788 | ||
| Marseille | |||
| Total | 19000 |
2- Dans l’ensemble de cette question 2, les pourcentages seront arrondis au dixième.
2-a- Quel est le pourcentage de touristes étrangers qui ont réservé via cette plateforme ?
2-b- Quel est le pourcentage de touristes qui ont réservé à Marseille et qui sont français ?
2-c- À Lyon, quel est le pourcentage de touristes étrangers qui ont réservé via cette plateforme ?
Partie B
Sur cette plateforme internet, 35 % des clients choisissent de réserver dans un camping, et parmi eux 66 % sont français. 27 % de ceux qui n’ont pas réservé dans un camping sont des clients étrangers.
On choisit au hasard un client ayant réservé via cette plateforme internet. On considère les événements suivants :
- C : « le client a réservé dans un camping » ;
- F : « le client est français ».
3- Recopier et compléter l’arbre pondéré représentant la situation :
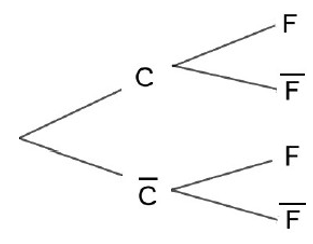
4- Calculer la probabilité que le client choisi soit français et qu’il ait réservé dans un camping.
5- On admet que p(F) = 0,7055. Le client choisi est français. Quelle est la probabilité qu’il ait réservé dans un camping ? On arrondira le résultat au millième.
Partie C
Une autre étude a permis de constater que le bénéfice par client réalisé par cette plateforme internet dépend du temps de connexion 𝑥, exprimé en minute. Pour les 20 premières minutes de connexion d’un client, ce bénéfice, exprimé en centimes, peut être modélisé par une fonction 𝑓 définie sur [ 0 ; 20] par :
𝑓(𝑥) = −2𝑥3 + 54𝑥2 − 270𝑥 − 80.
6- Calculer 𝑓(0) et interpréter ce résultat.
7- On admet que 𝑓 est dérivable sur [ 0 ; 20]. Calculer 𝑓’ (𝑥) pour 𝑥 ∈ [ 0 ; 20].
8- Montrer que 𝑓′(𝑥) = −6(𝑥 − 3)(𝑥 − 15) pour 𝑥 ∈ [ 0 ; 20].
9- Dresser le tableau des variations de 𝑓 sur [ 0 ; 20].
10- Pour les 20 premières minutes, quel temps de connexion du client, en minutes, permet d’assurer un bénéfice maximal pour la plateforme ? Quelle est la valeur de ce bénéfice ?
