E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02704, n°G1SPHCH02743 et n°G1SPHCH02767
Télécharger l’exercice en PDF :
La loi 2 de l’International Football Association Board a fixé les caractéristiques d’un ballon utilisé pour les compétitions internationales : le ballon doit être sphérique, en cuir ou dans une autre matière adéquate, avoir un diamètre de 22 cm et la pression de l’air dans le ballon doit être comprise entre 1,6×105 Pa et 2,1×105 Pa.
D’après http://www.theifab.com/fr/laws/chapter/22/section/31/
L’objectif de cet exercice est d’étudier le gonflage d’un ballon et son utilisation dans des lieux de compétitions d’altitude différente. Nous nous intéresserons ainsi à deux lois liées à cette situation : la loi de Mariotte, qui permet d’étudier le gonflage et la loi de statique des fluides qui permet de réfléchir à l’influence de l’altitude sur le gonflage.
- Étude expérimentale et utilisation de la loi de Mariotte.
Une expérience est menée au laboratoire pour tester la loi de Mariotte à l’aide d’un microcontrôleur et d’un capteur de pression.
On suit le protocole expérimental suivant :
① remplir initialement une seringue avec 30 cm3 d’air ;
② relier la seringue au capteur de pression connecté à un microcontrôleur ;
③ téléverser le programme « Mesure Pression » présenté ci-dessous dans le microcontrôleur ;
④ faire varier le volume du gaz dans la seringue et noter alors la valeur de la pression correspondante affichée sur l’écran LCD relié au microcontrôleur.

1.1. Adaptation du programme « Mesure Pression »
Un extrait du programme associé au pilotage du microcontrôleur dans le montage expérimental précédent est donné ci-dessous.

1.1.1. Indiquer en quelle unité la pression mesurée par le capteur sera affichée sur l’écran.
La pression mesurée par le capteur sera affichée en hPa
1.1.2. Dans le programme, la valeur de la pression est affichée sans décimale. Expliquer comment modifier la ligne 39 du programme pour que la valeur de la pression soit affichée avec 2 décimales.
lcd.print(Pression,2)
1.1.3. Expliquer comment modifier la ligne 43 pour que les mesures soient faites toutes les 3 secondes.
delay(3000)
1.2. Traitement de mesures obtenues en faisant varier le volume du gaz
Pour chaque volume d’air choisi dans la seringue, le microcontrôleur indique des valeurs de pression toutes les 2 secondes. Ces valeurs sont très proches, mais fluctuent légèrement.
Le tableau ci-dessous rassemble les valeurs de la pression P affichée par l’écran LCD du microcontrôleur pour différents volumes du gaz dans la seringue :
| V (cm3) | 20 | 25 | 30 | 35 | 40 | 50 |
| P (hPa) | 1505 | 1195 | 998 | 852 | 745 | 600 |
1.2.1. Énoncer la loi de Mariotte.
Pour une quantité de gaz constante, à une température constante le produit de la pression p et du volume V est constant : P.V=Constante
1.2.2. Exploiter ces mesures pour tester la loi de Mariotte. On explicitera précisément la méthode utilisée.
Calculons P.V pour chaque mesure :
| V (cm3) | 20 | 25 | 30 | 35 | 40 | 50 |
| P (hPa) | 1505 | 1195 | 998 | 852 | 745 | 600 |
| P.V(hPacm3) | 3,0.104 | 3,0.104 | 3,0.104 | 3,0.104 | 3,0.104 | 3,0.104 |
Nous remarquons que P.V=Constante
1.3. Gonflage d’un ballon de football
On utilise un gonfleur électronique de ballon ayant les caractéristiques suivantes :
- débit d’air à l’entrée du gonfleur : 4 litres par minute ;
- arrêt automatique quand la pression souhaitée est atteinte.

On souhaite gonfler, à l’aide de ce gonfleur, un ballon de football de compétition de diamètre égal à 22 cm pour obtenir une pression de l’air à l’intérieur du ballon de 2,1×105 Pa.
On admet qu’avant le gonflage le ballon est totalement dégonflé et que le volume d’air à l’intérieur est négligeable. On admet également que la température reste constante pendant le gonflage. On précise que l’air entrant dans le compresseur est à la pression atmosphérique.
1.3.1. On appelle V0 le volume d’air à prélever dans le milieu extérieur pour le gonflage, V1 et P1 le volume d’air et la pression à l’intérieur du ballon une fois qu’il est gonflé.
Montrer que $ V_0=\frac{P_1 \times V_1}{P_0}$ .
Loi de Mariotte : P.V=Constante
P0.V0=P1.V1
$ V_0=\frac{P_1 \times V_1}{P_0}$
1.3.2. Montrer que la durée nécessaire au gonflage, à l’aide du gonfleur électronique, est voisine de 3 minutes.
V1 est le volume du ballon :
$V_1=\frac{4}{3}\pi r^3$
$V_0=\frac{P_1\times\frac{4}{3}\pi r^3}{P_0}$
$V_0=\frac{2,1.10^5\times\frac{4}{3}\pi(11)^3}{1,013.10^5}=1,2.10^4\ cm^3=12L$
Or le débit d’air à l’entrée du gonfleur : 4 litres par minute ; il faudra donc 3 minutes pour gonfler le ballon.
- Données :
| Pression atmosphérique | Volume d’une sphère de rayon R | Unités de volume |
| P0 = 1,013 × 105 Pa | $ V=\frac{4}{3} \times \pi \times R^3$ | 1 litre correspond à 103 cm3 |
2. Utilisation du ballon dans des lieux de compétitions d’altitudes différentes.
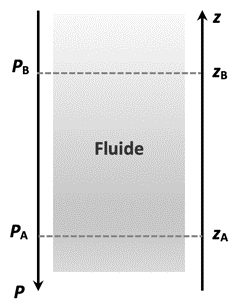
On s’intéresse dans cette partie à la loi fondamentale de la statique des fluides pour modéliser l’évolution de la pression atmosphérique en fonction de l’altitude. Cette loi précise que, pour un fluide au repos incompressible de masse volumique ρ , la différence de pression entre deux points, A et B, s’exprime par la relation : PA – PB = ρ×g×(zB – zA).
Dans cette relation :
- la masse volumique ρ s’exprime en kg×m-3 ;
- l’intensité de pesanteur g s’exprime en N×kg–1 ;
- les altitudes zA et zB s’expriment en m et sont repérées sur un axe vertical ascendant Oz.
Les villes de Denver et de New York se sont portées candidates pour accueillir les matchs de la coupe du monde de football 2026 organisée conjointement par les États-Unis, le Canada et le Mexique.
2.1. Comparer qualitativement la valeur de la pression au point A à celle au point B.
$P_B-P_A=\rho\times g\times(z_A-z_B)$
Or $z_A<z_B$
$\Rightarrow(z_A-z_B)<0$
$\Rightarrow\rho\times g\times(z_A-z_B)<0$
$\Rightarrow P_B-P_A<0$
$\Rightarrow P_B<P_A$
2.2. Évaluer la différence de pression atmosphérique PNY – PD entre les villes de New York située à 10 mètres d’altitude et de Denver située à 1600 mètres d’altitude. Pour les deux villes, on suppose que la masse volumique de l’air a pour valeur ρ = 1,1 kg×m-3 et et que l’intensité de la pesanteur a pour valeur g = 9,8 N×kg-1.
$P_{NY}-P_D=\rho\times g\times(z_D-z_{NY})$
$P_{NY}-P_D=1,1\times9,8\times(1600-10)=1,7.10^4\ Pa$
2.3. Sur le site Planet-Terre de l’École Normale Supérieure de Lyon, différents modèles de l’atmosphère sont proposés.
- Modèle 1 : la masse volumique de l’air dépend de la pression et de la température. On suppose que la température varie selon une fonction affine décroissante de l’altitude.
- Modèle 2 : la masse volumique de l’air est constante, quelle que soit l’altitude.
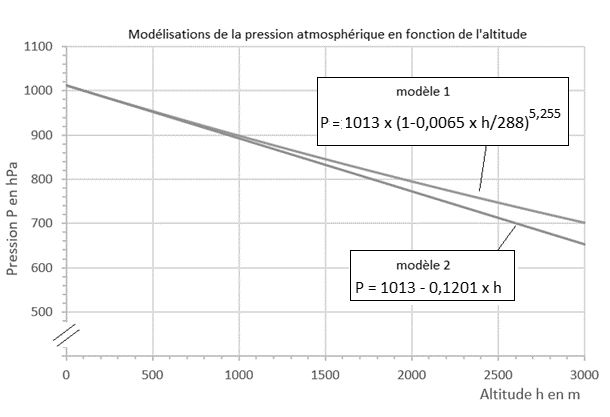
Les graphes correspondants à chacun des deux modèles, et représentant l’évolution de la pression atmosphérique en fonction de l’altitude, sont donnés ci-dessous (par souci d’échelle l’axe vertical n’est pas gradué à partir de l’origine).
On considère que ces deux modèles sont équivalents quand les valeurs de pression qu’ils donnent diffèrent entre elles de moins de 5 %.
2.3.1. Auquel des modèles 1 ou 2 est liée la loi fondamentale de la statique des fluides ?
$P_B-P_A=\rho\times g\times(z_A-z_B)$
Soit l’altitude h , $P_A$ la pression à l’altitude $z_A=0\ m$ soit la pression atmosphérique :
$P_A=P_0=1,013.10^5\ Pa=1013hPa$
$h=z_B-z_A$
$\Rightarrow P_B-P_A=\rho\times g\times-h$
$\Rightarrow P_B=P_A+\rho\times g\times-h$
$\Rightarrow P_B=P_A-\rho\times g\times h$ Ce qui correspond au modèle 2
2.3.2. Au vu des graphiques ci-dessus, l’utilisation de cette loi pour répondre à la question 2.2 parait-elle justifiée ?
Calculons à l’aide des deux modèles la pression demandée à la question 2.2
Pour une altitude h=10m
Modèle 1 : $P=1013\times(1-0,0065\times h/288)^{5,255}$
$P=1013\times(1-0,0065\times10/288)^{5,255}=1012\ hPa$
Modèle 2 : $P=1013-0,1201\times h$
$P=1013-0,1201\times10=1012\ hPa$
Les deux modèles donnent le même résultat
Pour une altitude h=1600m
Modèle 1 : $P=1013\times(1-0,0065\times h/288)^{5,255}$
$P=1013\times(1-0,0065\times1600/288)^{5,255}=835\ hPa$
Modèle 2 : $P=1013-0,1201\times h$
$P=1013-0,1201\times1600=821\ hPa$
On considère que ces deux modèles sont équivalents quand les valeurs de pression qu’ils donnent diffèrent entre elles de moins de 5 %.
Calculons écart relatif entre les 2 valeurs :
$\left|\frac{835-821}{821}\right|=0,017=1,7%$
Ces deux modèles sont donc équivalents, on peut donc considérer que la masse volumique de l’air est constante, quelle que soit l’altitude.
L’utilisation de la loi de la statique des fluides est donc justifiée.
