Bac Liban 2023 Sujet 1
Exercice 1 – (11 points) – Durée 1h45 – Calculatrice autorisée
Sujet n°23-PYCJ1LI1
Sujet et corrigé
EXERCICE 1 : UN « JET DE 7 MÈTRES » AU HANDBALL (11 POINTS)

Source : hbcnantes.com
Lors du match de handball opposant le club du HBC Nantes à l’US Ivry en 2020 au palais des sports de Beaulieu, le joueur nantais Valero Rivera se trouve face au gardien adverse pour un « jet de 7 mètres », le joueur étant placé à 7 mètres du but – l’équivalent du pénalty au football. Parmi les diverses options de tir qui s’offrent à lui, il choisit le lob, une trajectoire en cloche au-dessus du gardien avancé.
Les objectifs de l’exercice sont, dans une première partie, d’étudier le mouvement d’un ballon lors d’un tir similaire filmé, et dans une seconde partie, d’étudier quelques caractéristiques des ondes sonores perçues à l’intérieur du palais des sports.
Les deux parties de cet exercice sont indépendantes.
A. Étude du mouvement d’un ballon lors du tir au-dessus du gardien
Un « jet de 7 mètres » a été reproduit et filmé au gymnase, la chronophotographie du mouvement du ballon est la suivante :

Données :
- intensité du champ de pesanteur terrestre : g= 9,81 m·s-2 ;
- constante universelle de gravitation : G= 6,67.10-11 m3·kg-1·s-2 ;
- hauteur de la barre transversale d’un but de handball : 2,0 m.
Dans cette étude :
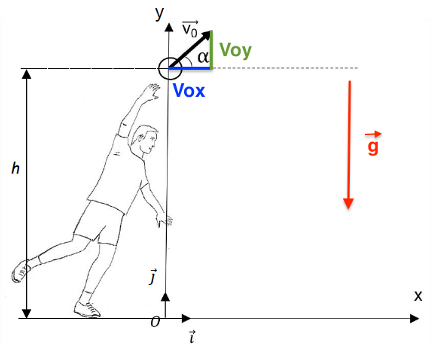
- Le système étudié est le ballon, les coordonnées de la position de son centre de masse G sont notées (x ; y) dans le repère $\mathcal{R}\left(O,\vec{i},\vec{j}\right)$
- Dans ce repère, les coordonnées du vecteur vitesse du ballon sont notées (vx ; vy) et celles de son vecteur accélération sont notées (ax ; ay).
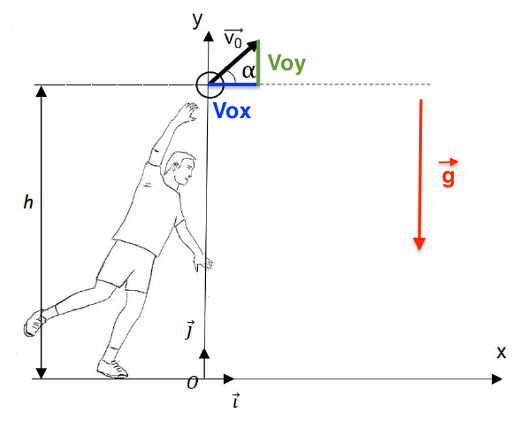
- Le vecteur vitesse initiale$\overrightarrow{V_0}$ du ballon forme un angle α avec l’horizontale.
- L’action de l’air sur le ballon est négligée.
- L’instant t = 0 correspondant à l’origine des dates est choisi juste après que le ballon a quitté la main du tireur. À cet instant, les coordonnées du centre de masse G du ballon sont (x0 = 0 ; y0 = h = 2,34 m)
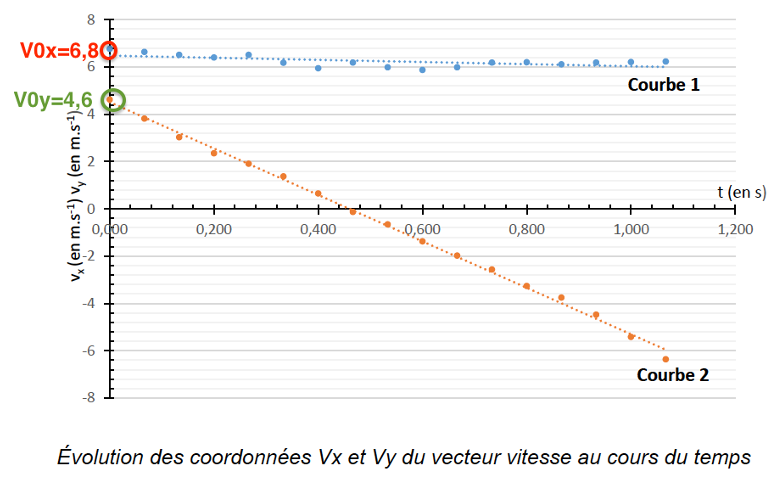
- Les courbes représentant les coordonnées du vecteur vitesse au cours du temps, après étalonnage du repère et pointage des positions successives du centre du ballon, sont données ci-dessous :
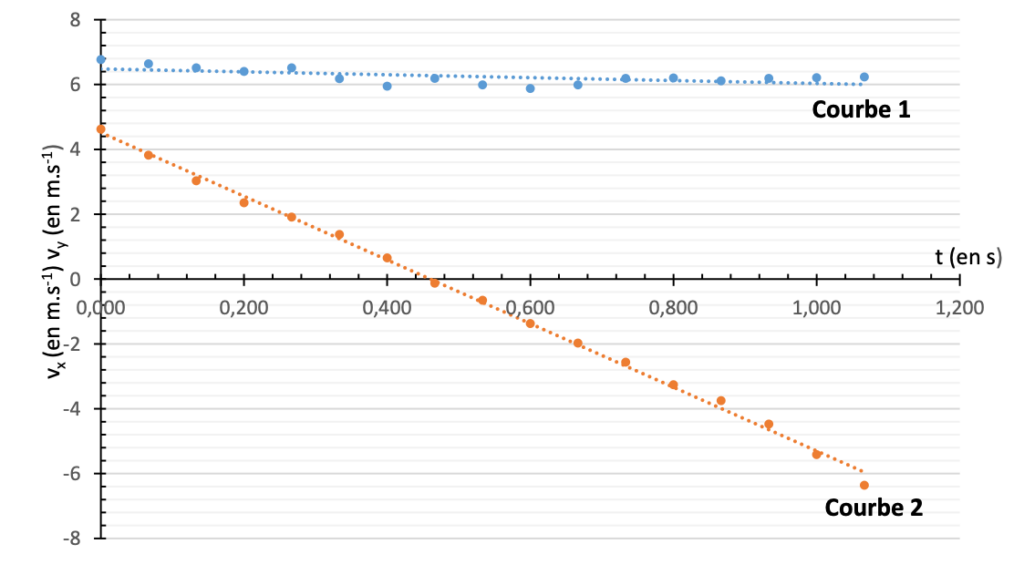
Évolution des coordonnées Vx et Vy du vecteur vitesse au cours du temps
Q.1. Nommer le référentiel dans lequel la trajectoire du ballon est observée sur la chronophotographie.
Le référentiel dans lequel la trajectoire du ballon est observée sur la chronophotographie est le référentiel terrestre.
Q.2. En précisant certaines hypothèses, établir l’expression du vecteur accélération du centre de masse du ballon lors du tir. Établir les coordonnées de ce vecteur dans le repère $\mathcal{R}\left(O,\vec{i},\vec{j}\right)$
Système : ballon
Référentiel terrestre supposé galiléen.
Hypothèse : L’action de l’air sur le ballon est négligée.
D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a_G}$$
$$\overrightarrow{P}=m\overrightarrow{a_G}$$
$$m\overrightarrow{g}=m\overrightarrow{a_G}$$
$$\overrightarrow{g}=\overrightarrow{a_G}$$
$$\overrightarrow{a_G}=\overrightarrow{g}$$
Or
$$\overrightarrow{g}\left|\begin{matrix}0\\-g\end{matrix}\right.$$
Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.
$$\overrightarrow{a_G}\left|\begin{matrix}a_{x(t)}=0\\a_{y(t)}=-g\end{matrix}\right.$$
Q.3. Parmi les expressions proposées pour l’intensité du champ de pesanteur terrestre, déterminer par analyse dimensionnelle celle qui est homogène (on note MT la masse de la Terre et RT son rayon) :
a) $g=\frac{G\cdot M_T^2}{R_T}$
b) $g=\frac{G\cdot M_T}{R_T^2}$
c) $g=\frac{G+M_T}{R_T^2}$
G s’exprime en $m^3\cdot {\rm kg}^{-1}\cdot s^{-2}$
$M_T$ s’exprime en kg
$R_T$ s’exprime en m
$g$ s’exprime en $m\cdot s^{-2}$
$$g=\frac{G\cdot {M_T}^2}{R_T}$$
$$\frac{\left[G\right]\cdot \left[M_T\right]^2}{\left[R_T\right]}$$
$$\frac{m^3\cdot {\rm kg}^{-1}\cdot s^{-2}\cdot {\rm kg}^2}{m}$$
$$m^2\cdot kg\cdot s^{-2}\neq\left[g\right]=m\cdot s^{-2}$$
Cette expression n’est pas homogène.
$$g=\frac{G\cdot M_T}{{R_T}^2}$$
$$\frac{\left[G\right]\cdot \left[M_T\right]}{\left[R_T\right]^2}$$
$$\frac{m^3\cdot {\rm kg}^{-1}\cdot s^{-2}\cdot kg}{m^2}$$
$$m\cdot s^{-2}=\left[g\right]=m\cdot s^{-2}$$
Cette expression est homogène.
$$g=\frac{G+{M_T}^2}{{R_T}^2}$$
$$\frac{\left[G\right]+\left[M_T\right]^2}{\left[R_T\right]^2}$$
$$\frac{m^3\cdot {\rm kg}^{-1}\cdot s^{-2}+{\rm kg}^2}{m^2}$$
$$m\cdot {\rm kg}^{-1}\cdot s^{-2}+m^{-2}{\rm kg}^2\neq\left[g\right]=m\cdot s^{-2}$$
Cette expression n’est pas homogène.
L’expression qui est homogène est
$$g=\frac{G\cdot M_T}{{R_T}^2}$$
Q.4. Montrer que les expressions des coordonnées du vecteur vitesse du centre de masse du ballon lors du tir sont :
vx(t) = v0· cos (α) ; vy(t) = -g·t + v0· sin (α)
$$\overrightarrow{a_G}=\frac{d\overrightarrow{v_G}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{v_G}\left|\begin{matrix}v_{x(t)}=C_1\\v_{y(t)}=-gt+C_2\end{matrix}\right.$$
Pour trouver les constantes, on utilise $\overrightarrow{v_0}$
$$\overrightarrow{v_0}\left|\begin{matrix}v_{ox}=v_0\cos\left(\alpha\right)\\v_{0y}=v_0\sin\left(\alpha\right)\end{matrix}\right.$$
d’ou
$$\overrightarrow{v_G}\left|\begin{matrix}v_{x(t)}=v_0\cos\left(\alpha\right)\\v_{y(t)}=-gt+v_0\sin\left(\alpha\right)\end{matrix}\right.$$
Q.5. Sur le graphique représentant l’évolution des coordonnées du vecteur vitesse au cours du temps, identifier la courbe correspondant à vx et celle correspondant à vy. Justifier.
$v_{x(t)}=v_0\cos\left(\alpha\right)$ : $v_x$ est indépendant du temps, $v_x$ est constant : courbe 1.
$v_{y(t)}=-gt+v_0\sin\left(\alpha\right)$ : $v_y$ est une fonction affine avec un coefficient directeur négatif , $v_y$ est décroissant : courbe 2.

Q.6. Calculer à partir de ces courbes la norme v0 du vecteur vitesse initiale, ainsi que la valeur de l’angle α.
$$v_0=\sqrt{\left(v_{ox}\right)^2+\left(v_{0y}\right)^2}$$
$$v_0=\sqrt{\left(6,8\right)^2+\left(4,6\right)^2}$$
$$v_0=8,2\ m.s^{-1}$$
$$v_{ox}=v_0\cos\left(\alpha\right)$$
$$\cos\left(\alpha\right)=\frac{v_{ox}}{v_0}$$
$$\cos\left(\alpha\right)=\frac{6,8}{8,2}$$
$$\cos\left(\alpha\right)=0,83$$
$$\alpha=\arccos\left(0,83\right)=34°$$
Q.7. Établir les équations horaires x(t) et y(t) du mouvement lors du tir.
$$\overrightarrow{v_G}=\frac{d\overrightarrow{OG}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{OG}(t)\left|\begin{matrix}x(t)=v_0\times\cos\left(\alpha\right)\times t+C_3\\y(t)=-\frac{1}{2}\times g\times t^2+v_0\times\sin\left(\alpha\right)\times t+C_4\end{matrix}\right.$$
Pour trouver les constantes, on utilise $\overrightarrow{OG}_(0)$
$$\overrightarrow{OG}_(0)\left|\begin{matrix}x_0=0\\y_0=h\end{matrix}\right.$$
d’ou
$$\overrightarrow{OG}(t)\left|\begin{matrix}x(t)=v_0\times\cos\left(\alpha\right)\times t\\y(t)=-\frac{1}{2}\times g\times t^2+v_0\times\sin\left(\alpha\right)\times t+h\end{matrix}\right.$$
Q.8. En déduire que l’équation y(x) de la trajectoire s’écrit :
$$y(x)=-\frac{1}{2}\cdot g\cdot\frac{x^2}{v_0^2\cdot\cos^2(\alpha)}+\tan(\alpha)\cdot x+h$$
On isole $t$ :
$$x=v_0\cos\left(\alpha\right)\times t$$
$$t=\frac{x}{v_0\cos\left(\alpha\right)}$$
On remplace $t$ dans $y$ :
$$y(x)=-\frac{1}{2}g\frac{x^2}{v_0^2\cos^2\left(\alpha\right)}+\tan\left(\alpha\right)\cdot x+h$$
Q.9. Le gardien étant situé à 4,0 m du tireur, déterminer si le « jet de 7 mètres » étudié permet de marquer un but. On considère que le gardien peut atteindre avec son bras levé une hauteur maximale de 2,8 m en plein saut.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
Déterminer si le « jet de 7 mètres » étudié permet de marquer un but.
1ère condition :
$$y(x_g)=3,3\ m$$
Le gardien ne peut pas toucher la balle.
2nd condition :
$$y(x_c)=1,9\ m$$
La balle entre dans les cages.
Le « jet de 7 mètres » étudié permet donc de marquer un but.
B. Étude des ondes sonores produites par le sifflet de l’arbitre
Lors d’un « jet de 7 mètres », l’arbitre est placé à proximité du but. Il donne un bref coup de sifflet pour indiquer au joueur qu’il peut déclencher son tir. Le niveau d’intensité sonore L perçu par l’arbitre, dont l’oreille est située à une distance de 15 cm du sifflet, est égal à 115 dB.
Données :
- le niveau d’intensité sonore, noté L, est lié à l’intensité sonore I par la relation :
$$L=10\log\left(\frac{I}{I_0}\right)$$
avec L exprimé en dB, I et I0 en W·m-2 et I0 = 1,0 x 10-12 W·m-2 (intensité sonore correspondant au seuil d’audibilité) ;
- une source S, émettant des ondes sonores de puissance P, est isotrope si elle émet la même quantité d’énergie dans toutes les directions. L’intensité sonore mesurée, notée I, dépend alors de la distance d selon la relation (ou d exprimée en m est la distance qui sépare le récepteur de la source) :
$$I=\frac{P}{4\pi\cdot d^2}$$
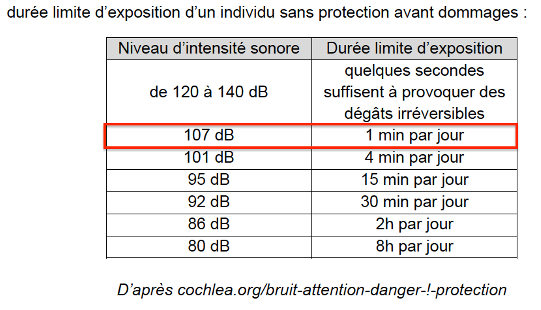
- durée limite d’exposition d’un individu sans protection avant dommages :
| Niveau d’intensité sonore | Durée limite d’exposition |
| de 120 à 140 dB | quelques secondes suffisent à provoquer des dégâts irréversibles |
| 107 dB | 1 min par jour |
| 101 dB | 4 min par jour |
| 95 dB | 15 min par jour |
| 92 dB | 30 min par jour |
| 86 dB | 2h par jour |
| 80 dB | 8h par jour |
D’après cochlea.org/bruit-attention-danger-!-protection
Q.10. Au cours d’un match, l’arbitre donne environ 200 coups de sifflet. La durée moyenne du coup de sifflet étant de 0,3 s, indiquer si l’arbitre encourt un risque auditif. Justifier.
Le niveau d’intensité sonore L perçu par l’arbitre, dont l’oreille est située à une distance de 15 cm du sifflet, est égal à 115 dB.
L’arbitre donne environ 200 coups de sifflet. La durée moyenne du coup de sifflet étant de 0,3 s,
$$\Delta t=200\times0,3=60\ s=1\ min$$
Pour 107 dB, la durée limite d’exposition est d’une minute par jour. L’arbitre est exposé à 115 dB pour une durée d’une minute au cours d’un match : l’arbitre encourt donc un risque auditif.
Q.11. Proposer une solution simple que l’arbitre pourrait envisager pour se protéger. Nommer le type d’atténuation correspondant.
Pour se protéger, l’arbitre pourrait utiliser des protections auditives. Il s’agit d’une atténuation par absorption.
Q.12. Calculer l’intensité sonore I perçue par l’arbitre sans protection lors du coup de sifflet.
$$L=10\log\left(\frac{I}{I_0}\right)$$
$$10\log\left(\frac{I}{I_0}\right)=L$$
$$\log\left(\frac{I}{I_0}\right)=\frac{L}{10}$$
$$\frac{I}{I_0}={10}^{\frac{L}{10}}$$
$$I=I_0\times{10}^{\frac{L}{10}}$$
$$I=1,0\times{10}^{-12}\times{10}^{\frac{115}{10}}$$
$$I=0,32\ W{.m}^{-2}$$
Q.13. Montrer que la puissance de la source sonore constituée par le sifflet est égale à P = 8,9×10-2 W.
$$I=\frac{P}{4\pi d^2}$$
$$\frac{P}{4\pi d^2}=I$$
$$P=I\times4\pi d^2$$
$$P=0,32\ \times4\pi\times\left(15\times{10}^{-2}\right)^2$$
$$P=9,0\times{10}^{-2}W$$
Un spectateur proche du terrain est situé à 5,0 m de l’arbitre. On admet que le seul son parvenant à son oreille est celui émis par le sifflet, considéré comme une source isotrope.
Q.14. Déterminer le niveau d’intensité sonore que ce spectateur perçoit.
$$L\prime=10\log\left(\frac{I\prime}{I_0}\right)$$
Or
$$I\prime=\frac{P}{4\pi{d\prime}^2}$$
$$L\prime=10\log\left(\frac{\frac{P}{4\pi{d\prime}^2}}{I_0}\right)$$
$$L\prime=10\log\left(\frac{P}{I_0\times4\pi{d\prime}^2}\right)$$
$$L\prime=10\log\left(\frac{9,0\times{10}^{-2}}{1,0\times{10}^{-12}\times4\pi\times{5,0}^2}\right)$$
$$L^\prime=85dB$$
Ce spectateur perçoit 85 dB.
Q.15. Déterminer la valeur de l’atténuation correspondant à la différence de niveau d’intensité sonore perçue entre l’arbitre et le spectateur à 5,0 m. Quel nom donne-t-on à ce type d’atténuation ?
$$A=L-L^\prime$$
$$A=115-85$$
$$A=30\ dB$$
C’est une atténuation géométrique.
En réalité, le son produit par le sifflet se superpose au bruit ambiant. En dehors des « pics » de bruit produits par le public manifestant sa joie suite à un but marqué ou par les coups de sifflets de l’arbitre, le niveau d’intensité sonore dû au bruit ambiant, perçu par chaque spectateur, est égal à 75 dB. À 15 m de l’arbitre, l’intensité sonore due au son du sifflet a même valeur que celle due au bruit ambiant.
Q.16. Déterminer le niveau d’intensité sonore global perçu par un spectateur à cette distance.
$$L=10\log\left(\frac{I}{I_0}\right)$$
$$L_T=10\log\left(\frac{I_T}{I_0}\right)$$
D’après l’énoncé : « À 15 m de l’arbitre, l’intensité sonore due au son du sifflet a même valeur que celle due au bruit ambiant. »
Ainsi $$I_T=I_{bruit\ ambiant}+I_{sifflet}=2I_{sifflet}$$
$$L_T=10\log\left(\frac{2I_{sifflet}}{I_0}\right)$$
$$L_T=10\log\left(2\right)+10\log\left(\frac{I_{sifflet}}{I_0}\right)$$
$$L_T=10\log\left(2\right)+L_{sifflet}$$
$$L_T=3+75$$
$$L_T=78\ dB$$
