Un poison radioactif

Enseignement scientifique première

Durée 1h – 10 points – Thème « Une longue histoire de la matière »

Un écrivain vous contacte pour achever un roman d’espionnage… Suspense !

Document 1 : lettre de l’écrivain à votre attention

Bonjour, je suis Jules Servadac, écrivain de roman policier. Je vous sollicite afin de valider quelques aspects scientifiques de mon roman.

Voici mes premières lignes :

« Pierre et Marie Curie ont découvert le polonium, juste avant le radium qui les rendit célèbres. Le polonium-210 (²¹⁰Po) est mille fois plus toxique que le plutonium, et un million de fois plus encore que le cyanure. Sachez que dix microgrammes (µg) sont nécessaires pour empoisonner un homme de poids moyen en quelques semaines et que cette dose mortelle est invisible à l’œil nu ».

Dans mon roman, Tiago, agent secret de Folivie, souhaite s’en servir pour éliminer un agent infiltré. Celui-ci dîne tous les soirs dans le même restaurant : l’agent secret compte en profiter pour « poivrer » à sa façon son dîner.

Pour cela, Tiago doit se procurer du polonium-210. Pour des raisons logistiques, il ne peut récupérer le polonium que 100 jours avant le dîner programmé dans un autre pays. Or le polonium perd la moitié de sa radioactivité tous les 138 jours.

J’ai deux problèmes à vous soumettre concernant la quantité de polonium que Tiago doit transporter :

Restera-t-il suffisamment de Polonium-210 radioactif à la fin de son voyage ?
La dose sera-t-elle invisible à l’œil nu ?

Document 2 : données relatives au polonium

Le polonium est l’un des rares éléments à cristalliser dans le réseau cubique simple.

Paramètre de maille : a = 3,359 x 10^-10 m.

Masse molaire du polonium : M(Po) = 209,98 g∙mol^-1.

Donnée complémentaire : nombre d’Avogadro NA = 6,022 x 10²³ mol^-1.

Il est rappelé que la masse molaire d’un élément est la masse d’une mole de quantité de matière de cet élément.

Partie 1 : la radioactivité du polonium

L’objectif est ici de vérifier qu’en partant avec 20 µg de polonium-210, il restera suffisamment de polonium radioactif à l’issue du voyage.

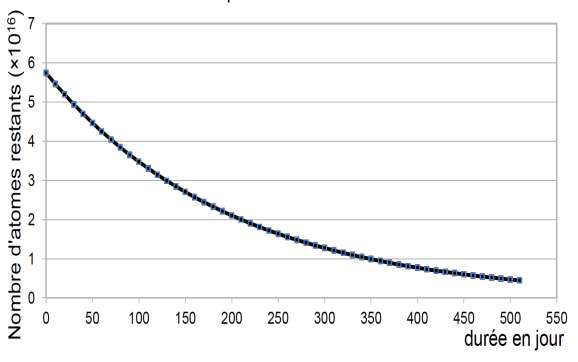
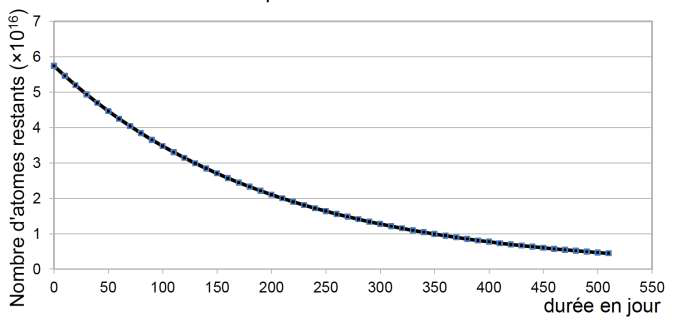
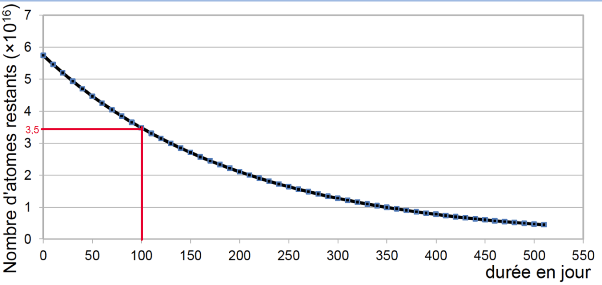
Document 3 : courbe de décroissance radioactive du polonium

Courbe de décroissance d’un échantillon de polonium 210

1 – Déterminer en µg la masse initiale de Polonium présente dans l’échantillon utilisé pour réaliser le graphique du document 3.

$m =n\times M$

$n =\frac{N}{N_A}$

D’ou

$m =\frac{N}{N_A}\times M$

Graphiquement N=5,8.10¹⁶

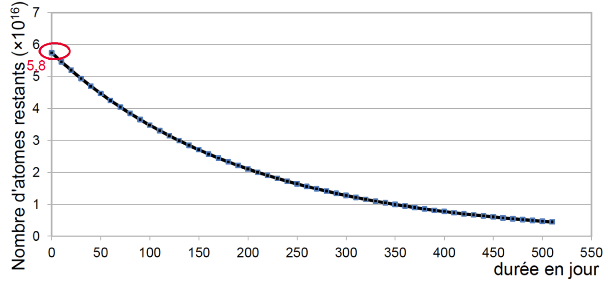
$m =\frac{5,8.10^{16}}{6,022.10^{23}}\times 209,98$

m=2,0.10^-5 g

m=20 μg

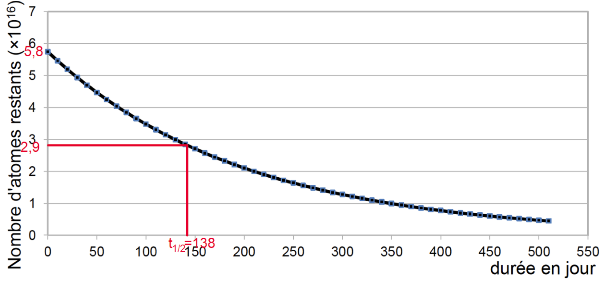
2 – Jules Servadac écrit dans son roman : « Le polonium perd la moitié de sa radioactivité tous les 138 jours ».

« Le polonium perd la moitié de sa radioactivité tous les 138 jours ». La grandeur physique sur laquelle il appuie cette affirmation est la demi-vie.

2-a- Définir scientifiquement la grandeur physique sur laquelle il appuie cette affirmation, en donnant son nom.

La demi-vie d’un élément radioactif est la durée nécessaire pour que la moitié des noyaux initialement présents se soient désintégrés.

2-b- La faire figurer sur le graphique du document réponse à rendre avec la copie en laissant apparents les traits de construction.

3 – Justifier par la méthode de votre choix que, pour l’échantillon considéré, la quantité de polonium restant après le voyage sera suffisante pour accomplir la mission.

Méthode n°1 :

« Pour des raisons logistiques, il ne peut récupérer le polonium que 100 jours avant le dîner programmé dans un autre pays. »

Graphiquement, au bout de 100 jours : N=3,5.10¹⁶

Calculons la masse de polonium correspondante à l’aide de la relation utilisée à la question 1 :

$m =\frac{N}{N_A}\times M$

$m =\frac{3,5.10^{16}}{6,022.10^{23}}\times 209,98$

m=1,2.10^-5 g

m=12 μg

« dix microgrammes (µg) sont nécessaires pour empoisonner un homme de poids moyen en quelques semaines »

La quantité restante est supérieure à 10 microgrammes : la quantité de polonium restant après le voyage sera suffisante pour accomplir la mission.

Méthode n°2 :

Initialementl’échantillon utilisé contient 20 microgrammes.

« dix microgrammes (µg) sont nécessaires pour empoisonner un homme de poids moyen en quelques semaines »

« Le polonium perd la moitié de sa radioactivité tous les 138 jours » : au bout de 138 jours il restera les dix microgrammes.

Au bout de 100 jours il restera donc plus que les 10 microgrammes : la quantité de polonium restant après le voyage sera suffisante pour accomplir la mission.

Partie 2 : la structure du polonium

L’objectif est ici de vérifier que les 10 µg de polonium dont Tiago a besoin pour empoisonner l’agent infiltré sont bien invisibles à l’œil nu.

4 – À partir de vos connaissances et des informations apportées par le document 3, répondre aux questions suivantes :

4-a- Représenter la structure cubique simple du polonium en perspective cavalière.

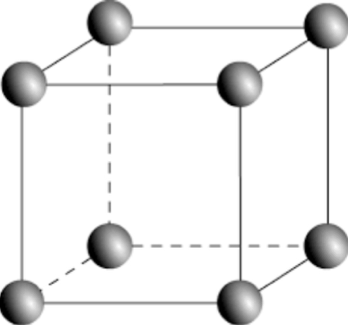
4-b- Dénombrer, en indiquant les calculs effectués, les atomes par maille.

Il y a 8 atomes sur les sommets qui sont dans 1/8 de la maille.

N=8×1/8=1

Il y a 1 atome dans une maille.

5- Montrer que la masse volumique du polonium est de 9,20 x 10⁶ g.m^-3.

$\rho =\frac{m_{maille}}{V_{maille}}$

$m_{maille} =N \times m$

$V_{maille}=a^3$

Calculons la masse d’un atome de polonium à l’aide de la relation utilisée à la question 1 :

$m =\frac{N}{N_A}\times M$

$m =\frac{1}{6,022.10^{23}}\times 209,98$

m=3,49.10^-22 g

$\rho =\frac{N \times m}{a^3}$

$\rho =\frac{1 \times 3,49.10^{-22}}{(3,359.10^{-10})^3}$

ρ=9,20 x 10⁶ g.m^-3

6- Comparaison avec la taille d’un grain de poivre.

6-a- Calculer le volume occupé par la masse de polonium utilisée par Tiago (10 µg).

$\rho =\frac{m}{V}$

$V=\frac{m}{\rho}$

$V=\frac{10.10^{-10}}{9,20.10^{6}}$

$V=1,1.10^{-12}m^3$

6-b- Sachant qu’un grain de poivre broyé occupe un volume d’environ 10^-10 m³ et est difficilement visible à l’œil nu, justifier que l’échantillon est invisible.

1,1.10^-12 m³<10^-10 m³ : le volume occupé par la masse de polonium utilisée par Tiago est inferieur au volume d’un grain de poivre broyé qui est difficilement visible à l’œil nu. Ainsi l’échantillon est invisible.

Document réponse à rendre avec la copie

Courbe de décroissance d’un échantillon de polonium 210