Bac Métropole Mars 2021 Sujet 2
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet et corrigé
Mot-clé : mouvement dans un champ de pesanteur uniforme

D’après redbull.com
Le 14 octobre 2012, Félix Baumgartner devient le premier homme à atteindre une vitesse égale à celle du son en s’élançant d’une capsule située dans la zone supérieure de la stratosphère.
L’objectif de cet exercice est de comprendre pourquoi il réalise un saut depuis la zone supérieure de la stratosphère pour atteindre la vitesse du son dans l’atmosphère.
Données :
- masse de Félix Baumgartner et de son équipement : m = 120 kg ;
- altitudes limites de la stratosphère : zmin = 11 km, zmax = 50 km ;
- altitude de la capsule au moment du saut : zdépart = 38 969 m ;
- intensité du champ de pesanteur à la surface de la Terre supposée sphérique de rayon RT : g0 = 9,81 m·s-2 ;
- rayon de la Terre : RT = 6 370 km ;
- expression du champ de pesanteur terrestre en fonction de l’altitude : $g(z) = \frac{g_0 \times R_T^2}{(R_T+z)^2} $
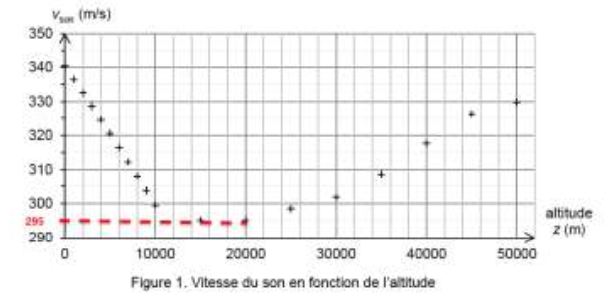
- évolution de la norme de la vitesse du son vson dans l’atmosphère en fonction de l’altitude :
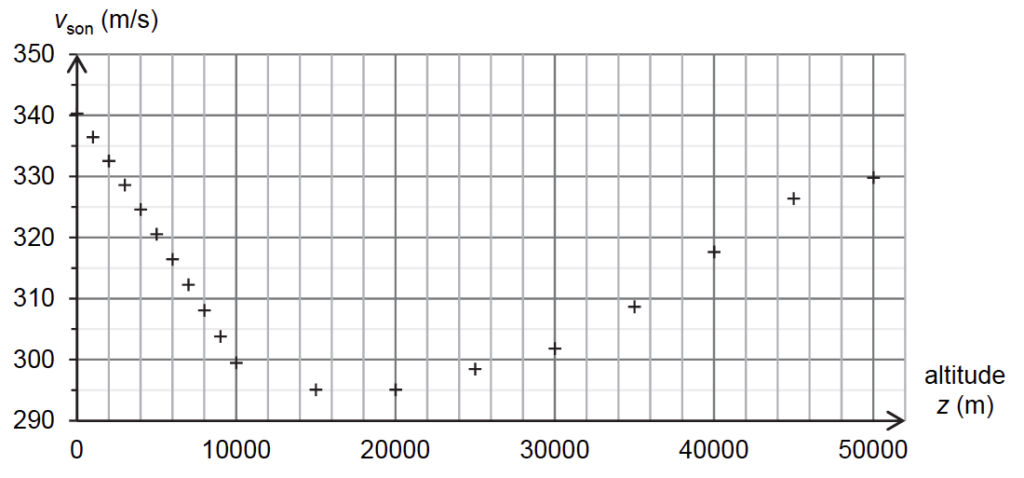
- norme f en N de la force de frottements due à l’air : f = 0,4 × ρair(z) × v2 avec :
- ρair(z) : masse volumique ρair de l’air à l’altitude z en kg·m-3 ;
- v : vitesse du centre de masse de Félix Baumgartner en m·s–1.
1. Influence de l’altitude sur le champ de pesanteur
1.1. Calculer la différence ∆g entre les valeurs des champs de pesanteur aux limites de la stratosphère définie par : ∆g = | g(zmax) – g(zmin) |.
$$\Delta g=\left|g\left(z_{max}\right)-g\left(z_{min}\right)\right|$$
Or
$$g\left(z\right)=\frac{g_0 \times R_T^2}{\left(R_T+z\right)^2}$$
$$\Delta g=\left|\frac{g_0 \times R_T^2}{\left(R_T+z_{max}\right)^2}-\frac{g_0 \times R_T^2}{\left(R_T+z_{min}\right)^2}\right|$$
$$ \Delta g=\left|\frac{9,81 \times {(6370{.10}^3)}^2}{\left(6370{.10}^3+50{.10}^3\right)^2}-\frac{9,81 \times {(6370{.10}^3)}^2}{\left(6370{.10}^3+11{.10}^3\right)^2}\right|$$
$$\Delta g=0,12$$
1.2. On considère que le champ de pesanteur est uniforme dans une zone de l’espace si sa variation par rapport à sa valeur à l’altitude zmax est inférieure à 2 %. Le champ de pesanteur terrestre peut-il être considéré comme uniforme dans la stratosphère ?
$$g\left(z_{max}\right)=\frac{9,81 \times {(6370{.10}^3)}^2}{\left(6370{.10}^3+50{.10}^3\right)^2}=9,66\ m{.s}^{-2}$$
$$\frac{ \Delta g}{g\left(z_{max}\right)}=\frac{0,12}{9,66\ }=0,012=1,2%$$
Pour la suite de l’exercice, on prend pour valeur du champ de pesanteur g = 9,66 m·s–2.
Le mouvement du centre de masse de Félix Baumgartner est étudié dans le référentiel terrestre supposé galiléen, l’axe des z est dirigé selon la verticale orientée vers le haut, l’origine O est prise au niveau du sol. À la date t = 0 s, Félix Baumgartner s’élance sans vitesse initiale. Son mouvement est supposé vertical.
2. Établir, dans le cadre du modèle de la chute libre, l’équation horaire z(t) de l’altitude du centre de masse de Félix Baumgartner à la date t en fonction de t, g et zdépart.
Réponse :
Système {Félix Baumgartner}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$\sum_{}^{}\overrightarrow{F}_{ext}=m\overrightarrow{a}$
$\overrightarrow{P}=m\overrightarrow{a}$
$m\overrightarrow{g}=m\overrightarrow{a}$
$\overrightarrow{a}=\overrightarrow{g}$
Or
$\overrightarrow{g} \begin{cases} 0 \\-g \end{cases}$
Projetons sur l’axe Oz :
$a_{z}(t)=-g $
$\overrightarrow{a}=\frac{d \overrightarrow{v}}{dt}$
On intègre l’acceleration:
$v_{z}(t)=-gt+C_{1}$
Pour trouver les constantes, on utilise $\overrightarrow{v_0}$ :
$ v_{0}=0$
d’ou
$v_{z}(t)=-gt $
$\overrightarrow{v}=\frac{d \overrightarrow{OM}}{dt}$
On intègre la vitesse :
$z(t)=-\frac{1}{2}gt^2+ C_{2}$
Pour trouver les constantes, on utilise $z_0$
$z_0=z_{départ} $
d’ou
$z(t)=-\frac{1}{2}gt^2+z_{départ}$
3. En déduire, dans le cadre de ce modèle, l’altitude à laquelle la valeur de la vitesse de Félix Baumgartner est égale à 307 m·s–1.
Pour trouver l’altitude à laquelle la valeur de la vitesse de Félix Baumgartner est égale à 307 ms–1, il faut trouver le temps pour lequel cette vitesse est atteinte et l’insérer dans l’altitude z.
$${\ v}_{z\left(t\right)}=-gt$$
$$t=\frac{{\ v}_{z\left(t\right)}}{-g}$$
$$z\left(t\right)=-\frac{1}{2}gt^2+z_{départ}$$
$$z\left(t\right)=-\frac{1}{2}g\left(\frac{{\ v}_{z\left(t\right)}}{-g}\right)^2+z_{départ}$$
$$z\left(t\right)=-\frac{1}{2}g\frac{{{\ v}_{z\left(t\right)}}^2}{g^2}+z_{départ}$$
$$z\left(t\right)=-\frac{1}{2}\frac{{{\ v}_{z\left(t\right)}}^2}{g}+z_{départ}$$
$$z\left(t\right)=-\frac{1}{2} \times \frac{{307}^2}{9,66}+38\ 969$$
$$z\left(t\right)=34\ 090\ m$$
4. Indiquer, dans le cadre de ce modèle, en justifiant, si Felix Baumgartner a dépassé la vitesse du son lorsqu’il atteint cette altitude.
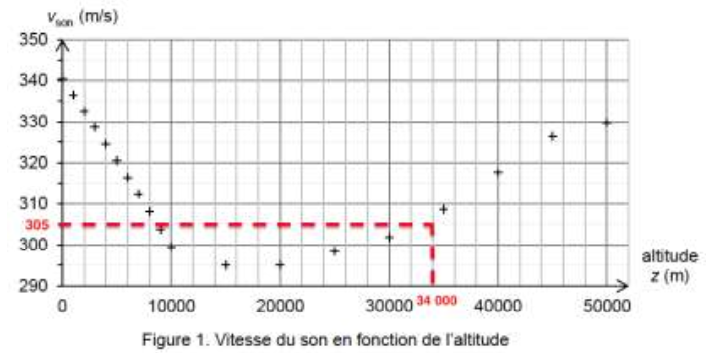
Trouvons graphiquement la vitesse du son pour l’altitude $z\left(t\right)=34\ 090\ m$
Pour $z\left(t\right)=34\ 090\ m$, $v_{son}=305\ m{.s}^{-1}.$
La vitesse de Félix Baumgartner est égale à 307 ms–1 pour cette altitude. Felix Baumgartner a donc dépassé la vitesse du son lorsqu’il atteint cette altitude.
Remarque : la détermination de la vitesse du son avec ce graphique est peu précise.
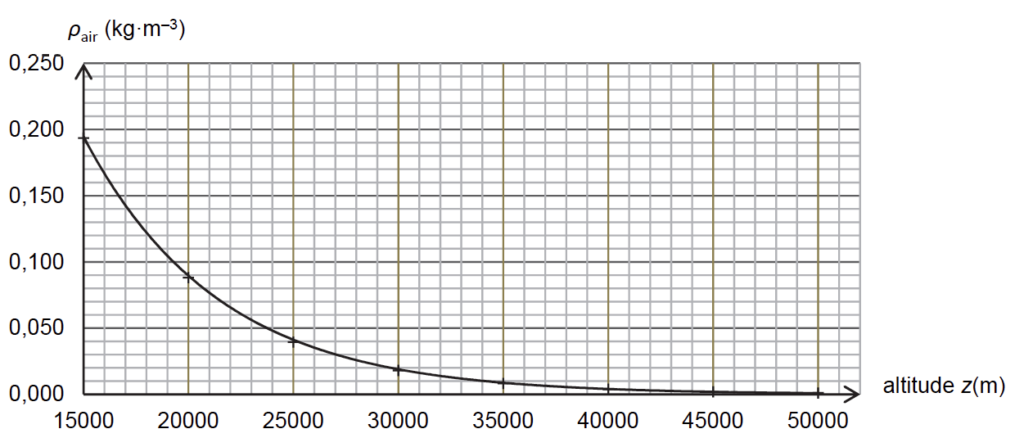
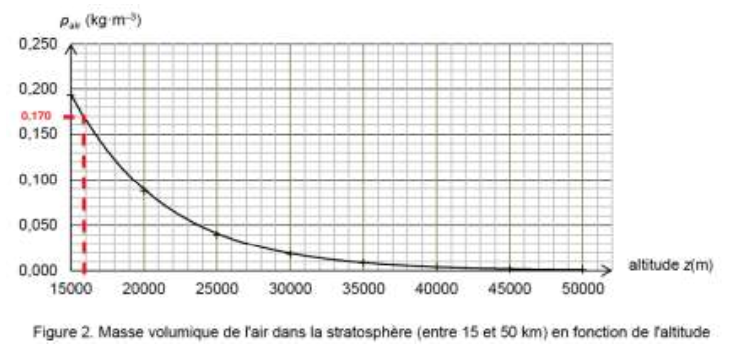
En réalité, Félix Baumgartner atteint une vitesse égale à celle du son à une altitude zson = 33 446 m. On donne, sur la figure 2 ci-dessous, l’évolution de la masse volumique ρair de l’air dans la stratosphère pour des altitudes comprises entre 15 km et 50 km.
5. Comparer la norme de la force de frottement de l’air et la norme du poids lorsque Félix Baumgartner atteint la vitesse de 307 m·s–1 à l’altitude de 33 446 m. Critiquer le modèle de chute libre utilisé précédemment.
Pour comparer la norme de la force de frottement de l’air et la norme du poids, on fait leur quotient :
$$\frac{P}{f}=\frac{m \times g}{0,4 \times \rho_{air}(z) \times v^2}$$
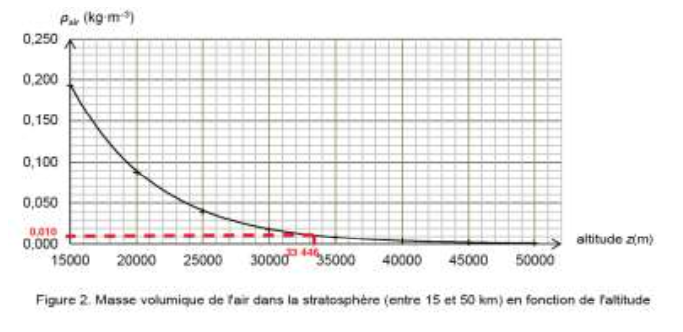
Graphiquement :
$$\rho_{air}\left(33\ 446\ \right)=0,010\ Kg{.m}^{-3}$$
$$\frac{P}{f}=\frac{120 \times 9,66}{0,4 \times 0,010 \times {307}^2}$$
$$\frac{P}{f}=3$$
Le poids est 3 fois plus grand que la force de frottement. Cependant la force de frottement n’est pas négligeable.
Nous ne sommes donc pas dans une chute libre.
En raison de la force de frottement due à l’air, Félix Baumgartner atteint une vitesse limite lors du saut. La vitesse limite est la vitesse atteinte lorsque la norme de la force de frottement devient égale à celle du poids.
6. Pour simplifier, on formule l’hypothèse que la vitesse limite est atteinte après 4 000 m de chute. Calculer la valeur de la vitesse limite vlim atteinte par Félix Baumgartner s’il s’était élancé d’une altitude z = 20 000 m.
D’après le texte : « La vitesse limite est la vitesse atteinte lorsque la norme de la force de frottement devient égale à celle du poids. »
f=P
$$0,4 \times \rho_{air}(z) \times v_{\lim}^2=m \times g$$
$$v_{\lim}^2=\frac{m \times g}{0,4 \times \rho_{air}(z)}$$
$$v_{lim}=\sqrt{\frac{m \times g}{0,4 \times \rho_{air}(z)}}$$
Félix Baumgartner s’il s’était élancé d’une altitude z = 20 000 m et la vitesse limite est atteinte après 4 000 m de chute. Soit $z=20\ 000-4000=16\ 000\ m$.
Graphiquement :
$$\rho_{air}\left(16\ 000\right)=0,170\ Kg{.m}^{-3}$$
$$v_{lim}=\sqrt{\frac{120 \times 9,66}{0,4 \times 0,170}}$$
$$v_{lim}=130\ m{.s}^{-1}$$
7. Expliquer qualitativement pourquoi il est nécessaire de s’élancer depuis la zone supérieure de la stratosphère pour atteindre une vitesse égale à celle du son.
Quel que soit l’altitude : $v_{son}>295\ m{.s}^{-1}$
Or depuis cette zone $v_{lim}=130\ m{.s}^{-1}<v_{son}$
Pour augmenter la vitesse, Il faut réduire les forces de frottements.
Or $f=0,4 \times \rho_{air}(z) \times v_{\lim}^2$
Pour réduire f il faut $\rho_{air}(z)$ soit plus faible.
Or $\rho_{air}(z)$ décroit avec l’altitude.
Ainsi est nécessaire de s’élancer depuis la zone supérieure de la stratosphère pour atteindre une vitesse égale à celle du son.
