Une exoplanète : 51PEG

Bac Amérique du nord 2022 Sujet 1

Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 22-PYCJ1AN1

EXERCICE C. UNE EXOPLANETE : 51PEG_b (5 POINTS)

Mots-clés : 3ème loi de Kepler dans le cas du mouvement circulaire, modèle optique d’une lunette astronomique.

En 2019, Michel Mayor et Didier Queloz obtiennent le prix Nobel pour la découverte en 1995 d’une exoplanète, nommée 51Peg_b, orbitant autour d’une étoile de type solaire, nommée 51Peg_a.

Données :

distance entre la Terre et l’étoile 51Peg_a : D_{Terre-51Peg_a} = 4,53 × 10¹⁷m ;
masse de l’étoile 51Peg_a : M_{51Peg_a} = 1,89 × 10³⁰ kg ;
masse du Soleil : M_Soleil = 1,989 × 10³⁰kg ;
constante de gravitation universelle : G = 6,6742 × 10^-11 m³∙s^-2∙kg^-1 .

A. Étude du système double 51Peg

Dans le cas du système double, constitué de l’exoplanète 51Peg_b et de son étoile 51Peg_a, les deux astres orbitent chacun autour du centre de masse B du système double. L’étoile 51Peg_a est animée d’un mouvement circulaire uniforme autour de B qui se manifeste par une variation de la coordonnée de son vecteur-vitesse selon l’axe de visée. Sur la figure suivante, le vecteur-vitesse de l’étoile est représenté par une flèche. Sa coordonnée selon l’axe de visée est : positive et maximale pour la position 1 ; nulle pour les positions 2 et 4 ; négative et minimale pour la position 3.

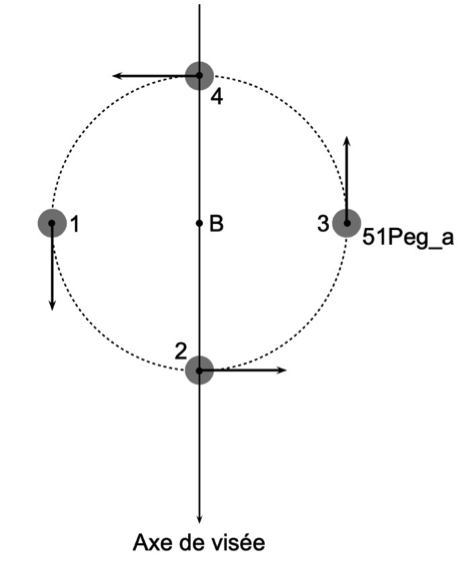
On détecte la variation de la coordonnée de ce vecteur-vitesse à travers l’effet induit sur le spectre lumineux de l’étoile. Cette coordonnée varie de façon périodique : la période correspond également à la période de révolution de l’exoplanète autour de son étoile.

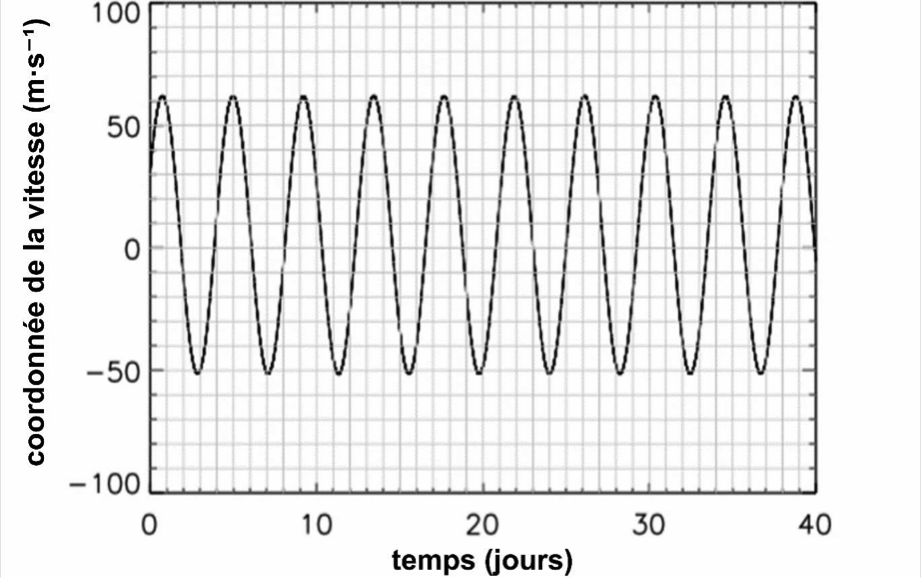
Source : ufe.obspm.fr

A.1. Mesurer, avec le plus de précision possible, la période de révolution T de l’exoplanète 51Peg_b autour de son étoile.

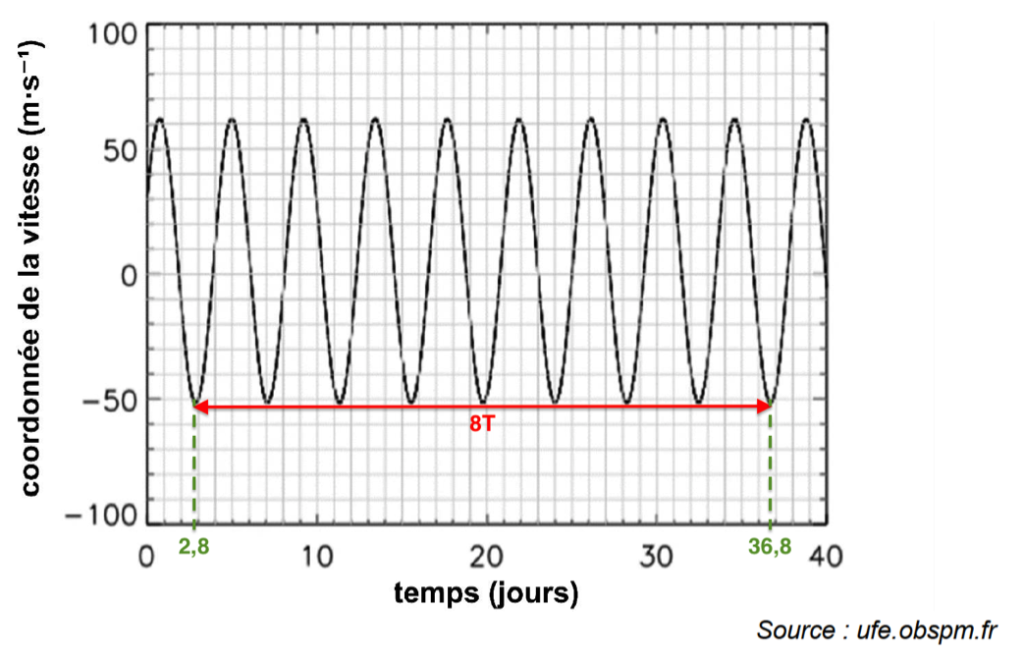
8T=36,8-2,8

8T=34

$T=\frac{34}{8}$

T=4,3 Jours

Le mouvement de 51Peg_b autour de son étoile est un mouvement circulaire uniforme vérifiant la troisième loi de Kepler. Par application de cette loi, on montre que la valeur de la distance r séparant la planète 51Peg_b de son étoile est égale à 7,5 × 10⁶ km.

A.2. Choisir, en argumentant, parmi les quatre expressions suivantes celle qui correspond à la troisième loi de Kepler pour la situation étudiée. L’argumentation devra s’appuyer notamment sur une analyse dimensionnelle.

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\bullet M_{51Peg_a}}$

$\frac{T^2}{r^3}=\frac{G\bullet M_{51Peg_a}}{4\pi ^2}}$

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\bullet M_{Soleil}}}$

$\frac{T^2}{r^3}=\frac{4\pi ^2G}{M_{51Peg_a}}$

Faisons une analyse dimensionnelle :

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\bullet M_{51Peg_a}}$

$\frac{\left[T\right]^2}{\left[r\right]^3}=\frac{\left[4\pi ^2\right]}{\left[G\right]\bullet \left[M_{51Peg_a}\right]}$

$\frac{s^2}{m^3}=\frac{1}{m^3\times s^{-2}\times Kg^{-1}\bullet Kg}$

$\frac{s^2}{m^3}=\frac{1}{m^3\times s^{-2}}$

$s^2\times m^{-3}=m^{-3}\times s^{2}$

La dimension est cohérente.

$\frac{T^2}{r^3}=\frac{G\bullet M_{51Peg_a}}{4\pi ^2}}$

$\frac{\left[T\right]^2}{\left[r\right]^3}=\frac{\left[G\right]\bullet \left[M_{51Peg_a}\right]}{\left[4\pi ^2\right]}$

$\frac{s^2}{m^3}=\frac{m^3\times s^{-2}\times Kg^{-1}\bullet Kg}{1}$

$\frac{s^2}{m^3}=m^3\times s^{-2}$

$s^2\times m^{-3}=m^3\times s^{-2}$

La dimension n’est pas bonne.

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\bullet M_{Soleil}}}$

$\frac{\left[T\right]^2}{\left[r\right]^3}=\frac{\left[4\pi ^2\right]}{\left[G\right]\bullet \left[M_{Soleil}\right]}$

$\frac{s^2}{m^3}=\frac{1}{m^3\times s^{-2}\times Kg^{-1}\bullet Kg}$

$\frac{s^2}{m^3}=\frac{1}{m^3\times s^{-2}}$

$s^2\times m^{-3}=m^{-3}\times s^{2}$

La dimension est cohérente.

$\frac{T^2}{r^3}=\frac{4\pi ^2G}{M_{51Peg_a}}$

$\frac{\left[T\right]^2}{\left[r\right]^3}=\frac{\left[4\pi ^2\right]\times \left[G\right]}{\left[M_{51Peg_a}\right]}$

$\frac{s^2}{m^3}=\frac{1 \times m^3\times s^{-2}\times Kg^{-1}}{Kg}$

$s^2\times m^{-3}= m^3\times s^{-2}\times Kg^{-2}$

La dimension n’est pas bonne.

Deux expressions sont possibles :

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\bullet M_{51Peg_a}}$

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\bullet M_{Soleil}}}$

Or le système étudié est : 51Peg_b qui gravite autour d’une étoile de type solaire, nommée 51Peg_a. La force qu’il subit est celle qu’exerce 51Peg_a. T²/R³ ne peut donc pas dépendre de M_Soleil.

Ainsi, la bonne expression qui correspond à la troisième loi de Kepler pour la situation étudiée est :

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\bullet M_{51Peg_a}}$

A.3. Retrouver la valeur de la distance r séparant la planète 51Peg_b de son étoile.

$\frac{T^2}{r^3}=\frac{4\pi ^2}{G\times M_{51Peg_a}}$

$\frac{r^3}{T^2}=\frac{G\times M_{51Peg_a}}{4\pi ^2}$

$r^3=\frac{G\times M_{51Peg_a}}{4\pi ^2}\times T^2$

$r=\sqrt[3]{\frac{G\times M_{51Peg_a}}{4\pi ^2}\times T^2}$

$r=\sqrt[3]{\frac{6,6742.10^{-11}\times 1,89.10^{30}}{4\pi ^2}\times \left(4,3\times 24\times 60\times 60\right)^2}$

$r=7,6.10^9\ m$

$r=7,6.10^6\ km$

Dans le système solaire, la planète Mercure est la plus proche du Soleil. Elle décrit une orbite quasi- circulaire de rayon égal à 5,8 × 10⁷ km en 88 jours.

A.4. Comparer les caractéristiques du système double constitué de l’exoplanète 51Peg_b et son étoile 51Peg_a à celles du système Mercure-Soleil.

$\frac{r_{Mercure}}{r_{51Peg_b}}=\frac{5,8.10^7}{7,73.10^6}=7,5$

Mercure est 7,5 fois plus éloignée du soleil que 51Peg_b de son étoile 51Peg_a.

$\frac{T_{Mercure}}{T_{51Peg_b}}=\frac{88}{4,3}=20$

La période de Mercure est 20 fois grande que celle de 51Peg_b.

B. La lunette astronomique et exoplanète

Le système exoplanétaire, constitué de l’étoile 51Peg_a et de son exoplanète 51Peg_b, est observé depuis la Terre.

On se pose la question de savoir s’il est possible de distinguer 51Peg_a et 51Peg_b à l’œil nu ou à travers une lunette pour astronome amateur.

L’œil peut distinguer deux objets si l’angle de séparation est au minimum de 3,0 × 10^-4 rad.

Angle de séparation entre deux objets lointains vus de la Terre

Pour des objets lointains, comme les étoiles, l’angle α qui sépare deux objets A et B vus de la Terre est donné par : α = AB/D . L’angle est exprimé en radian.

B.1. Indiquer si l’on peut distinguer 51Peg_a de 51Peg_b à l’œil nu.

$\alpha =\frac{AB}{D}$

AB: Distance entre 51Peg_a et 51Peg_b.

D: distance entre la Terre et l’étoile 51Peg_a

$\alpha =\frac{7,5.10^6\times 10^3}{4,53.10^{17}}$

$\alpha =1,7.10^{-8}\ rad$

$\alpha _{\min }=3,0.10^{-4}\ rad$

$\alpha <\alpha _{\min }$

Ainsi on ne peut pas distinguer 51Peg_a de 51Peg_b à l’œil nu.

Une lunette astronomique d’amateur est constituée d’un objectif de distance focale 𝑓′₁ égale à 900 mm et de plusieurs oculaires de distances focales 𝑓′₂ : 6,0 mm ; 10,0 mm ; 20,0 mm.

Un schéma de cette lunette astronomique se trouve sur le document réponse à rendre avec la copie (page 20/20).

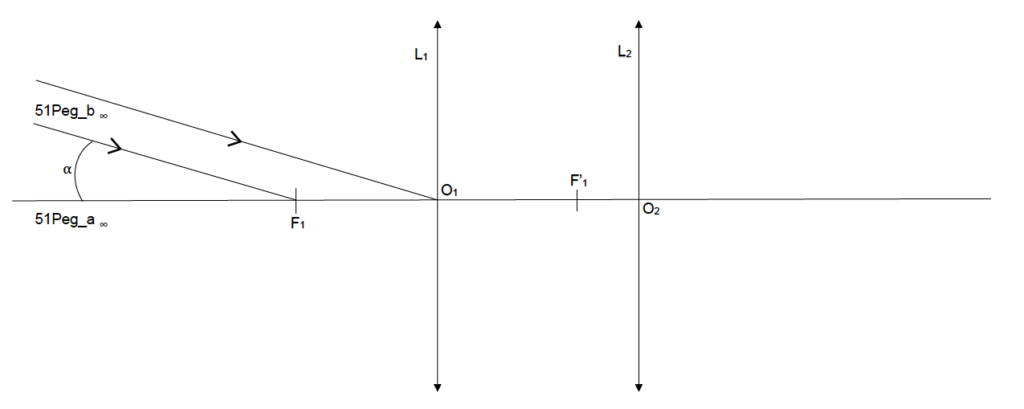
B.2. Compléter le schéma du document réponse à rendre avec la copie (page 20/20), avec le trajet de la lumière et faire apparaître l’angle 𝛼′ sous lequel est vu le système double quand on l’observe avec la lunette astronomique. On considère que l’étoile 51Peg_a est dans la direction de l’axe optique des lentilles de la lunette.

Le rayon lumineux 3 issu de 51Peg_b_∞ pénétrant dans la lunette par le centre optique O₁ de la lentille L₁ n’est pas dévié.

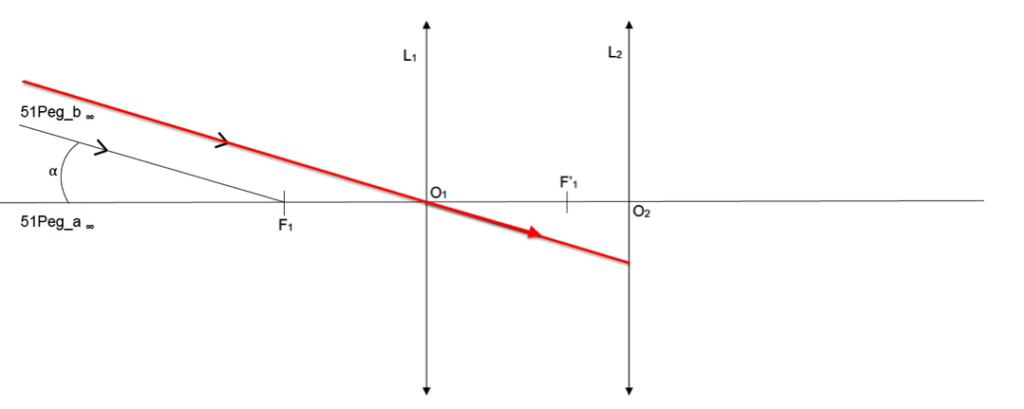
Le rayon lumineux 3 issu de 51Peg_b_∞ passant par F₁est dévié parallèlement à l’axe optique.

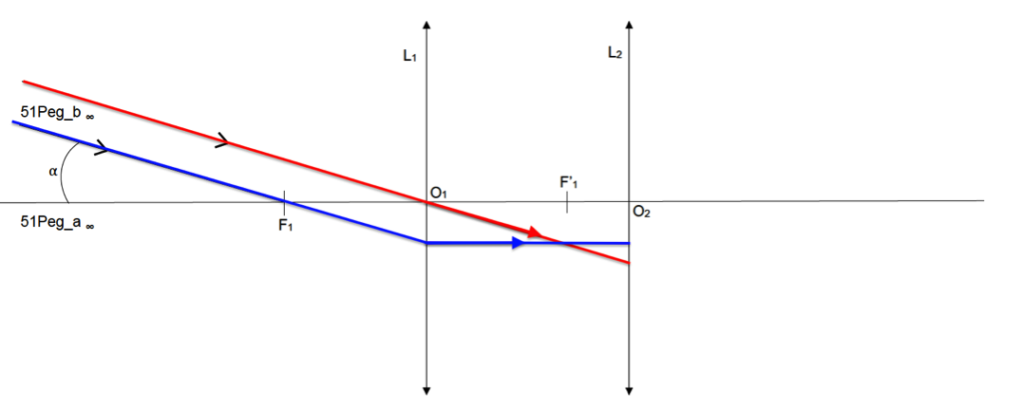
Position de B₁ image intermédiaire de 51Peg_b_∞ : intersection des deux rayons.

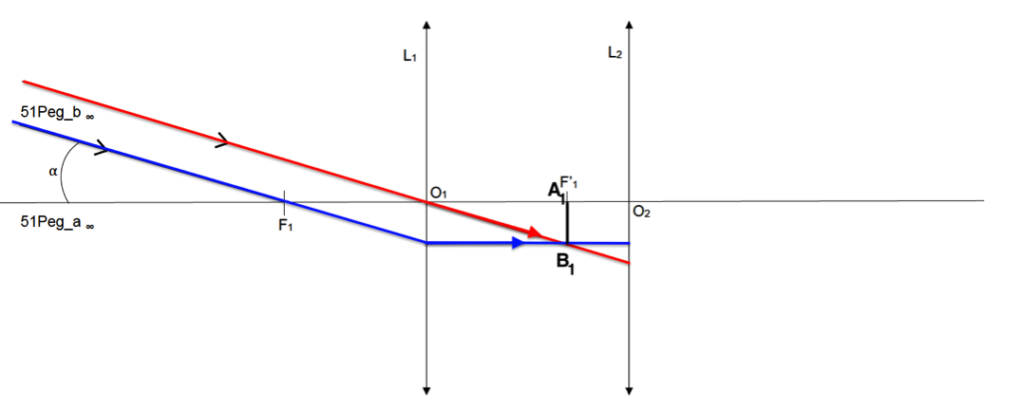
Remarque : on considère que la lunette est afocale F’₁ et F₂ sont confondus.

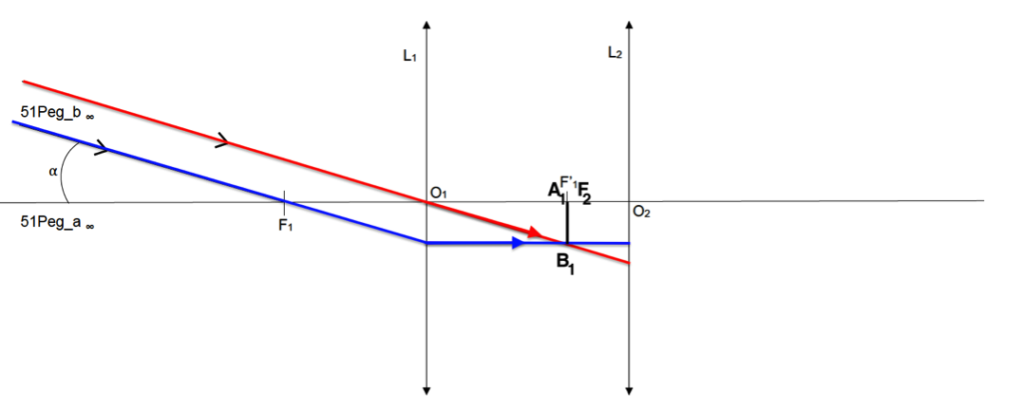
Pour les rayons émergeants de la lentille L₂ :

On trace un rayon issu de B₁ passant par O₂. Ce rayon ne sera pas dévié.
De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi les rayons émergeants de la lentille L₂ issue de B₁ seront parallèles à ce rayon tracé.

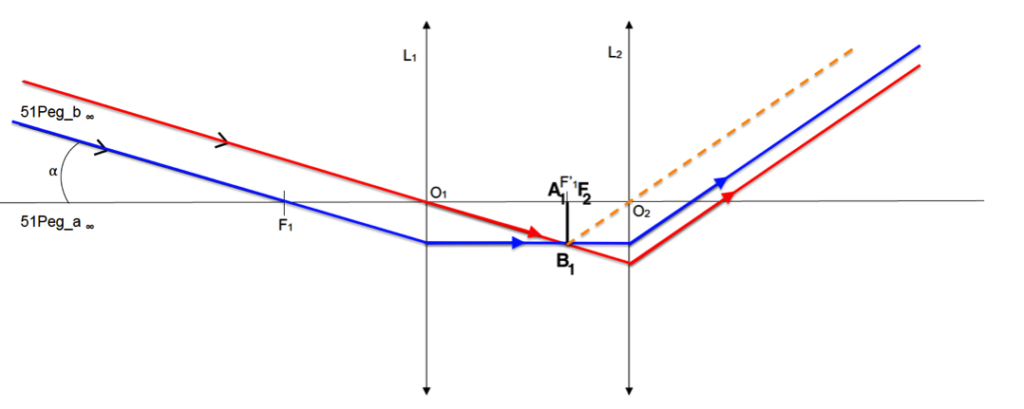
L’angle α’ sous lequel est vu le système double quand on l’observe avec la lunette astronomique

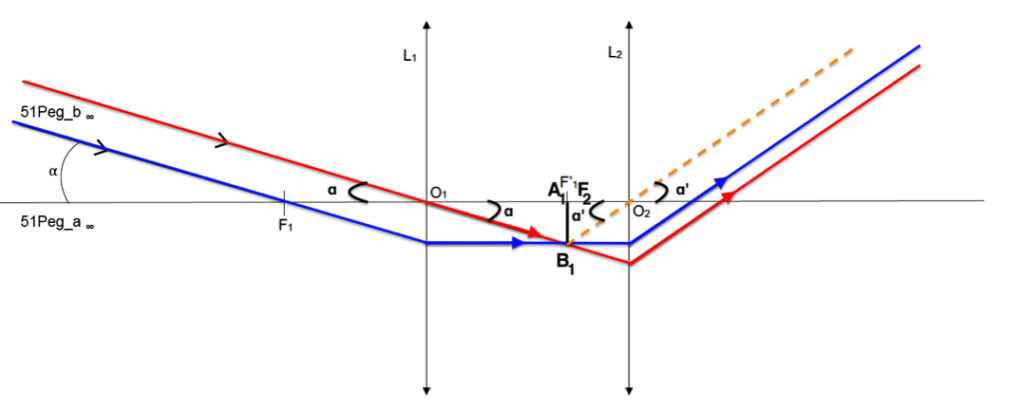
B.3. Établir l’expression du grossissement de la lunette en fonction de la distance focale de l’objectif et de la distance focale de l’oculaire.

$G=\frac{\alpha '}{\alpha }$

$\tan \left(\alpha \right)\approx \alpha =\frac{A_1B_1}{f_1^'}$

$G=\frac{\alpha '}{\alpha }=\frac{\frac{A_1B_1}{f_2^{'}}}{\frac{A_1B_1}{f_1^{'}}}=\frac{A_1B_1}{f_2^{'}}\times \frac{f_1^'}{A_1B_1}=\frac{f_1^'}{f_2^'}$

$G=\frac{f_1^'}{f_2^'}$

B.4. En détaillant le raisonnement, indiquer si l’on peut distinguer 51Peg_b de son étoile à l’aide du matériel disponible.

Pour pouvoir distinguer 51Peg_b de son étoile il faut un angle 𝛼′>𝛼_min avec 𝛼_min=3,0.10⁻⁴rad

Calculons 𝛼′ pour les différents oculaires :

$G=\frac{\alpha '}{\alpha }=\frac{f_1^'}{f_2^'}$

$\alpha '=\frac{f_1^'}{f_2^{'}}\times \alpha$

DOCUMENT REPONSE A RENDRE AVEC LA COPIE

Exercice C – Question B.2

Les échelles ne sont pas respectées.

21-PYCJ1AN1 20/20

Oculaires	𝛂′	Comparaison avec 𝛂_𝐦𝐢𝐧	Distinguer 51Peg_b de son étoile
6,0 mm	$\alpha '=\frac{f_1^{'}}{f_2^{'}}\times\alpha =\frac{900.10^{-3}}{6,0.10^{-3}}\times 1,7.10^{-8}=2,6.10^{-6}\ rad$	$\alpha ^{'}<\alpha _{\min }$	Non
10,0 mm	$\alpha '=\frac{f_1^{'}}{f_2^{'}}\times \alpha =\frac{900.10^{-3}}{10,0.10^{-3}}\times 1,7.10^{-8}=1,5.10^{-6}\ rad$	$\alpha ^{'}<\alpha _{\min }$	Non
20,0 mm	$\alpha '=\frac{f_1^{'}}{f_2^{'}}\times \alpha =\frac{900.10^{-3}}{20,0.10^{-3}}\times 1,7.10^{-8}=7,7.10^{-7}\ rad$	$\alpha ^{'}<\alpha _{\min }$	Non