Bac Asie 2021 Sujet 2
Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2JA1
Sujet et corrigé
Mots-clés : étude d’une lunette commerciale à partir d’un modèle, constructions graphiques, grossissement.
La notice d’une lunette astronomique commerciale pour amateur porte les indications suivantes :
- Lunette afocale
- Livrée avec deux oculaires de focales 6 mm et 12 mm
- Grossissement jusqu’à 100x
- Longueur totale 56 cm.
La valeur de la distance focale de l’objectif n’est pas précisée dans la notice.
On se propose de vérifier la cohérence de ces indications entre elles à l’aide d’une modélisation puis d’utiliser cette lunette commerciale pour encadrer la valeur de l’angle sous lequel se présente un système d’étoile double.
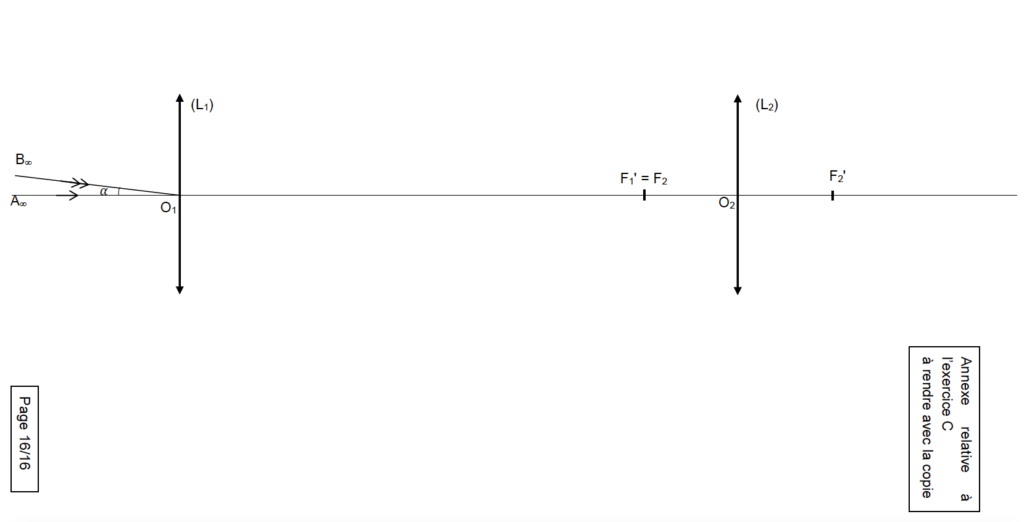
On modélise la lunette du commerce par deux lentilles minces convergentes (L1) et (L2) conformément au schéma en ANNEXE 2 page 16 / 16 à RENDRE AVEC LA COPIE.
- L’objectif est modélisé par une lentille (L1) convergente de centre optique O1 et de distance focale f1′.
- L’oculaire est modélisé par une lentille convergente (L2) de centre optique O2, et de distance focale f2′.
Le schéma n’est pas à l’échelle. Les lentilles (L1) et (L2) sont positionnées pour rendre le système afocal. On rappelle que pour un petit angle a exprimé en radians tan 𝛼 ≃ 𝛼.
Estimation de la valeur de la distance focale de l’objectif commercial à l’aide de la lunette modélisée
Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
1. En s’appuyant sur le schéma en ANNEXE 2 page 16 / 16 à RENDRE AVEC LA COPIE, justifier que la lunette modélisée est bien afocale.
« Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini. »
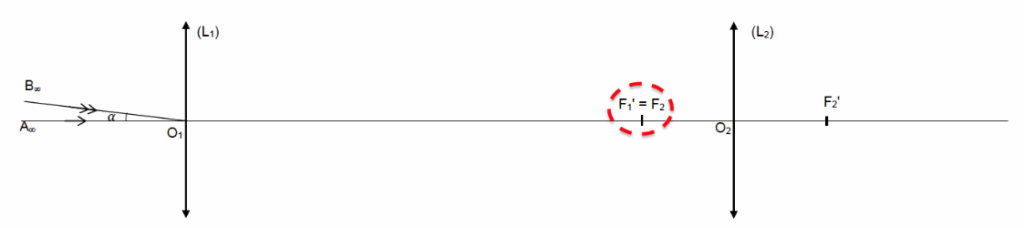
La lentille L1, donne de l’objet A∞ B∞, une image A1B1 sur le foyer image F’1.
Les deux foyers F’1 et F2 sont confondus, ainsi la lentille L2, donne de l’objet A1 B1, une image à l’infini.
La lunette est donc afocale.
2. Exprimer la distance O1O2 en fonction des distances focales f1′ et f2′ pour cette lunette afocale.
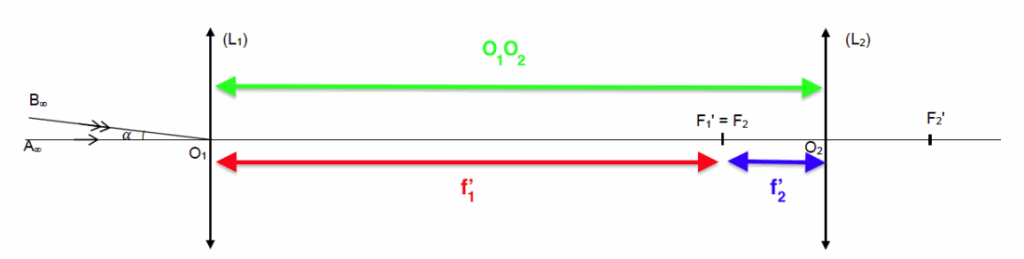
$$O_1O_2=f_1^\prime+f_2^\prime$$
3. À l’aide des indications commerciales, et en se basant sur le modèle étudié, montrer que la valeur de la distance focale de l’objectif de la lunette commerciale est de l’ordre de 55 cm.
$$f_1^\prime=O_1O_2-f_2^\prime$$
1er cas : $f_2^\prime=6\ mm$
$$f_1^\prime=O_1O_2-f_2^\prime$$
$$f_1^\prime=56 \times {10}^{-2}-6 \times {10}^{-3}$$
$$f_1^\prime=55 \times {10}^{-2}m=55cm$$
2nd cas : $f_2^\prime=12\ mm$
$$f_1^\prime=O_1O_2-f_2^\prime$$
$$f_1^\prime=56 \times {10}^{-2}-12 \times {10}^{-3}$$
$$f_1^\prime=55 \times {10}^{-2}m=55cm$$
Quel que soit le cas, $f_1^\prime=55cm.$
Estimation de la valeur du grossissement commercial
L’objet observé supposée à l’infini, est représenté sur le schéma en ANNEXE 2 page 16 / 16 à RENDRE AVEC LA COPIE par A∞B∞ (A∞ étant sur l’axe optique). Un rayon lumineux issu de B∞ est également représenté.
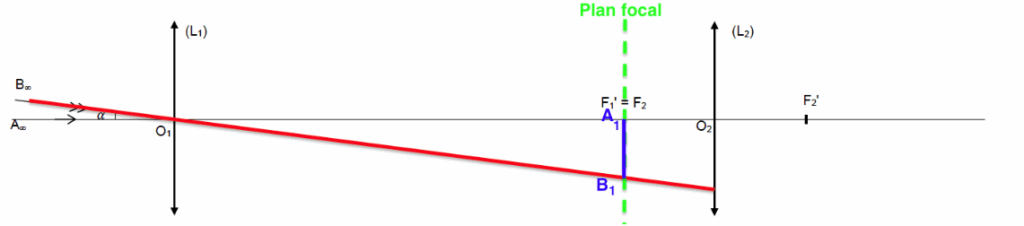
4. Sur le schéma en ANNEXE 2 page 16 / 16 à RENDRE AVEC LA COPIE, construire l’image A1B1 de l’objet A∞B∞, donnée par l’objectif.
La lentille L1, donne de l’objet $A_\inftyB_\infty$, une image $A_1B_1$ sur le plan focal.
Le rayon issu de B, passant par O1 n’est pas dévié.
Le point B1 est défini par l’intersection de ce rayon et le plan focal.
On désigne par 𝛼 le diamètre apparent de l’objet, c’est-à-dire l’angle sous lequel on voit l’objet à l’œil nu. On a représenté 𝛼 sur le schéma de l’annexe.
5. Exprimer tan 𝛼 en fonction de f1′ et A1B1 .
$$tan\left(\propto\right)\approx\propto=\frac{A_1B_1}{f_1^\prime}$$
L’oculaire (L2) permet d’obtenir une image définitive A′B′ perçue par l’œil sous un angle 𝛼′.
6. Sur le schéma en ANNEXE 2 page 16 / 16 à RENDRE AVEC LA COPIE, construire la marche d’un rayon lumineux incident issu de B1 émergent de la lentille (L2).
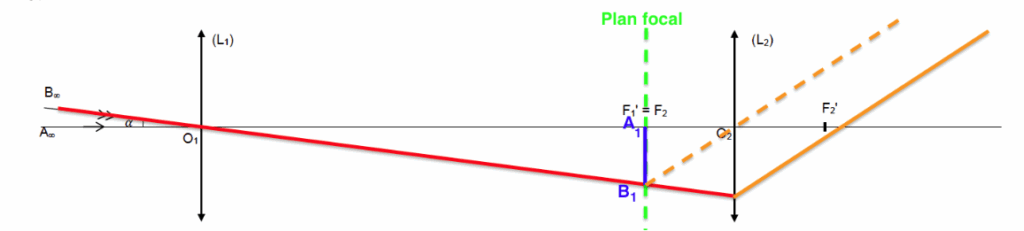
Un rayon issu de B1 passant par O2 n’est pas dévié.
$A_1B_1$ étant sur le plan focal, il donnera une image à l’infini, tous les rayons issus de B1, passant par la lentille L2 seront parallèles.
7. Positionner 𝛼′ sur le schéma et exprimer tan 𝛼′ en fonction de f2′ et A1B1 .
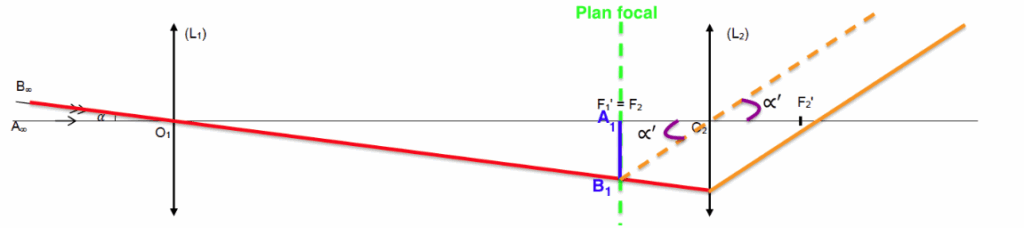
$$tan\left(\propto^\prime\right)\approx\propto^\prime=\frac{A_1B_1}{f_2^\prime}$$
8. Rappeler la définition du grossissement G de la lunette et l’exprimer en fonction des distances focales f1′ et f2′.
$$G=\frac{\propto^\prime}{\propto}=\frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}}=\frac{A_1B_1}{f_2^\prime} \times \frac{f_1^\prime}{A_1B_1}=\frac{f_1^\prime}{f_2^\prime}$$
9. Justifier l’intérêt d’utiliser des lentilles telles que .
Si on utilise des lentilles telles que f2′≪ f1′ , alors $\frac{f_1^\prime}{f_2^\prime}=G\gg1$ , ainsi le grossissement G sera grand.
10. Compte tenu de la valeur de la distance focale de l’objectif de la lunette commerciale estimée à la question 3, discuter de la cohérence de l’indication « Grossissement jusqu’à 100 × » et préciser si d’autres valeurs du grossissement sont également possibles pour cette lunette commerciale.
$$G=\frac{f_1^\prime}{f_2^\prime}$$
1er cas : $f_2^\prime=6\ mm$
$$G=\frac{f_1^\prime}{f_2^\prime}$$
$$G=\frac{55 \times {10}^{-2}}{6 \times {10}^{-3}}=92$$
L’indication « Grossissement jusqu’à 100 × » n’est pas totalement vraie bien que le grossissement soit de l’ordre de grandeur d’une centaine de fois.
2nd cas : $f_2^\prime=12\ mm$
$$G=\frac{f_1^\prime}{f_2^\prime}$$
$$G=\frac{55 \times {10}^{-2}}{12 \times {10}^{-3}}=46$$
Cette lunette commerciale propose également un grossissement de 46 fois.
Observation d’étoiles doubles
Certaines étoiles apparaissent si proches l’une de l’autre qu’il est souvent impossible de les distinguer à l’œil nu pour un observateur sur Terre.

photographiées à l’aide
d’un télescope
Données :

L’œil humain ne peut distinguer deux points A et B que si l’angle 𝜃 sous lequel sont vus les deux points est supérieur à 3,0 × 10–4 rad.
On observe un système d’étoiles doubles à travers la lunette commerciale. Avec l’un des deux oculaires fournis, on observe un point lumineux unique tandis qu’avec l’autre on observe deux points lumineux.
11. Préciser les oculaires utilisés pour chaque observation et donner un encadrement de l’angle 𝛼 sous lequel se présentent les deux étoiles à l’œil nu.
Le candidat est invité à prendre des initiatives et à présenter sa démarche. Toute démarche, même non aboutie, sera valorisée.
« Avec l’un des deux oculaires fournis, on observe un point lumineux unique » c’est le plus petit grossissement qui est utilisé soit G=46 donc l’oculaire f_2^\prime=12\ mm.
« Tandis qu’avec l’autre on observe deux points lumineux. », c’est le plus grand grossissement qui est utilisé soit G=92 donc l’oculaire f_2^\prime=6\ mm .
$$G=\frac{\propto^\prime}{\propto}$$
$$\propto=\frac{\propto^\prime}{G}$$
1er cas : G=46
$$\propto=\frac{\propto^\prime}{G}$$
$$\propto=\frac{3,0 \times {10}^{-4}\ }{46}$$
$$\propto=6,5 \times {10}^{-6} rad$$
2nd cas : G=92
$$\propto=\frac{\propto^\prime}{G}$$
$$\propto=\frac{3,0 \times {10}^{-4}\ }{92}$$
$$\propto=3,3 \times {10}^{-6} rad$$
D’ou
$$3,3 \times {10}^{-6}rad\ <\propto<6,5 \times {10}^{-6} rad$$
ANNEXE 1 relative à l’exercice 1 à RENDRE AVEC LA COPIE