E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02712
Télécharger l’exercice en PDF :
Le cobra est un serpent qui a la capacité de se redresser. C’est en référence à cette position que le jeu étudié ici a été nommé « onde cobra ». Il ressemble à ce jeu dans lequel on aligne des milliers de dominos pour ensuite les faire tomber en cascade.
Il s’agit ici d’entremêler en une succession de losanges des bâtonnets de bois, par exemple des bâtonnets de glace, pour constituer un long croisillon horizontal puis d’en lâcher une extrémité.

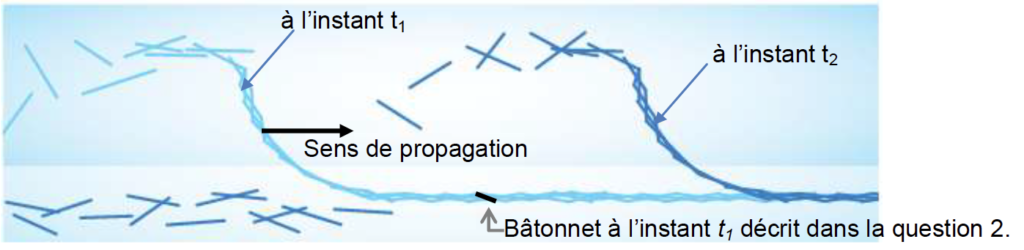
L’assemblage se soulève alors, se redresse telle une tête de cobra, en éjectant un à un les bâtonnets et en détruisant donc le croisillon (figure 1 ci-dessous).
Pour constituer le croisillon (figure 2 ci-dessous), les bâtonnets se déforment avec des fléchissements qui sont de l’ordre de leur épaisseur (figure 3 ci-dessous), mais qui retrouvent leur forme initiale une fois libérés. Initialement, ils stockent ainsi non pas de l’énergie potentielle de pesanteur mais de l’énergie potentielle élastique. Des chercheurs ont montré que l’onde cobra résultait d’une propulsion par réaction, dans laquelle le « carburant » est cette énergie potentielle élastique stockée dans les déformations des bâtonnets et la propagation est assurée par leur éjection.
L’objectif de cet exercice est de déterminer la célérité de l’onde cobra, d’étudier l’influence de la forme du croisillon sur la célérité ainsi que de mener une analyse énergétique pour interpréter l’onde cobra et prévoir la hauteur maximale des bâtonnets lors de la propagation.
Sources : journal Le Monde (21 août 2017), journal Pour la Science (n°490, août 2018).

Figure 2 : Croisillon vu de dessus : le croisillon est caractérisé par le pas noté p, distance entre deux sommets consécutifs sur un des bords du croisillon


Figure 3 : Schéma de profil d’un bâtonnet déformé dans le croisillon et photo correspondante
Analyse ondulatoire
1. Indiquer la nature périodique ou non périodique de « l’onde cobra ».
L’onde cobra est non périodique. La perturbation ne se reproduit pas identique à elle-même à intervalles de temps égaux.
2. On souhaite décrire l’évolution de la hauteur du centre de masse d’un bâtonnet au cours du temps (la hauteur est nulle lorsque le bâtonnet est au sol). Le bâtonnet décrit est figuré en noir à l’instant t1 sur la figure 1, lorsqu’il est encore au sol, et on peut considérer que son mouvement ultérieur est approximativement vertical. Quatre représentations graphiques sont proposées ci-dessous.
2.1. Parmi les représentations graphiques proposées, éliminer la (ou les) représentation(s) qui ne rend(ent) pas compte de la position du bâtonnet à l’instant t1.
« Le bâtonnet décrit est figuré en noir à l’instant t1 sur la figure 1, lorsqu’il est encore au sol ».
Les représentations a et d ne rendent pas compte de la position du bâtonnet à l’instant t1.
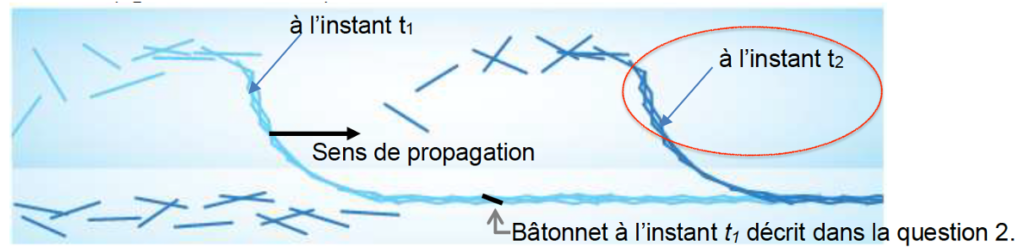
2.2. Parmi les représentations restantes, choisir la représentation graphique qui paraît la plus adaptée. On justifiera clairement le choix.
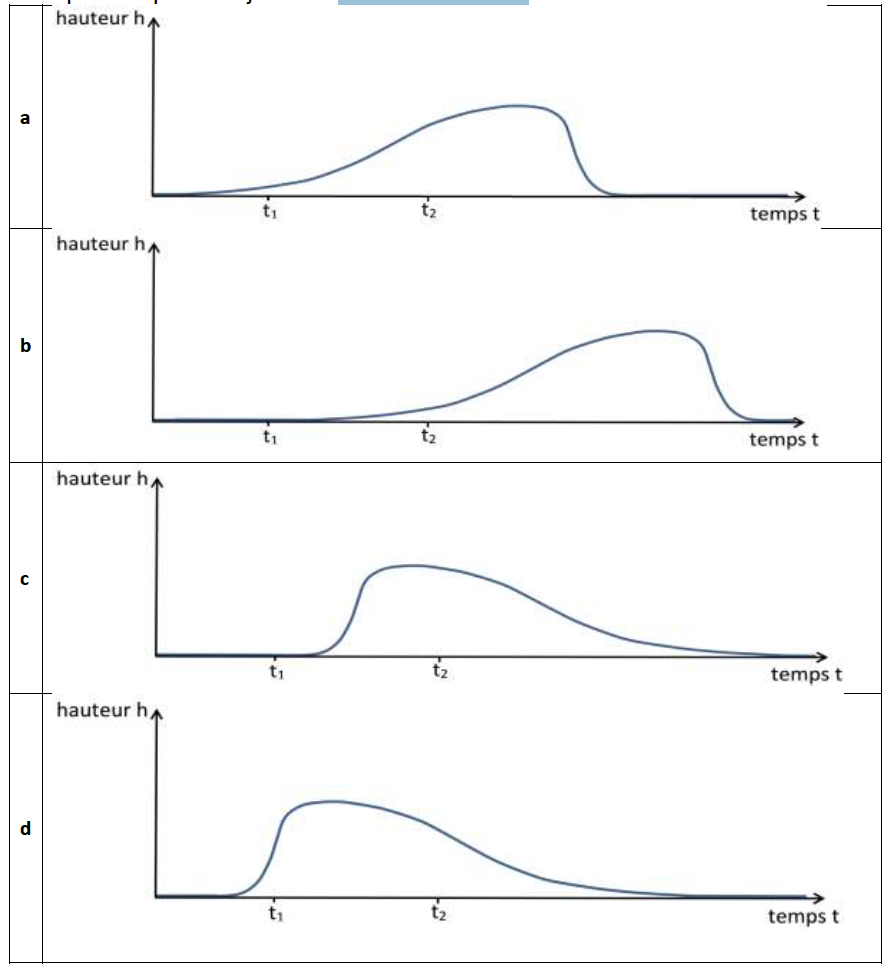
Sur le graphique de la figure 1, à l’instant t2, le bâtonnet n’est plus au sol.
Ainsi la représentation c parait la plus adaptée.
Des chercheurs ont réalisé des photographies successives de la structure se soulevant au cours du temps. Quatre photographies successives sont fournies sur la figure 4 ci-dessous. Le croisillon a été réalisé avec des bâtonnets de longueur 11,4 cm et un pas voisin de 5 cm (ce qui correspond à des bâtonnets disposés perpendiculairement les uns par rapport aux autres comme sur la figure 2). L’échelle verticale et l’échelle horizontale ne sont pas les mêmes.
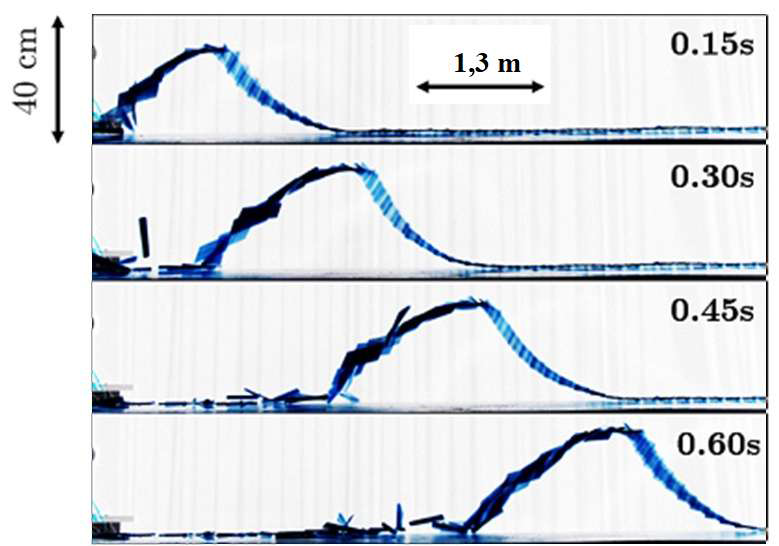
Figure 4 : Photographies successives de la structure.
D’après : Jérémy Sautel, Andréane Bourges, Aude Caussarieu, Nicolas Plihon, and Nicolas Taberlet The physics of a popsicle stick bomb American Journal of Physics 85, 783 (2017)
3. À l’aide de la figure 4, justifier sans calcul que la célérité de l’onde cobra semble approximativement constante.
On remarque que pour intervalles de temps égaux, l’onde se déplace d’une distance quasiment constante. Ainsi la célérité de l’onde cobra semble approximativement constante.
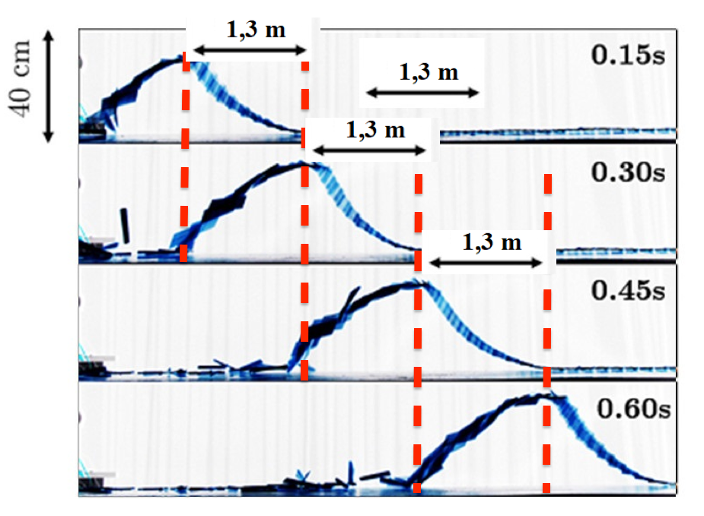
4. Déterminer la valeur de la célérité de l’onde cobra. On explicitera clairement la méthode.
La distance parcourue est d=1,3m entre chaque image.
L’intervalle de temps $\Delta t=0,15\ \text{s}$ entre chaque image.
v=d$\Delta t$
$v=\frac{1,3}{0,15}=8,7\ m.s^{-1}$
L’évolution de la célérité de l’onde et de la hauteur maximale atteinte par chaque bâtonnet en fonction du pas sont reproduites ci-dessous (pour des bâtonnets de longueur 11,4 cm). Les barres indiquent l’incertitude-type pour chaque mesure.
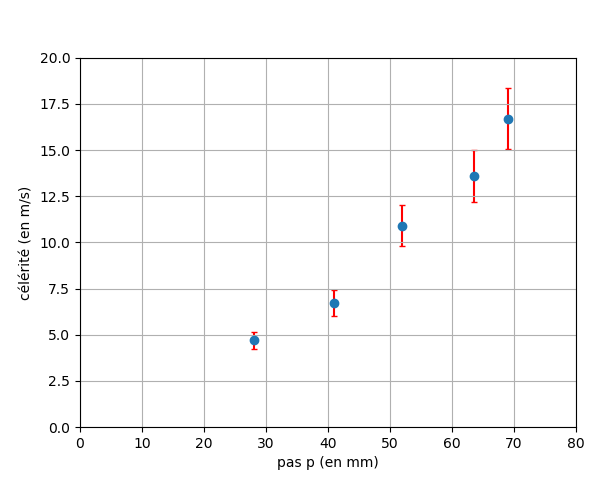
Figure 5 : célérité en fonction du pas
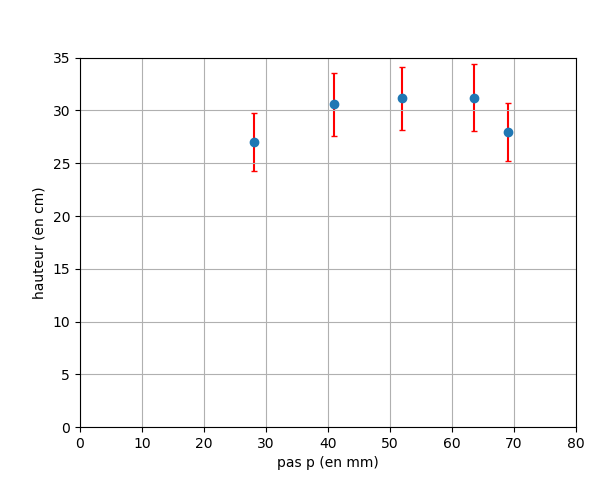
Figure 6 : hauteur maximale en fonction du pas
5. Indiquer comment on a intérêt à déformer le croisillon afin d’augmenter la vitesse par rapport à la situation étudiée aux questions 3 et 4. On pourra faire un schéma.
Lorsque le pas p augmente, la vitesse augmente (figure5).
Ainsi, pour augmenter la vitesse augmente, il faut augmenter le pas.
Figure 2 « Le pas noté p, distance entre deux sommets consécutifs sur un des bords du croisillon ».
Il faut donc augmenter la distance entre deux sommets consécutifs sur un des bords du croisillon.
6. Indiquer en argumentant avec précision si la forme du croisillon a une influence sur la hauteur atteinte par les bâtonnets.
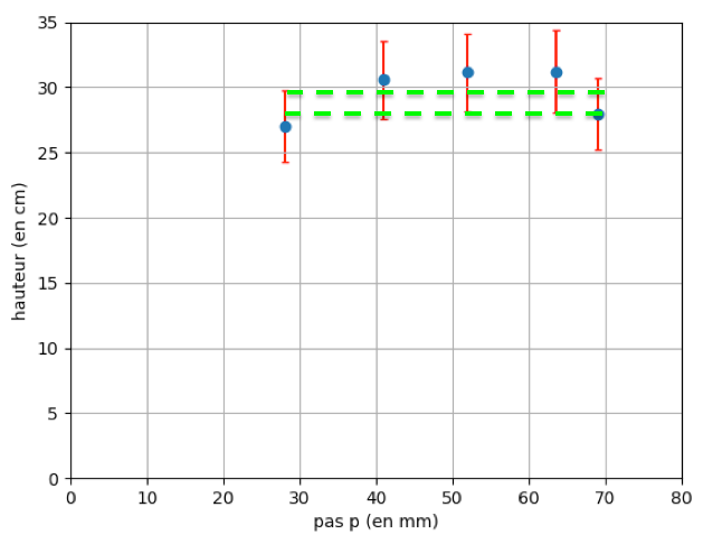
Sur la figure 6 nous remarquons que la hauteur moyenne est constante et maximale pour un pas compris entre 40 et 65 mm. Elle est légèrement plus faible pour un pas inferieur ou supérieur.
Cependant, l’incertitude-type nous montre que toutes les mesures se chevauchent. Ainsi nous pouvons dire que la forme des croisillons n’a pas d’influence sur la hauteur atteinte par les bâtonnets.
Analyse énergétique
On souhaite estimer l’énergie nécessaire à la déformation d’un bâtonnet dont les caractéristiques figurent dans les données ci-dessous. Pour ceci, on étudie la situation suivante où on pose deux masselottes identiques à chaque extrémité d’un bâtonnet fixé en son centre. Celui-ci se courbe et stocke de l’énergie potentielle élastique. On note M la masse de chacune des masselottes pour que les extrémités du bâtonnet descendent d’une hauteur égale à son épaisseur. Pour déformer à ses deux extrémités le bâtonnet décrit dans les données, on observe expérimentalement qu’il faudrait que les masselottes aient chacune une masse M environ égale à 100 g.

Données :
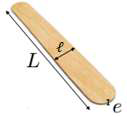
- dimensions d’un bâtonnet :
longueur : L = 15,0 cm ;
largeur : ℓ = 2,8 cm ;
épaisseur : e = 1,6 mm ;
- masse d’un bâtonnet : m = 2,5 g ;
- intensité du champ de pesanteur : g = 9,8 m·s-2.
7. Exprimer le travail du poids d’une masselotte durant sa descente. Calculer sa valeur.
$W_{AB}(\overrightarrow{P})=M\times g\times(Z_A-Z_B)$
La masselotte descend d’environs une épaisseur $e$ : $Z_A-Z_B=e$

$W_{AB}(\overrightarrow{P})=M\times g\times e$
$W_{AB}(\overrightarrow{P})=100.10^{-3}\times 9.8\times 1.6.10^{-3}$
$W_{AB}(\overrightarrow{P})=1,6.10^{-3}\ J$
On suppose que l’énergie transférée par travail mécanique est entièrement stockée par le bâtonnet sous forme d’énergie potentielle élastique.
8. En déduire la valeur de l’énergie potentielle élastique d’un bâtonnet qui serait déformé de cette façon par les deux masselottes avec un fléchissement égal à son épaisseur à chaque extrémité.
$E_{pe}=2\times W_{AB}(\overrightarrow{P})$
$E_{pe}=2\times1.6.10^{-3}$
$E_{pe}=3,2.10^{-3}\ J$
En pratique, puisque chaque bâtonnet est déformé en quatre points, l’énergie potentielle stockée par bâtonnet est bien plus grande et vaut approximativement 50 mJ.
L’énergie mécanique d’un bâtonnet est la somme de son énergie cinétique, de son énergie potentielle de pesanteur (considérée nulle lorsque le bâtonnet est au sol) et de son énergie potentielle élastique (nulle lorsque le bâtonnet n’est pas déformé). Lors de la propagation de l’onde, chaque bâtonnet est propulsé vers le haut et n’est plus déformé. Lorsqu’il atteint sa hauteur maximale, on peut considérer sa vitesse comme nulle.
9. En exploitant la conservation de l’énergie mécanique pour un bâtonnet donné, exprimer puis calculer la valeur de la hauteur maximale théorique atteinte par chaque bâtonnet.
L’élève est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
L’énergie mécanique se conserve :
Em(haut)=Em(sol)
Epp(haut) + Ec(haut) + Epe(haut)= Epp(sol) + Ec(sol) + Epe(sol)
Or
Ec(haut)=0J car la vitesse est nulle au point le plus haut
Epe(haut)= 0J car le bâtonnet n’est plus déformé
Epp(sol)=0J car la hauteur est nulle
Ec(sol)=0J car la vitesse est nulle au niveau du sol.
Ainsi :
Epp(haut) = Epe(sol)
m×g×h = Epe(sol)
$h=\frac{E_{pe}(\text{sol})}{m\times g}$
$h=\frac{50.10^{-3}}{2,5.10^{-3}\times9,8}=2,0\ m$
Lors de la propagation observée expérimentalement, la hauteur atteinte par chaque bâtonnet est comprise entre 25 et 35 cm.
10. Proposer une interprétation de la différence avec la valeur calculée précédemment.
La différence peut s’expliquer par :
- La vitesse au point le plus haut n’est pas nulle
- L’énergie mécanique ne se conserve pas du fait des frottements.
