Liban 2022 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1LR1
Sujet et corrigé
Mots-clés : mouvement dans un champ de pesanteur uniforme, énergie mécanique ; lecture d’un programme écrit en langage Python.
Des chercheurs ont développé une table de tennis de table connectée qui permet d’identifier les points de chute d’une balle et de déterminer sa vitesse lorsqu’elle touche la table. L’analyse des données peut être utilisée pour améliorer la performance des joueurs.
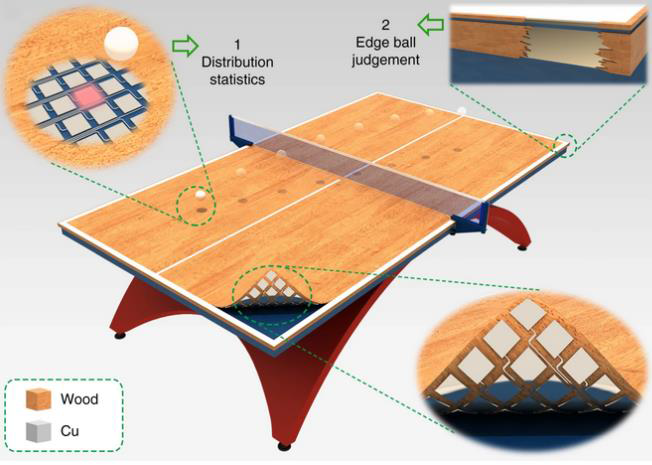
https://www.nature.com/articles/s41467-019-13166-6
Caractéristiques des capteurs de vitesse
La table connectée est équipée de capteurs qui convertissent les contraintes mécaniques reçues en tension électrique. Ces capteurs ont une surface sensible carrée d’environ 4 cm de côté. Lorsqu’une balle rebondit sur la surface sensible, un capteur horizontal délivre une tension variable dans le temps dont la valeur maximale U dépend de la valeur de la composante verticale de la vitesse que la balle possède juste avant de rentrer en contact avec le capteur.
Dans une étude expérimentale où le capteur est horizontal et où la verticale ascendante est la direction de l’axe Oy, on obtient les résultats résumés par le graphique suivant, où |vy| est la valeur absolue de la composante vy de la vitesse avant l’impact.
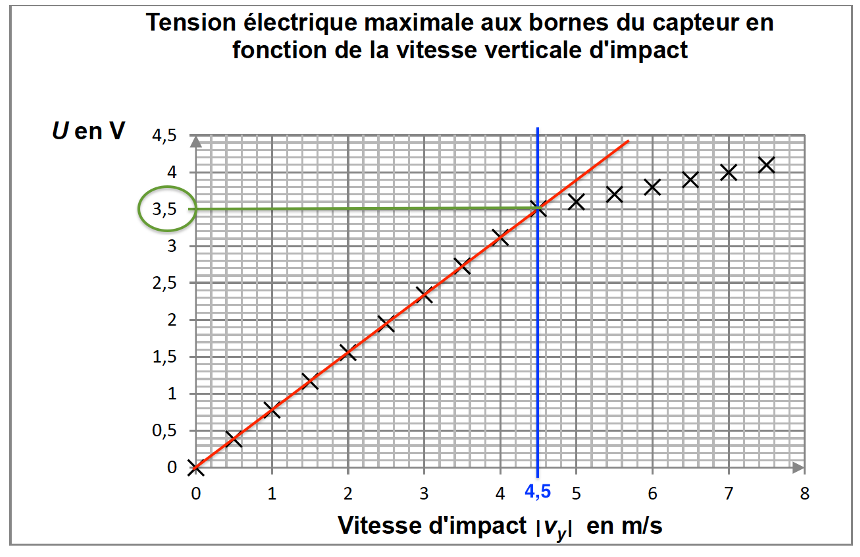
Tension électrique maximale aux bornes du capteur en fonction de la vitesse verticale d’impact
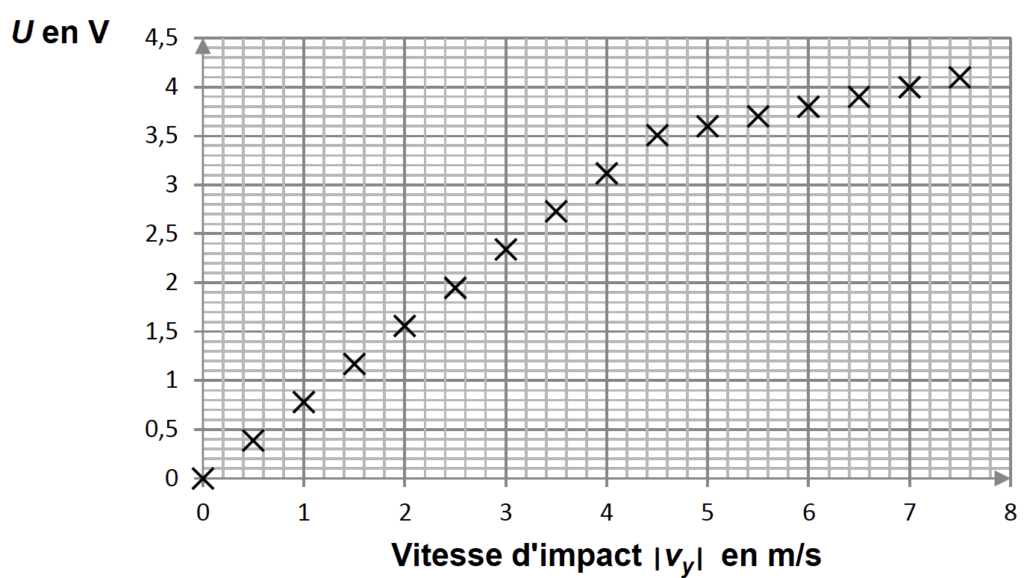
1. Justifier que pour des vitesses d’impact |vy| inférieures à 4,5 m·s-1, la tension électrique U est proportionnelle à |vy|. En déduire dans ce domaine de vitesses la relation entre |vy| et U avec |vy| exprimée en m·s-1 et U en V.
Graphiquement on a une droite passant par l’origine pour des vitesses d’impact |vy| inférieures à 4,5 m·s-1.
Ainsi, la tension électrique U est proportionnelle à |vy| pour des vitesses d’impact |vy| inférieures à 4,5 m·s-1.
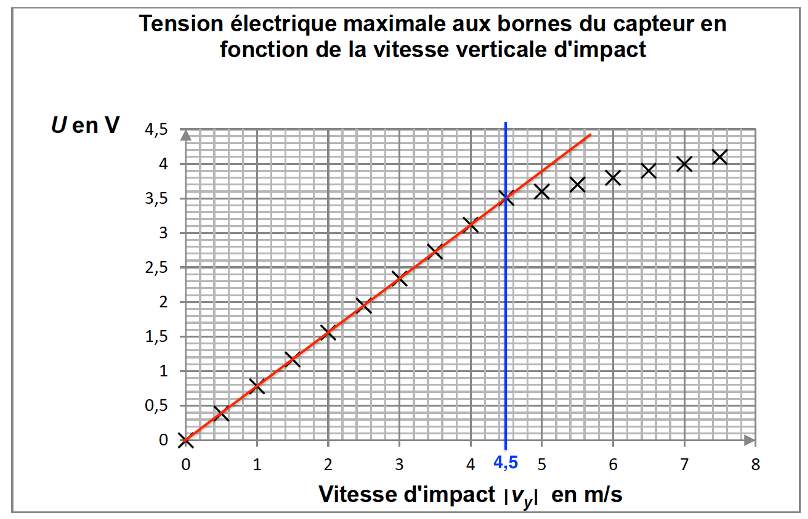
$$k=\frac{y_B-y_A}{x_B-x_A}$$
$$k=\frac{3{,}5-0}{4{,}5-0}$$
$$k=0{,}78\ \text{m·s}^{-1}\text{·V}^{-1}$$
D’ou
$$U=0{,}78 \times |v_y|$$
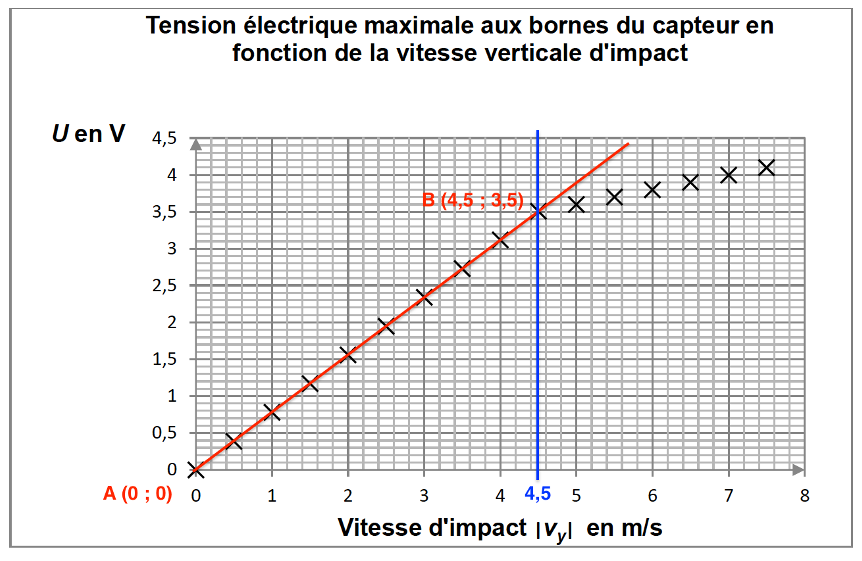
Un exemple de programme Python permettant l’affichage de la vitesse d’impact verticale à partir de la tension U est proposé ci-dessous :
# U est la tension maximale aux bornes du capteur en V
# v est la valeur absolue de la composante vy de la vitesse avant l’impact, en m/s.
Ulim = 3.5
if U < Ulim:
v = 1.3*U
else:
v = 5,0*U–13
print(« La vitesse d’impact est »,v,« en m/s »)
2. Expliquer la nécessité d’utiliser la variable « Ulim = 3.5 » dans le programme informatique.
La relation de proportionnalité est valable pour des vitesses d’impact |vy| inférieures à 4,5 m·s-1 soit jusqu’à U=3,5V.
D’où « Ulim = 3.5 »
3. Calculer la valeur de la vitesse d’impact affichée par ce programme pour une tension U de 4,0 V. Comparer la valeur calculée à la valeur mesurée correspondante.
Pour une tension $U$ de $4{,}0\ \text{V}$ :
$$v=5{,}0 \times U-13$$
$$v=5{,}0 \times 4{,}0-13$$
$$v=7\ \text{m·s}^{-1}$$
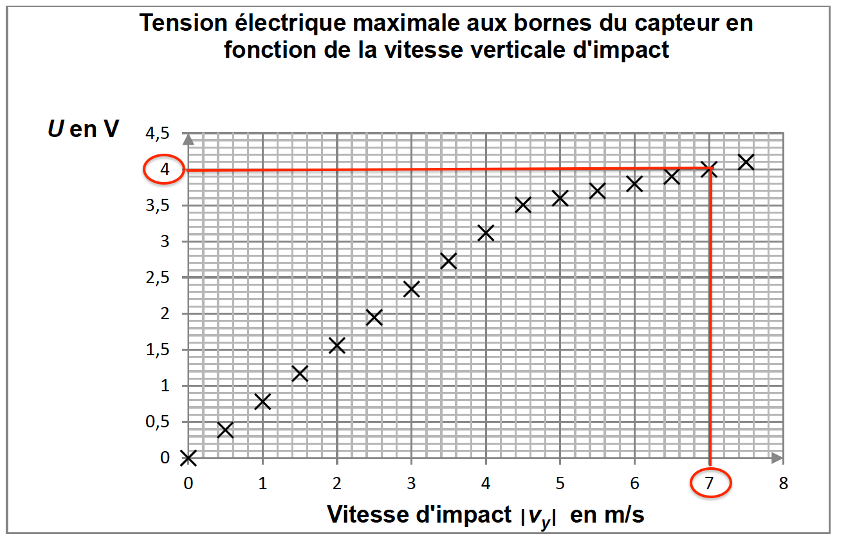
La valeur trouvée est la même que la valeur mesurée.
Exemple d’utilisation
On étudie le mouvement d’une balle de ping pong (tennis de table) de masse m = 2,7 g qui évolue dans le champ de pesanteur terrestre supposé uniforme. On néglige l’action de l’air.
L’étude du mouvement de la balle est réalisée dans le référentiel terrestre, supposé galiléen, dans lequel on choisit un repère (O;x;y) où la verticale ascendante est parallèle à l’axe Oy. La table est dans le plan y = 0. Le point O est au bord de la table et l’axe Ox est parallèle au grand côté de la table dont la longueur est 2,74 m.
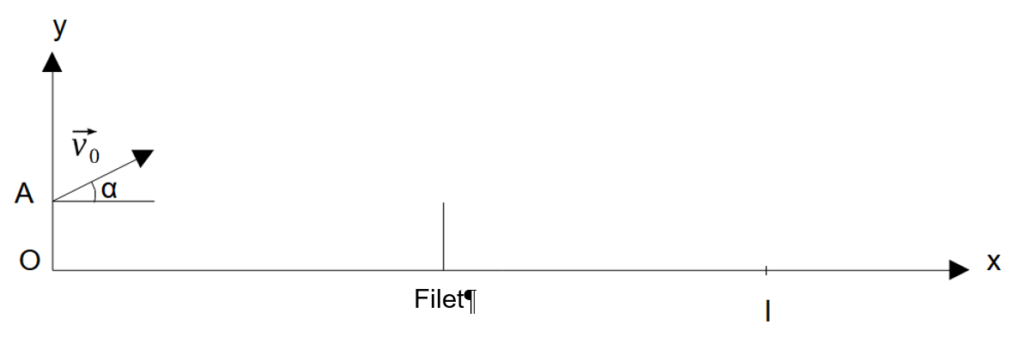
À la date t = 0 s, la balle est située au point A sur la verticale de O à la hauteur h = OA = 0,10 m. La balle part du point A avec une vitesse v0 = 5,0 m.s-1 faisant un angle α = 30,0 ° avec l’horizontale. À la date tI, elle touche la table au point d’impact I de coordonnées (xI ;0).
Le document 1, tracé sans souci d’échelle, schématise la situation.
Représentation schématique du problème
Donnée
valeur du champ de pesanteur terrestre : g = 9,8 m·s-2.
4. La balle de ping pong est une sphère de diamètre d = 40 mm. On étudie le mouvement de son centre de masse, localisé au centre de la sphère. Justifier qualitativement la position de ce centre de masse.
La position de ce centre de masse est au centre de la balle soit d/2=20 mm.
On peut considérer la balle comme un point.
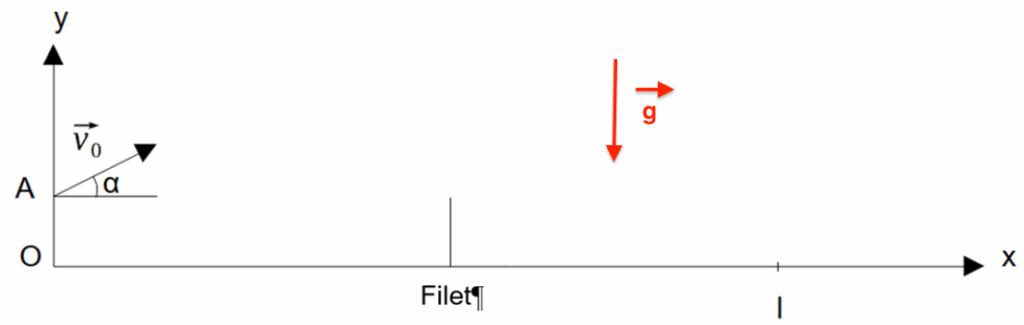
5. Indiquer, dans le cadre du modèle choisi, les caractéristiques (direction, sens et valeur) de la force appliquée à la balle pendant son mouvement.
La force appliquée à la balle pendant son mouvement est le poids $\vec{P}$ :
direction : verticale
sens : vers le bas
valeur : $P=mg=2{,}7.{10}^{-3}\times 9{,}8=2{,}7.{10}^{-2}\ \text{N}$
6. Montrer que les coordonnées cartésiennes du vecteur vitesse du centre de masse de la balle au cours de son mouvement sont données par les relations :
$\overrightarrow{v}= \begin{cases} v_x(t)=v_0 cos \alpha \\ v_y(t)=-gt+v_0 sin\alpha \end{cases}$
Réponse :
Système {balle }
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$\sum_{}^{}\overrightarrow{F}_{ext}=m\overrightarrow{a}$
$\overrightarrow{P}=m\overrightarrow{a}$
$m\overrightarrow{g}=m\overrightarrow{a}$
$\overrightarrow{a}=\overrightarrow{g}$
Or
$\overrightarrow{g} \begin{cases} 0 \\-g \end{cases}$
$\overrightarrow{a} \begin{cases} a_{x}(t)=0 \\a_{y}(t)=-g \end{cases}$
$\overrightarrow{a}=\frac{d \overrightarrow{v}}{dt}$
On intègre le système d’équation précédent :
$\overrightarrow{v} \begin{cases} v_{x}(t)=C_{1} \\v_{y}(t)=-gt+C_{2}\end{cases}$
Pour trouver les constantes, on utilise $\overrightarrow{v_0}$ :
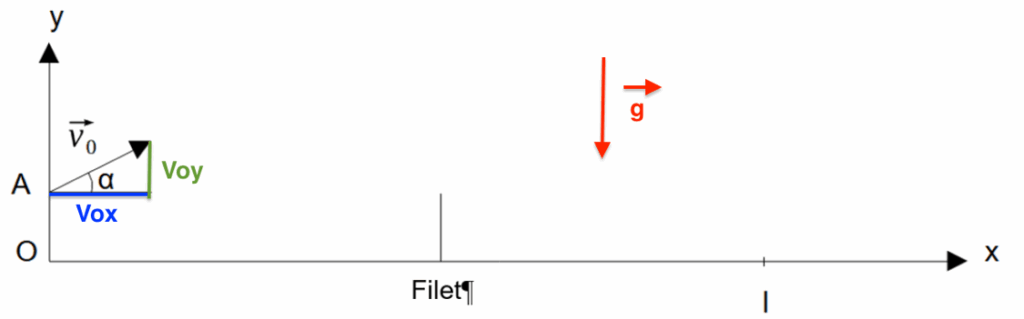
$\overrightarrow{v} \begin{cases} v_{0x}=v_{0}\cos\alpha \\v_{0y}=v_{0}\sin\alpha\end{cases}$
d’ou
$\overrightarrow{v} \begin{cases} v_{x}(t)=v_{0}\cos\alpha \\v_{y}(t)=-gt+v_{0}\sin\alpha\end{cases}$
7. Déterminer les équations horaires donnant les coordonnées x(t) et y(t) du centre de masse.
Réponse :
$\overrightarrow{v}=\frac{d \overrightarrow{OG}}{dt}$
On intègre le système d’équation précédent :
$\overrightarrow{OG} \begin{cases} x(t)=v_{0}\cos\alpha \times t +C_{3} \\y(t)=-\frac{1}{2}gt^2+v_{0}\sin\alpha\times t + C_{4}\end{cases}$
Pour trouver les constantes, on utilise $\overrightarrow{OM}_0$
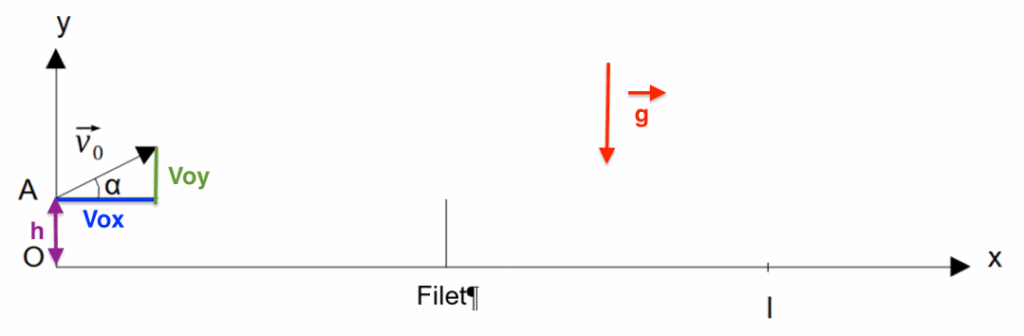
$\overrightarrow{OA} \begin{cases} x_A=0 \\y_A=h\end{cases}$
d’ou
$\overrightarrow{OG} \begin{cases} x(t)=v_{0}\cos\alpha \times t \\y(t)=-\frac{1}{2}gt^2+v_{0}\sin\alpha\times t + h\end{cases}$
8. L’impact de la balle sur la table a lieu à l’instant tI valant approximativement 0,55 s. Montrer que la balle tombe sur la table.
D’après l’énoncé : « À la date $t_I$, elle touche la table au point d’impact $I$ de coordonnées $(x_I;0)$. »
Calculons $x$ pour $t=0{,}55\ \text{s}$
$$x(t)=v_0\cos(\alpha), t$$
$$x(t)=5{,}0\cos(30)\times 0{,}55$$
$$x(t)=2{,}4\ \text{m}$$
$x(t)=2{,}4\ \text{m}$
Le point $O$ est au bord de la table et l’axe $Ox$ est parallèle au grand côté de la table dont la longueur est $2{,}74\ \text{m}$.
$x<2{,}74\ \text{m}$ : La balle tombe sur la table
9. Calculer la valeur de la tension U délivrée par un capteur situé au point d’impact.
Pour calculer $U$, calculons la vitesse $v_y$ :
$$v_{y(t)}=-gt+v_0\ \sin \alpha$$
$$v_{y(t=0{,}55)}=-9{,}8\times 0{,}55+5{,}0\sin(30)$$
$$v_{y(t=0{,}55)}=-2{,}9\ \text{m·s}^{-1}$$
$$|v_{y(t=0{,}55)}|=2{,}9\ \text{m·s}^{-1}$$
Or, la tension électrique $U$ est proportionnelle à $|v_y|$ pour des vitesses d’impact $|v_y|$ inférieures à $4{,}5\ \text{m·s}^{-1}$. (Question 1)
1ère méthode.
D’après la question 1 :
$$U=0{,}78 \times |v_y|$$
$$U=0{,}78 \times 2{,}9$$
$$U=2{,}3\ \text{V}$$
2nde méthode.
D’après le programme python :
$$v=1{,}3 \times U$$
$$1{,}3 \times U=v$$
$$U=\frac{v}{1{,}3}$$
$$U=\frac{2{,}9}{1{,}3}$$
$$U=2{,}2\ \text{V}$$
