Métropole Septembre 2022 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1ME3
Sujet et corrigé
Mots-clés : mouvement d’un satellite
La Station Spatiale Internationale (ISS) est un satellite artificiel de la Terre, observable de la surface de la Terre sous certaines conditions. C’est ainsi que, le 24 juin 2020, dans l’état de Virginie aux États-Unis, un astrophysicien a observé et enregistré le passage de l’ISS devant le Soleil. Pendant ce passage, la station spatiale se trouve entre le Soleil et le point d’observation. En réalisant une chronophotographie, on obtient l’image reproduite sur la figure 2.

Source : NASA
Le but de cet exercice est de déterminer la vitesse de l’ISS à l’aide d’une loi de la mécanique puis en exploitant la chronophotographie et de comparer les résultats obtenus.
Données :
- altitude moyenne de l’ISS : h = 419 km ;
- constante de gravitation universelle : G = 6,67×10–11 m3·kg–1·s–2 ;
- distance Terre-Soleil : dTS = 153×106 km ;
- diamètre du Soleil : D = 1,39×106 km ;
- masse de la Terre : MT = 5,97×1024 kg ;
- rayon de la Terre : RT = 6 371 km.
1. Détermination de la vitesse à l’aide d’une loi de la mécanique
La Station Spatiale Internationale est modélisée par un point matériel M, de masse m en orbite circulaire à la distance R du centre de la Terre, de masse MT. La Terre est supposée à répartition sphérique de masse, de centre T. Le mouvement de l’ISS est étudié dans le référentiel géocentrique d’origine prise au centre de la Terre et dont les axes pointent en direction d’étoiles lointaines ; il est supposé galiléen. On considère que seule l’interaction gravitationnelle avec la Terre est prise en compte.
Q1. Schématiser, sans souci d’échelle, la Terre et l’ISS. Placer le repère de Frenet $( \overrightarrow{U_N} $ , $ \overrightarrow{U_T} )$ et représenter la force à laquelle est soumise l’ISS.
Réponse :

Q2. Donner, dans ce repère, l’expression vectorielle de la force à laquelle est soumise l’ISS.
Réponse :
$\overrightarrow{F}_{T/ISS}=G\times \frac{M\times M_{T}}{R^2}\overrightarrow{u_n}$
Q3. Déduire de la seconde loi de Newton, l’expression suivante de la vitesse v de l’ISS :
$v= \sqrt{\frac{Gm_T}{R}} $
Réponse :
Système : ISS
Référentiel : Géocentrique supposé galiléen
D’après la 2nd loi de Newton :
$\sum_{}^{}\overrightarrow{F_{ext}}=M\overrightarrow{a}$
$\overrightarrow{F}_{T/ISS}=m\overrightarrow{a}$
$G\times \frac{M\times M_{T}}{R^2}\overrightarrow{u_n}=M\overrightarrow{a}$
$\overrightarrow{a}=G\times \frac{M_{T}}{R^2}\overrightarrow{u_n}$
Or, pour un mouvement circulaire, dans la base de Frenet, le vecteur accélération est de la forme :
$\vec{a}=\frac{v^2}{R}\vec{u_n}+\frac{dv}{dt}\vec{u_t}$
L’accélération étant unique, par identification :
$\frac{v^2}{R}=G\ \times \frac{M_T}{R^2}$
donc
$v=\sqrt{\frac{G\times M_{T}}{R}}$
Q4. Calculer la valeur de la vitesse v de l’ISS.
$$v=\sqrt{G\times\frac{M_T}{R}}$$
Avec $R=R_T+h$
$$v=\sqrt{G\times\frac{M_T}{R_T+h}}$$
$$v=\sqrt{6,67\times10^{-11}\times\frac{5,97\times10^{24}}{6371\times10^3+419\times10^3}}$$
$$v=7,66\times10^3\ m.s^{-1}$$
2. Estimation de la vitesse de l’ISS à partir d’une chronophotographie
Le télescope utilisé pour réaliser la chronophotographie lors du passage de l’ISS devant le Soleil est situé au point O. Les positions réelles successives de la station sont repérées par des points Mi, i allant de 0 à 5. Les points Si, i allant de 0 à 5, correspondent à la projection des points Mi sur le disque solaire, vus de la Terre (figure 2). La distance S0S5 observée permet de déterminer la distance parcourue par l’ISS notée M0M5.
La figure 1 représente, sans souci d’échelle, la situation. Les points M0 et M5 correspondent aux positions extrêmes de l’ISS pendant l’observation, ainsi que leur projection sur le disque solaire S0 et S5. La durée du mouvement entre deux positions successives (exemple de M0 à M1, de M1 à M2…) vaut Δt = 0,11 s.
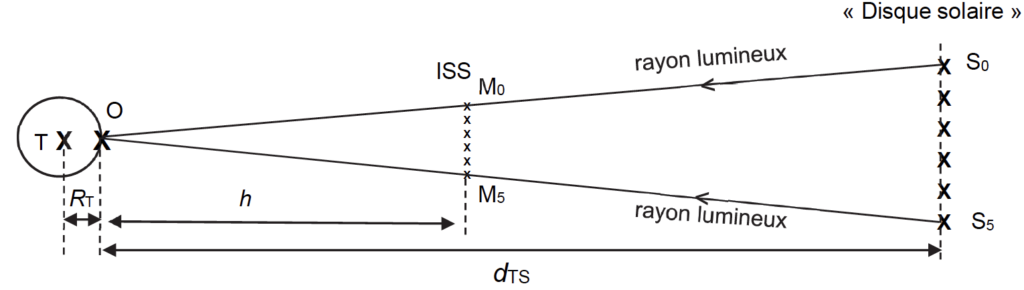
Figure 1. Schéma sans souci d’échelle de la situation
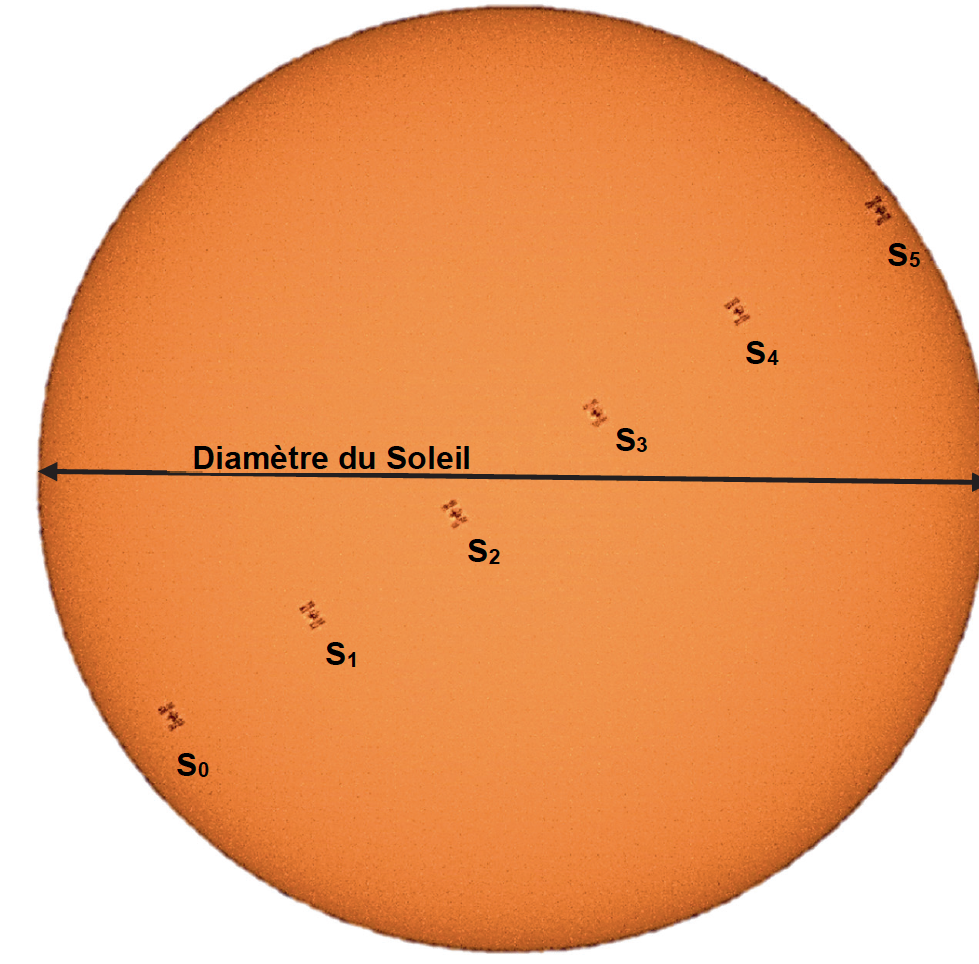
Figure 2. Chronophotographie de l’ISS lors de son passage devant le Soleil (Nasa, Joel Kowsky)
Dans cette partie, l’étude est réalisée dans le référentiel terrestre et les hypothèses formulées sont les suivantes :
- le mouvement de la station est rectiligne uniforme pendant la durée nécessaire à la réalisation de la chronophotographie ;
- les effets des mouvements de rotation de la Terre sur elle-même et de révolution de la Terre autour du Soleil ne sont pas pris en compte ;
- M0M5 et S0S5 sont considérés comme étant des droites.
Q5. En exploitant notamment la chronophotographie donnée en figure 2 et le schéma de la figure 1, estimer la valeur de la vitesse v de l’ISS dans le référentiel d’étude lors de l’observation. Commenter la valeur obtenue au regard de celle calculée à la question Q4. Donner au moins un argument qui justifie l’écart constaté.
Le candidat est invité à prendre des initiatives et à présenter sa démarche même si elle n’a pas abouti. La démarche suivie est évaluée et nécessite donc d’être correctement présentée.
| Schéma | Réel | |
| Diamètre du Soleil | 10,0 cm | $D=1,39\times10^6\ km$ |
| S0S5 | 9,20 cm | S0S5 |
$$S_0S_5=\frac{9,20\times1,39\times10^6}{10,0}$$
$$S_0S_5=1,28\times10^6\ km$$
D’après la figure 1 : considérons les triangles $OM_0M_5$ et $OS_0S_5$.
$M_0M_5$ et $S_0S_5$ sont parallèles. Nous pouvons utiliser le théorème de Thalès :
$$\frac{M_0M_5}{S_0S_5}=\frac{h}{d_{TS}}$$
$$M_0M_5=\frac{h}{d_{TS}}\times S_0S_5$$
$$M_0M_5=\frac{419\times10^3}{153\times10^6\times10^3}\times1,28\times10^6\times10^3$$
$$M_0M_5=3,5\times10^3\ m$$
Estimons la valeur de la vitesse $v$ de l’ISS dans le référentiel d’étude lors de l’observation :
$$v=\frac{d}{t}$$
$$v=\frac{M_0M_5}{5\times0,11}$$
$$v=\frac{3,5\times10^3}{5\times0,11}$$
$$v=6,4\times10^3\ m.s^{-1}$$
La valeur de la vitesse obtenue est inférieure à celle calculée à la question Q4 mais du même ordre de grandeur.
Cette vitesse est calculée en faisant notamment l’hypothèse que le mouvement de la station est rectiligne uniforme pendant la durée nécessaire à la réalisation de la chronophotographie.
Or le mouvement de la station n’est pas rectiligne uniforme, ce qui pourrait expliquer l’écart constaté.
