Vol d’une montgolfière

Bac Métropole Septembre 2021 Sujet 2

Exercice 1 – (10 points) –  Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée

Sujet n° 21-PYCJ2ME3

[latexpage]

Une montgolfière est un moyen de transport aérien constitué d’une nacelle pouvant contenir des passagers.

Au-dessus de la nacelle, se trouvent :

• une enveloppe en nylon appelée le ballon dont on considère le volume constant ;
• un brûleur permettant de réaliser la combustion de propane dans le dioxygène de l’air ; ce propane est stocké dans des bonbonnes transportées dans la nacelle.

De nombreuses sorties sont proposées, d’une durée moyenne d’une heure. Une voiture est contrainte de suivre au sol la montgolfière pour récupérer les passagers et le matériel lors de l’atterrissage. En effet, le lieu d’atterrissage ne peut pas être connu de façon sûre au moment du départ : il est dépendant des conditions météorologiques.

Les objectifs de cet exercice sont :

• de  déterminer  la  masse  totale  qu’il  est  possible  d’embarquer  dans  la montgolfière ;
• de trouver l’autonomie de vol maximale possible avec la montgolfière.

On étudie dans cet exercice une enveloppe en nylon de modèle « M-77 » de 0,1 mm d’épaisseur, de volume V = 2 200 m³, à laquelle on accroche une nacelle de modèle « C-1 », de masse m_nacelle = 56 kg. La nacelle est capable d’embarquer jusqu’à trois personnes ainsi que quatre bonbonnes pesant chacune 40 kg et contenant 20 kg de propane chacune.

D’après le site Internet https://escholarship.org/

Données :

• intensité de la pesanteur terrestre : g = 9,81 m·s^–2 ;
• surface de l’enveloppe du ballon : S = 847 m² ;
• masse par unité de surface de l’enveloppe en nylon : φ_nylon = 65 g·m^–2   ;
• constante du gaz parfait : R = 8,314 J·mol^–1·K^–1 ;
• masse molaire de l’air : M_air = 29,0 g·mol^–1.

1. Détermination de la masse totale qu’il est possible d’embarquer dans la montgolfière

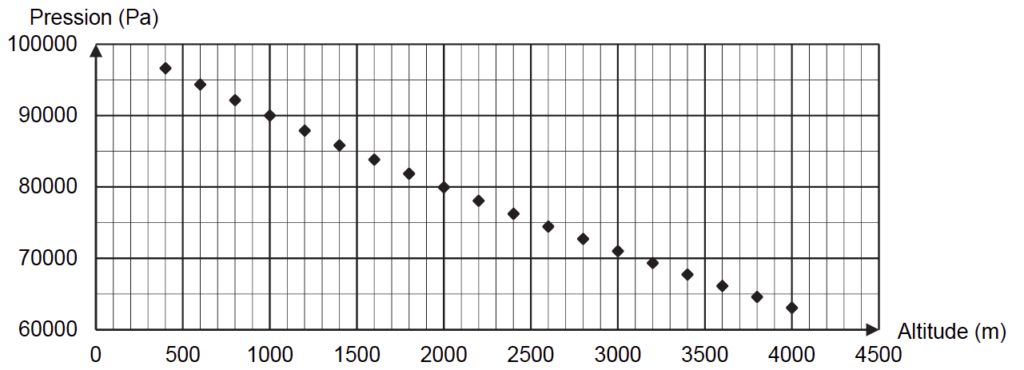
Au cours d’un vol, la montgolfière se trouve à une altitude de 1,5 km. On considère que la pression p à l’intérieur du ballon est égale à la pression à l’extérieur du ballon. La figure 1 présente l’évolution de la pression de l’air en fonction de l’altitude. L’air est considéré comme un gaz parfait.

Le brûleur n’est pas actionné au moment où on étudie le système.

1.1. Étude du système « ballon ».

1.1.1. À l’aide de l’équation d’état du gaz parfait, exprimer la masse volumique de l’air contenu dans le ballon ρ_int en fonction de la pression p, M_air, R et T, la température de l’air contenu dans le ballon.

$$\rho_{int}=\frac{m}{V}$$

Or

$$pV=nRT$$
$$V=\frac{nRT}{p}$$

$$\rho_{int}=m\times\frac{p}{nRT}$$

Or

$$n=\frac{m}{M}$$
$$m=n\times M$$
$$\rho_{int}=n\times M\times\frac{p}{nRT}$$
$$\rho_{int}=M\times\frac{p}{RT}$$

1.1.2. Montrer que la valeur de la masse volumique de l’air contenu dans le ballon ρ_int lorsque le ballon est à une altitude de 1,5 km est de l’ordre de 0,8 kg·m^–3. On suppose que la température de l’air à l’intérieur du ballon à l’instant où on étudie le système est à 373 K.

1.2. Étude du système « montgolfière ».

On suit le déplacement du centre de masse G de la montgolfière. On se place dans le référentiel terrestre supposé galiléen muni d’un repère d’espace (O,$\overrightarrow{i}$,$\overrightarrow{k}$) présenté sur la figure 2. L’origine au point O est au niveau du sol, au point de décollage de la montgolfière.

On considère qu’il s’exerce seulement deux forces sur le système {montgolfière} composé de la nacelle, de son chargement et du ballon :

• le poids $\overrightarrow{P}$ ;
• la poussée d’Archimède  qui  modélise  l’action  de  l’air  sur  le  ballon : $\overrightarrow{P_A}$ = ρ_ext × V × g × $\overrightarrow{k}$où ρ_ext représente la masse volumique de l’air extérieur et V représente le volume total de la montgolfière, dont on considère qu’il est égal au volume du ballon.

On considère que la masse d’air présente dans le ballon est constante et que la montgolfière, de masse totale m, reste immobile. À la température locale et à l’altitude du vol de 1,5 km, la masse volumique de l’air extérieur au ballon vaut 1,06 kg·m^–3 tandis que la masse volumique de l’air à l’intérieur du ballon vaut 0,80 kg·m^–3.

1.2.1. Représenter les deux forces s’exerçant sur la montgolfière dans le cas où elle est immobile dans le référentiel terrestre, sans souci d’échelle en utilisant le système d’axes de la figure 2. Justifier.

Le poids est vertical et dirigé vers le bas.

La poussée d’Archimède est verticale et dirigée vers le haut.

Lorsque la montgolfière est immobile, les forces se compensent : la norme du poids et de la poussé d’Archimède est identique.

1.2.2. Donner l’expression vectorielle du poids $\overrightarrow{P}$ de la montgolfière.

$$\vec{P}=m\vec{g}$$

1.2.3. Établir l’expression vectorielle de la poussée d’Archimède $\overrightarrow{P_A}$ en fonction de g, m et $\overrightarrow{k}$.

Lorsque la montgolfière est immobile : d’après la 1^ère loi de Newton :

$$\Sigma{\vec{F}}_{ext}=\vec{0}$$
$$\vec{P}+\vec{P_A}=\vec{0}$$
$$\vec{P_A}=-\vec{P}$$
$$\vec{P_A}=-m\vec{g}$$
$$\vec{P_A}=mg\vec{k}$$

1.2.4. En déduire la masse totale embarquée dans la nacelle à cette altitude. Commenter.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

$$\vec{P_A}=mg\vec{k}$$

Or

$$\vec{P_A}=\rho_{ext}\times V\times g\times\vec{k}$$

D’où

$$\rho_{ext}\times V\times g\times\vec{k}=mg\vec{k}$$
$$\rho_{ext}\times V\times g=mg$$
$$\rho_{ext}\times V=m$$
$$m=\rho_{ext}\times V$$
$$m=1,06\times2200$$
$$m=2,32.{10}^3\ Kg$$

Comparons avec la masse totale de la montgolfière :

$$m_T=m_{envellope}+m_{air}+m_{nacelle}+m_{personnes}+m_{bonbonnes}$$

$$m_{air}=\rho_{air}\times V$$
$$m_{air}=0,8\times2200=1,7.{10}^3\ Kg$$

$$m_{envellope}=\varphi_{nylon}\times S$$
$$m_{envellope}=65.{10}^{-3}\times847=55\ Kg$$

$$m_{bonbonnes}=4\times(m_{bonbonne}+m_{propane})$$
$$m_{bonbonnes}=4\times(40+20)=2,4.{10}^2\ Kg$$

On fait l’hypothèse qu’une personne pèse 70 Kg

$$m_{personnes}=3\times70=2,1.{10}^2\ Kg$$

$$m_T=m_{envellope}+m_{air}+m_{nacelle}+m_{personnes}+m_{bonbonnes}$$
$$m_T=55+1,7.{10}^3+56+2,1.{10}^2+2,4.{10}^2$$
$$m_T=2,3.{10}^3\ Kg$$

Les deux masses correspondent.

2. Détermination de l’autonomie maximale de vol de la montgolfière

En réalité, la montgolfière ne reste pas à une altitude constante. Son altitude varie autour d’une altitude moyenne, au gré de l’actionnement du brûleur par le pilote. L’utilisation du brûleur est nécessaire pour maintenir une altitude moyenne constante.

On considère que la montgolfière est en vol, stabilisée à une altitude moyenne de 1,5 km. La température extérieure est T_ext = 278 K au cours d’un vol.

On cherche à établir le bilan énergétique entre le système {air à l’intérieur de l’enveloppe + enveloppe} et le milieu extérieur.

2.1. Nommer les trois modes de transferts thermiques. Caractériser qualitativement ces trois modes.

Un transfert thermique peut avoir lieu par :

• Conduction : il y a contact entre les corps de température différente. L’énergie se transmet de proche en proche.
• Convection : il y a transfert de matière. L’énergie est transportée par les déplacements du fluide
• Rayonnement : l’absorption ou l’émission d’un rayonnement.

La figure 3 présente les transferts thermiques qui ont lieu entre le système {ballon} et le milieu extérieur. On rappelle que le ballon représente l’enveloppe en nylon et l’air contenu à l’intérieur. En régime stationnaire, la montgolfière est en équilibre thermique.

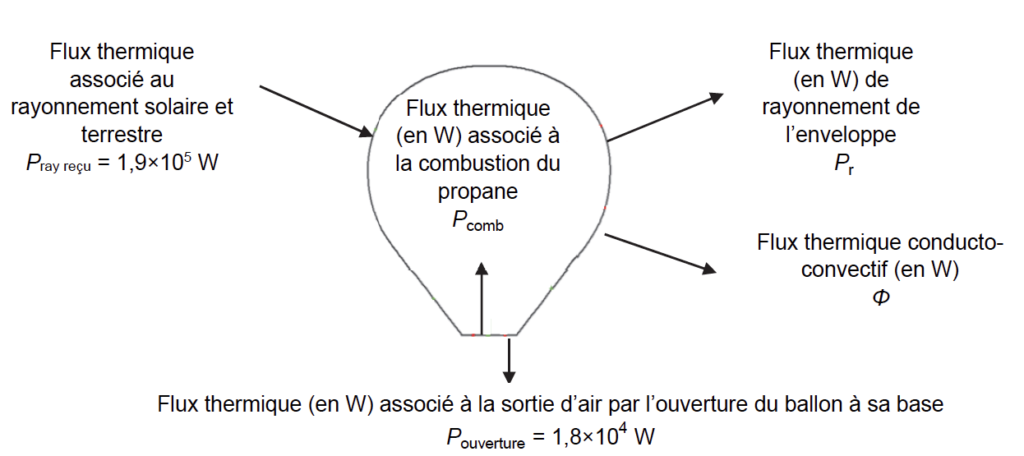
2.2. À l’aide de la figure 3, établir une relation littérale entre les flux thermiques impliqués pour le système lorsque la montgolfière est à l’équilibre thermique.

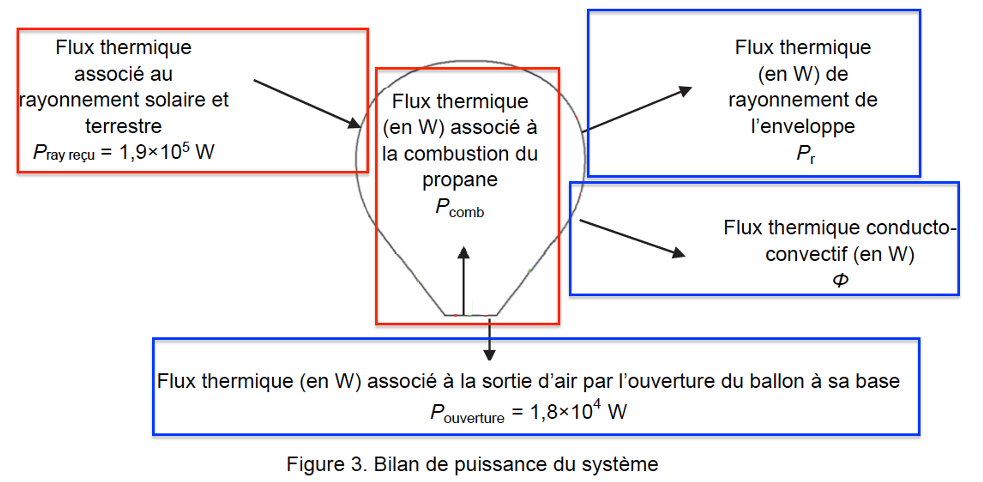
$$P_{ray\ recu}+P_{comb}+P_{ouverture}+P_r+\Phi=0$$

Remarque : les puissances reçues sont comptées positivement, les puissances données sont comptées négativement.

Une partie du transfert thermique a lieu sous forme de rayonnement de l’enveloppe vers le milieu extérieur. Le calcul du flux thermique rayonné se fait grâce à la relation de Stefan-Boltzmann : P_r = ε· σ·S·T⁴ avec :

• P_r le flux thermique rayonné ;
• ε le coefficient d’émissivité constant sans unité, pour l’enveloppe du ballon : ε = 0,87 ;
• σ la constante de Stefan : σ = 5,67 × 10^–8 W·m^–2·K^–4;
• S la surface de l’enveloppe ;
• T la température de surface de l’enveloppe en K.

De plus, les mouvements de l’air extérieur le long de l’enveloppe sont à l’origine d’un flux thermique transféré vers  l’extérieur  par  un  phénomène  de  conducto-convection  que  l’on  peut  calculer  grâce  à la relation suivante : $\phi=\frac{\Delta T}{R_{th}}$

• Φ représente le flux thermique perdu par le système par conducto-convection en W ;
• ∆T représente la différence de température entre l’enveloppe et le milieu extérieur en K ;
• R_th  représente la résistance thermique associée au flux thermique entre l’enveloppe et le milieu extérieur : R_th = 3,5×10^–4 K·W^–1.

D’après l’étude, dans ces conditions, la température de l’enveloppe vaut T = 325 K, température intermédiaire entre celle de l’air à l’intérieur du ballon et celle de l’air à l’extérieur du ballon.

2.3. Calculer le flux thermique par rayonnement P_r émis par l’enveloppe vers le milieu extérieur.

$$P_r=-\varepsilon\times\sigma\times S\times T^4$$
$$P_r=-0,87\times5,67.{10}^{-8}\times847\times{(325)}^4$$
$$P_r=-4,66.{10}^5\ W$$

2.4. Calculer le flux conducto-convectif Φ.

$$\Phi=\frac{\Delta T}{R_{th}}$$
$$\Phi=\frac{278-325}{3,5.{10}^{-4}}$$
$$\Phi=-1,34.{10}^5\ W$$

2.5. En déduire que la valeur du flux thermique P_comb  associé à la combustion du propane en régime de croisière est de l’ordre de 4×10⁵ W.

$$P_{ouverture}+P_r+\Phi+P_{ray\ recu}+P_{comb}=0$$
$$P_{comb}=-P_{ouverture}-P_r-\Phi-P_{ray\ recu}$$
$$P_{comb}=-(-1,8.{10}^4)-(-4,66.{10}^5)-(-1,34.{10}^5)-1,9.{10}^5$$
$$P_{comb}=4,28.{10}^5\ W$$

Le flux thermique associé à la combustion du propane n’est pas libéré de façon continue. En effet, la combustion du propane n’a lieu que lorsque le brûleur fonctionne. L’énergie de combustion massique du propane est : E_comb = 46,4 MJ·kg^–1.

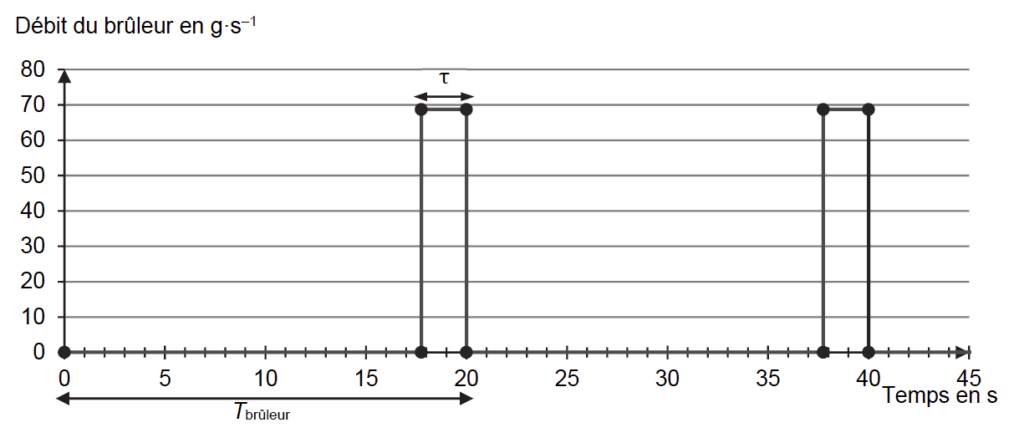
Le pilote actionne le brûleur pendant une durée r selon le fonctionnement décrit sur la figure 4.

Lorsque le brûleur est en fonctionnement, 68 grammes de propane sont brûlés chaque seconde.

2.6. Montrer que le flux thermique associé à la combustion du propane lorsque le brûleur est en fonctionnement est de l’ordre de 3×10⁶ W.

$$P=\frac{E}{\Delta t}$$

Or

$$E=m\times E_{comb}$$
$$P=\frac{m\times E_{comb}}{\Delta t}$$

Avec :

$$\Delta t=\tau=2\ s$$
$$m=2\times68\ g=136\ g$$

$$P=\frac{2\times68.{10}^{-3}\times46,4.{10}^6}{2}$$
$$P=3,2.{10}^6\ W$$

2.7. Dans les conditions de l’étude, déterminer la durée maximale de vol qu’il est possible de réaliser à l’aide du propane embarqué dans la montgolfière. Commenter.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.

Calculons $E_{total}$ disponible dans les 4 bonbonnes contenant 20 kg de propane chacune, soit 80 kg de propane.

$$E_{total}=m\times E_{comb}$$
$$E_{total}=80\times46,4.{10}^6$$
$$E_{total}=3,7.{10}^9\ J$$

Pour une durée $\tau=2\ s$ de combustion, $T_{brûleur}=20\ s$

$$E=m\times E_{comb}$$
$$E=2\times68.{10}^{-3}\times46,4.{10}^6$$
$$E=6,3.{10}^6\ J$$

Trouvons la durée de fonctionnement :

$E=6,3.{10}^6\ J$	Tbrûleur=20 s
$E_{total}=3,7.{10}^9\ J$	t

$$t=\frac{3,7.{10}^9\times20}{6,3.{10}^6}$$
$$t=1,2.{10}^4\ s$$
$$t=3h\ 20\ min$$

Ce temps semble cohérent pour un vol de montgolfière.