Bac Métropole Septembre 2024 Sujet 2
Exercice 1 – (11 points) – Durée 1h56 – Calculatrice autorisée
Sujet n°24-PYCJ2ME3
Sujet et corrigé
Exercice 1 – Vol en montgolfière (11 points)
Inventée à la fin du XVIIIe siècle par les frères Montgolfier, la montgolfière est la première machine ayant permis à l’Homme de voler.
L’objectif de cet exercice est d’étudier l’envol d’une montgolfière ainsi que les transferts thermiques à travers son enveloppe.

D’après le site France Bleu Pyrénées-Orientales
1. L’envol de la montgolfière
Une montgolfière se compose de trois parties principales : une enveloppe dont le volume est considéré constant, un système de chauffage (brûleur avec réservoir de carburant) et une nacelle.
On étudie dans cette partie l’envol de la montgolfière dans le référentiel terrestre supposé galiléen. Dans cette modélisation, les seules forces prises en compte sont le poids de la montgolfière et la poussée d’Archimède exercée par l’air ambiant sur celle-ci.
Données :
- masses molaires atomiques : M(O) = 16×10-3 kg·mol–1, M(N) = 14×10-3 kg·mol–1 ;
- intensité de la pesanteur terrestre supposée constante : g = 9,81 m·s–2 :
- l’air, assimilé à un gaz parfait, est composé, en quantité de matière, de 80 % de diazote N2 et de 20 % de dioxygène O2 ;
- constante des gaz parfaits : R = 8,31 J·mol–1·K–1;
- conversion d’une température θ exprimée en degré Celsius en une température T en Kelvin : T(K) = θ(°C) + 273 °C ;
- la poussée d’Archimède $\overrightarrow{\pi}_A$ est unune force, verticale et dirigée vers le haut, que subit tout objet plongé dans un fluide. Pour un objet de volume V totalement immergé dans un fluide de masse volumique ρ, la valeur πA de la poussée d’Archimède a pour expression :
πA = ρ∙V∙g
- caractéristiques de l’air extérieur au niveau du sol :
- masse volumique : ρext = 1,2 kg·m–3 ;
- température : θext = 21 °C ;
- pression atmosphérique : patm = 1,0×105 Pa ;
- la montgolfière étudiée est constituée d’une enveloppe de volume V invariable égal à 2,5×103 m3 et d’une nacelle de volume négligeable par rapport à celui de l’enveloppe ;
- la masse mens de l’ensemble comprenant la nacelle, l’enveloppe, le système de chauffage et les passagers est égale à 500 kg.
Q1. Montrer que la valeur de la masse molaire Mair de l’air est voisine de 29×10–3 kg·mol–1.
D’après les données : « l’air, assimilé à un gaz parfait, est composé, en quantité de matière, de 80 % de diazote N2 et de 20 %de dioxygène O2 ; »
$M_{air}=\frac{80}{100}\times M_{N_2}+\frac{20}{100}\times M_{O_2}$
$M_{air}=\frac{80}{100}\times 2\times M_N+\frac{20}{100}\times 2\times M_O$
$M_{air}=\frac{80}{100}\times 2\times 14\times {10}^{-3}+\frac{20}{100}\times 2\times 16\times {10}^{-3}$
$M_{air}=2,9\times {10}^{-2}\ Kg\cdot {\rm mol}^{-1}$
$M_{air}=29\times {10}^{-3}\ Kg\cdot {\rm mol}^{-1}$
Ainsi, la valeur de la masse molaire Mair de l’air est voisine de 29×10–3 kg·mol–1.
Q2. En exploitant l’équation d’état des gaz parfaits, exprimer littéralement la masse mint de l’air contenu à l’intérieur de l’enveloppe en fonction de la pression pint de l’air à l’intérieur, du volume V de l’enveloppe, de la masse molaire Mair de l’air, de la constante R des gaz parfaits et de la température Tint de l’air situé à l’intérieur de l’enveloppe.
$p_{int}\times V=n_{int}\times R\times T_{int}$
Or
$n_{int}=\frac{m_{int}}{M_{air}}$
D’ou
$p_{int}\times V=\frac{m_{int}}{M_{air}}\times R\times T_{int}$
$\frac{m_{int}}{M_{air}}\times R\times T_{int}=p_{int}\times V$
$m_{int}=\frac{p_{int}\times V\times M_{air}}{R\times T_{int}}$
Q3. Exprimer le poids total du système {montgolfière + air intérieur}, noté Ptotal, en fonction des masses mens et mint.
Poids total du système {montgolfière + air intérieur} :
$P_{total}=m_{total}\times g$
Or
$m_{total}=m_{int}+m_{ens}$
D’ou
$P_{total}=\left(m_{int}+m_{ens}\right)\times g$
Q4. Calculer la valeur de la poussée d’Archimède πA qui s’exerce sur le système {montgolfière + air intérieur}, au niveau du sol.
$\pi_A=\rho_{ext}\times V\times g$
$\pi_A=1,2\times 2,5\times {10}^3\times 9,81$
$\pi_A=2,9\times {10}^4\ N$
Q5. Montrer que l’expression de la valeur de la température minimale Tmin de l’air à l’intérieur de l’enveloppe pour que la montgolfière puisse décoller est :
$$ T_{\min}=\frac{p_{int}\times V\times M_{air}}{R\times\left(\frac{\pi A}{g}-m_{ens}\right)} $$
Calculer la valeur de Tmin. On admet que la pression pint de l’air à l’intérieur de l’enveloppe est égale à la pression atmosphérique patm = 1,0×105 Pa.
Pour que la montgolfière puisse décoller il faut que la poussée d’Archimède soit supérieure au poids :
$\pi_A\geq P$
Or (D’après la question Q3.)
$P=\left(m_{int}+m_{ens}\right)\times g$
D’ou
$\pi_A\geq \left(m_{int}+m_{ens}\right)\times g$
Or (D’après la question Q2.)
$m_{int}=\frac{p_{int}\times V\times M_{air}}{R\times T_{int}}$
D’ou
$\pi_A\geq \left(\frac{p_{int}\times V\times M_{air}}{R\times T_{int}}+m_{ens}\right)\times g$
$\frac{\pi_A}{g}\geq \left(\frac{p_{int}\times V\times M_{air}}{R\times T_{int}}+m_{ens}\right)$
$\frac{\pi_A}{g}-m_{ens}\geq \frac{p_{int}\times V\times M_{air}}{R\times T_{int}}$
$\left(\frac{\pi_A}{g}-m_{ens}\right)\times T_{int}\geq \frac{p_{int}\times V\times M_{air}}{R}$
$T_{int}\geq \frac{p_{int}\times V\times M_{air}}{R\times \left(\frac{\pi_A}{g}-m_{ens}\right)}$
Ainsi, la valeur de la température minimale Tmin de l’air à l’intérieur de l’enveloppe pour que la montgolfière puisse décoller est :
$T_{min}=\frac{p_{int}\times V\times M_{air}}{R\times \left(\frac{\pi_A}{g}-m_{ens}\right)}$
$T_{min}=\frac{1,0\times {10}^5\times 2,5\times {10}^3\times 29\times {10}^{-3}}{8,31\times \left(\frac{2,9\times {10}^4}{9,81}-500\right)}$
$T_{min}=355\ K$
$T_{min}=355-273$
$T_{min}=82\ °C$
Alors que la montgolfière est retenue au sol par des sangles, le pilote actionne les brûleurs afin que la température de l’air intérieur de l’enveloppe soit supérieure à la température Tmin.
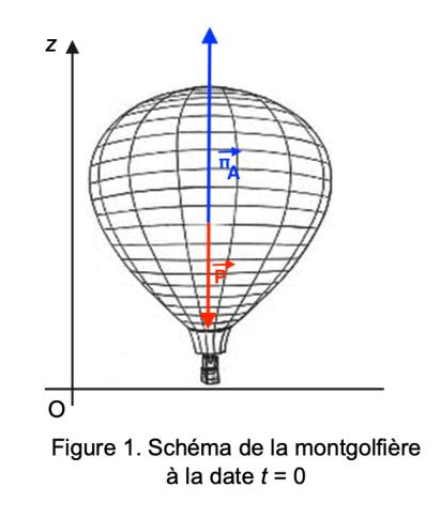
À la date t = 0, les sangles sont détachées et la montgolfière, initialement immobile, commence son ascension verticale, comme représenté à la figure 1. À cet instant, la valeur de la poussée d’Archimède exercée sur le système est égale à πA = 2,9×104 N et la masse totale du système {montgolfière + air intérieur} est mtot = 2,8×103 kg.
Figure 1. Schéma de la montgolfière à la date t = 0
Dans une modélisation simplifiée, on ne tient compte que de la poussée d’Archimède et du poids pour étudier le mouvement du ballon. On suppose également que les valeurs de ces forces restent inchangées au cours du temps.
Q6. Déterminer la valeur de l’accélération du système {montgolfière + air intérieur}. Calculer ensuite la valeur de sa vitesse au bout de 10 s puis au bout de 1 minute d’ascension.
Système {montgolfière + air intérieur}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$\Sigma \overrightarrow{F_{ext}}=m\overrightarrow{a}$
$\overrightarrow{P}+\overrightarrow{\pi_A}=m\overrightarrow{a}$
$m\overrightarrow{a}=\overrightarrow{P}+\overrightarrow{\pi_A}$
$\overrightarrow{a}=\frac{\overrightarrow{P}+\overrightarrow{\pi_A}}{m}$
Projetons sur l’axe z :
$a_z=\frac{-P+\pi_A}{m}$
$a_z=\frac{-m\times g+\pi_A}{m}$
$a_z=\frac{-2,8\times {10}^3\times 9,81+2,9\times {10}^4\ }{2,8\times {10}^3}$
$a_z=0,55\ m\cdot s^{-2}$
$a=\sqrt{{a_z}^2}$
$a=\sqrt{{0,55\ }^2}$
$a=0,55\ m\cdot s^{-2}$
$a_z=\frac{dv_{z\left(t\right)}}{dt}$
On intègre l’accélération :
$v_{z\left(t\right)}=0,55\times t+C_1$
Pour trouver les constantes, on utilise la vitesse initiale. Or, d’après le sujet, un dispositif permet de lâcher sans vitesse initiale et simultanément la boule de bowling et la plume : $v_{0z}=0$
d’ou
$v_{z\left(t\right)}=0,55\times t$
Calculons la valeur de sa vitesse au bout de 10 s puis au bout de 1 minute d’ascension :
$v_{z\left(t=10s\right)}=0,55\times 10$
$v_{z\left(t=10s\right)}=5,5\ m\cdot s^{-1}$
$v_{z\left(t=1\ min\right)}=0,55\times 1\times 60$
$v_{z\left(t=1\ min\right)}=33\ m\cdot s^{-1}$
Q7. Commenter les résultats obtenus à la question précédente et proposer une piste d’amélioration du modèle. On pourra s’appuyer sur les vitesses exprimées en km·h-1.
$v_{z\left(t=10s\right)}=5,5\ m\cdot s^{-1}=5,5\times 3,6=20\ km\cdot h^{-1}$
$v_{z\left(t=1\ min\right)}=33\ m\cdot s^{-1}=33\times 3,6\ =119\ km\cdot h^{-1}$
Les vitesses trouvées sont bien trop importantes pour une montgolfière.
Le modèle ne prend en compte que de la poussée d’Archimède et du poids pour étudier le mouvement du ballon. Il faut prendre en compte les forces de frottements.
2. Une enveloppe de montgolfière plus performante
Des entreprises spécialisées dans la conception des montgolfières ont développé une nouvelle gamme d’enveloppes. Contrairement aux enveloppes traditionnelles, constituées d’une simple couche de nylon, les nouveaux modèles d’enveloppes sont constitués d’une double couche de nylon. Entre les deux épaisseurs de nylon, une couche d’air permet de limiter le transfert thermique vers l’extérieur de l’enveloppe. La consommation de carburant est ainsi réduite.
Données :
- résistance thermique d’une enveloppe simple couche : Rth,1 = 3,0×10–4 K·W–1 ;
- on rappelle que le flux thermique $ \phi_1$ à travers l’enveloppe simple couche du ballon, de l’intérieur vers l’extérieur, est donné par la relation :
$$ \phi_1=\frac{\theta_{int}-\theta_{ext}}{R_{th,1}}$$
où θext = 21 °C est la température de l’air extérieur et où θint = 106 °C est la température de l’air intérieur.
Q8. Préciser, en justifiant, le sens du flux thermique à travers l’enveloppe simple couche du ballon.
Un transfert thermique se fait du corps chaud vers le corps froid.
$\theta_{int}=106\ °C$ est supérieure à $\theta_{ext}=21\ °C$ : le sens du flux thermique à travers l’enveloppe simple couche du ballon se fait de l’intérieure vers l’extérieur.
Q9. Calculer la valeur du flux thermique $ \phi_1$ à travers une enveloppe simple couche.
$\Phi_1=\frac{\theta_{int}-\theta_{ext}}{R_{th,1}}$
$\Phi_1=\frac{106-21}{3,0\times {10}^{-4}}$
$\Phi_1=2,8\times {10}^5\ W$
Q10. Le flux thermique $ \phi_2$ à travers l’enveloppe à double paroi est $ \phi_2$ = 165 kW. Commenter.
$\frac{\Phi_1}{\Phi_2}=\frac{2,8\times {10}^5}{165\times {10}^3}$
$\frac{\Phi_1}{\Phi_2}=1,7$
Le flux thermique φ1 à travers une enveloppe simple couche est 1,7 fois plus grand que le flux thermique φ2 à travers l’enveloppe à double paroi.
Le transfert thermique à travers l’enveloppe à double paroi est limité. La consommation de carburant est ainsi réduite.
3. Une gourde en aluminium à bord de la montgolfière
Le pilote de la montgolfière emporte avec lui une gourde en aluminium contenant une boisson chaude. On étudie en laboratoire l’évolution temporelle de la température du système {gourde + boisson} et on modélise le transfert thermique entre ce système et l’extérieur par la loi de Newton, rappelée dans les données ci- dessous.
La température du système à la date t est notée θ(t). À la date t = 0 correspondant au début de l’expérience, la température du système est θ0 = 48 °C.
Données :
- capacité thermique du système étudié : C = 2,1×103 J·K–1 ;
- surface totale de la gourde exposée à l’air : S = 0,042 m2 ;
- la température de l’air extérieur est supposée constante pendant toute la durée de l’expérience et égale à θext = 21 °C ;
- la loi de Newton donne l’expression du flux thermique ϕ (en W) reçu par le système {gourde + boisson}, à la température θ(t), de la part de l’air extérieur, à la température θext :
ϕ = h·S·(θext – θ(t)) où h est le coefficient d’échange thermique surfacique.
Lors de l’expérience réalisée en laboratoire, l’utilisation d’un système d’acquisition informatisé permet d’obtenir l’évolution de la température du système au cours du temps (figure 2).
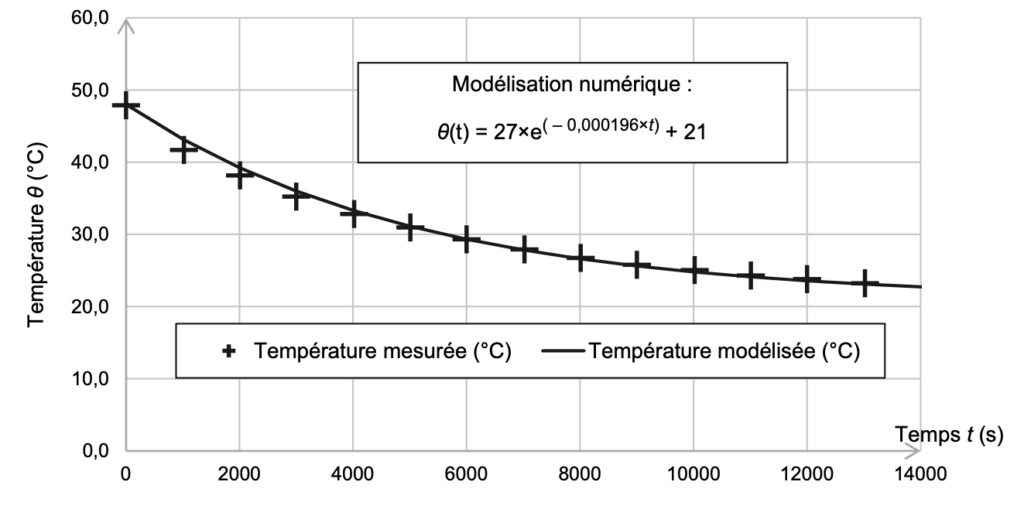
Figure 2. Courbe représentant l’évolution de la température θ du système au cours du temps
On considère deux instants voisins t et t + Δt, la durée Δt est supposée faible devant une durée caractéristique d’évolution de la température du système.
Q11. Montrer que la température du système vérifie la relation :
$$ \theta(t+\Delta t)-\theta(t)=\frac{h\times S\times\left(\theta_{ext}-\theta(t)\right)\times\Delta t}{C} $$
$\phi=\Delta U\Delta t$
$\Delta U\Delta t=\phi$
Or $\phi=h\cdot S\cdot \left(\theta_{ext}-\theta\left(t\right)\right)$
$\Delta U\Delta t=h\cdot S\cdot \theta_{ext}-\theta t$
Or
$\Delta U=C\times \Delta \theta$
$\Delta U=C\times \theta t+\Delta t-\theta t$
$C\times \theta t+\Delta t-\theta t\Delta t=h\cdot S\cdot \theta_{ext}-\theta t$
Ainsi, la température du système vérifie la relation :
$\theta t+\Delta t-\theta t=\frac{h\cdot S\cdot \theta_{ext}-\theta t\cdot \Delta t}{C}$
À partir du résultat précédent, on montre que la température θ(t) du système lors de son refroidissement vérifie l’équation différentielle suivante :
$$ \frac{d\theta(t)}{dt}+\frac{\theta(t)}{\tau}=\frac{\theta_{ext}}{\tau} $$
avec $\tau=\frac{C}{h\times S}$ le temps caractéristique du système.
L’équation différentielle précédente admet des solutions générales de la forme $\theta(t)=A\cdot e^{-\frac{t}{\tau}}+B$.
Q12. Déterminer les expressions littérales des constantes A et B en fonction de θ0 et θext puis calculer leurs valeurs. Commenter.
$\theta\left(t\right)=Ae^{-\frac{t}{\tau}}+B$
Si on attend suffisamment longtemps (lorsque le temps tend vers l’infini), la température tend vers la valeur de la température extérieure ($\theta\left(t\rightarrow\infty\right)=\theta_{ext}$) :
$\theta\left(t\rightarrow\infty\right)=Ae^{-\frac{\infty}{\tau}}+B$
$\theta\left(t\rightarrow\infty\right)=A\times 0+B$
$\theta\left(t\rightarrow\infty\right)=B$
Or
$\theta\left(t\rightarrow\infty\right)=\theta_{ext}$
Ainsi
$B=\theta_{ext}$
$B=21°C$
Initialement (lorsque le temps est nul), la température à pour la valeur de la température initiale ($\theta\left(t=0\right)=\theta_0$) :
$\theta\left(t=0\right)=Ae^{-\frac{0}{\tau}}+B$
$\theta\left(t=0\right)=A\times 1+B$
$\theta\left(t=0\right)=A+B$
Or
$\theta\left(t=0\right)=\theta_0$
D’ou
$A+B=\theta_0$
$A=\theta_0-B$
Or $B=\theta_{ext}$
Ainsi
$A=\theta_0-\theta_{ext}$
$A=48-21$
$A=27\ °C$
Ainsi :
$\theta\left(t\right)=27e^{-\frac{t}{\tau}}+21$
C’est en accord avec la Modélisation numérique :
$\theta\left(t\right)=27\times e^{\left(-0,000196\times t\right)}+21$
Q13. Déterminer la valeur du temps caractéristique 𝜏 à partir de la modélisation numérique de la figure 2.
$\theta\left(t\right)=27\times e^{-\frac{t}{\tau}}+21$
et
$\theta\left(t\right)=27\times e^{\left(-0,000196\times t\right)}+21$
Par identification :
$-\frac{t}{\tau}=-0,000196\times t$
$\frac{t}{\tau}=0,000196\times t$
$\frac{1}{\tau}=0,000196$
$1=0,000196\times \tau$
$0,000196\times \tau=1$
$\tau=\frac{1}{0,000196}$
$\tau=5,1\times {10}^3\ s$
Q14. En déduire la valeur du coefficient h d’échange thermique surfacique, puis commenter le résultat obtenu avec les valeurs données dans le tableau ci-dessous.
| Conditions environnementales | Coefficient d’échange thermique surfacique entre l’air et une paroi solide en W∙K−1∙m−2. |
| Sans courant d’air | de 5 à 10 |
| Avec courant d’air | de 10 à 500 |
D’après le cours de P.-Y. Lagrée, Coefficient d’échange, Ailettes
$\tau=\frac{C}{h\cdot S}$
$\tau\times h=\frac{C}{S}$
$h=\frac{C}{\tau\times S}$
$h=\frac{2,1\times {10}^3}{5,1\times {10}^3\times 0,042}$
$h=9,8\ W\cdot K^{-1}\cdot m^{-2}$
5 W∙K−1∙m−2 < h < 10 W∙K−1∙m−2 : les valeurs données dans le tableau nous indique que le coefficient d’échange thermique surfacique correspond à des conditions environnementales sans courant d’air.

