Bac Asie 2021 Sujet 2
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ2JA1
Mots-clés : mouvement dans un champ de pesanteur uniforme, lois de Newton, langage Python.
Le « water bottle flip » est un jeu d’adresse consistant à lancer une bouteille plastique partiellement remplie d’eau afin qu’elle se pose verticalement sur sa base sur une table placée à proximité. Il faut beaucoup s’entraîner pour réussir un « water bottle flip ». Initialement, la bouteille n’est tenue que par son col. Le mouvement ascendant du bras communique la vitesse juste suffisante à la bouteille. Tandis qu’elle monte puis redescend, celle-ci tourne sur elle-même.

Dans cet exercice, on se propose d’étudier le mouvement du centre de masse de la bouteille.
Le système considéré est l’ensemble {bouteille + eau} de masse m = 162 g dont on étudie le mouvement du centre de masse, noté G.
Le système évolue dans le champ de pesanteur terrestre ![]() uniforme.
uniforme.
On fait l’hypothèse que l’action de l’air est négligeable.
Le mouvement est étudié dans le système d’axes (Oxy) (Cf. figure 1).
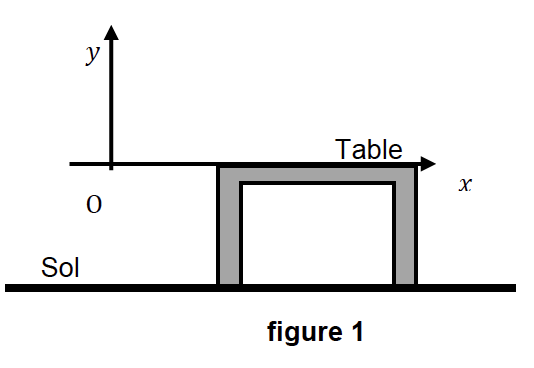
À la date 𝑡 = 0 s, le centre de masse G est placé à l’origine du repère O et sa vitesse initiale, notée ![]() , a une direction faisant un angle 𝛼 avec l’axe horizontal (Ox).
, a une direction faisant un angle 𝛼 avec l’axe horizontal (Ox).
Recherche des conditions initiales sur la vitesse
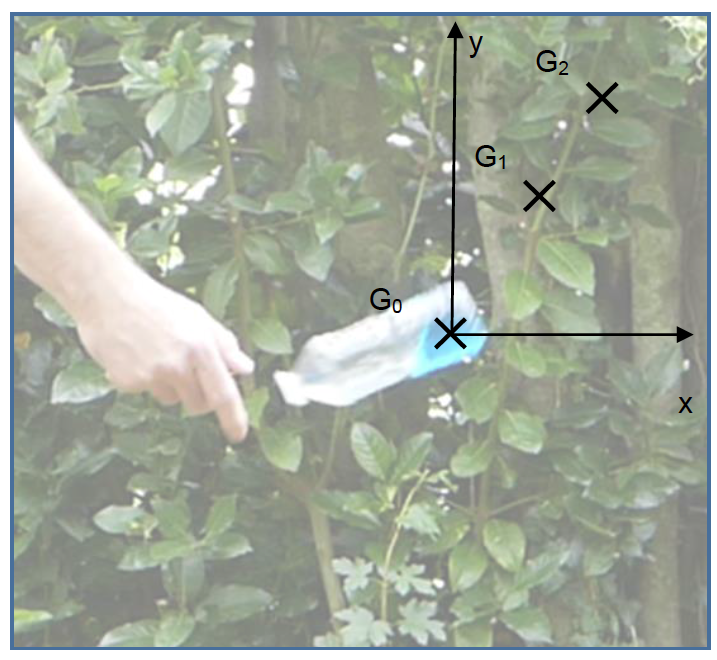
Grâce à la vidéo montrant un lancer réussi, on a pu pointer la position du centre de masse G à différents instants.
Sur la figure 2, la durée entre deux positions successives est 𝜏 = 40 ms.
L’échelle est donnée par la bouteille dont la hauteur est 18,8 cm.
1. Représenter sur la copie, sans souci d’échelle, le système d’axes (Oxy), le vecteur ![]() , l’angle 𝛼 ainsi que les coordonnées 𝑣0x et 𝑣0y et l’allure de la trajectoire du centre de masse de la bouteille.
, l’angle 𝛼 ainsi que les coordonnées 𝑣0x et 𝑣0y et l’allure de la trajectoire du centre de masse de la bouteille.
2. À partir des données expérimentales fournies et de la figure 2, vérifier que la valeur expérimentale 𝑣0 du vecteur vitesse initial ![]() est proche de 3,6 m⋅s−1.
est proche de 3,6 m⋅s−1.
3. Proposer une méthode permettant de déterminer expérimentalement la valeur de l’angle 𝛼.
Modélisation du déplacement du centre de masse
4. En précisant la loi utilisée, donner les expressions des coordonnées du vecteur accélération 𝑎⃗ du centre de masse : ax(𝑡) et ay(𝑡).
Réponse :
Système {bouteille + eau}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
![]()
![]()
![]()
![]()
Or
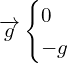
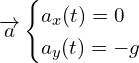
5. En déduire les expressions des coordonnées 𝑣x(𝑡) et 𝑣y(𝑡) du vecteur vitesse du centre de masse et montrer que les équations horaires du mouvement sont :
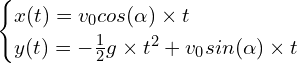
Réponse :
![]()
On intègre le système d’équation précédent :
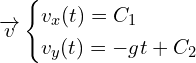
Pour trouver les constantes, on utilise ![]() :
:
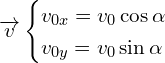
d’ou
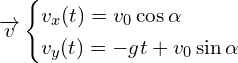
![]()
On intègre le système d’équation précédent :
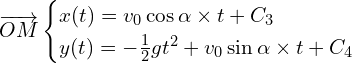
Pour trouver les constantes, on utilise ![]()
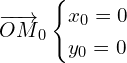
d’ou
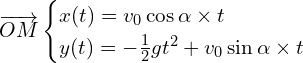
Pour déterminer la distance à laquelle tombe la bouteille par rapport au point O, on crée un programme en langage python dont un extrait est présenté ci-dessous. Ce programme utilise les équations horaires modélisant le déplacement du centre de masse et les valeurs expérimentales :
𝑣0 = 3,6 m⋅s−1 𝛼 = 59 ° g = 9,81 m ⋅ s−2
| 5. | g = 9.81 # Intensité du champ de pesanteur en m /s2 |
| 6. | |
| 7. | v0 = float(input(‘valeur de la vitesse initiale(en m/s) : v0 = ‘) |
| 8. | alpha = float(input(‘valeur de l’angle de tir(en degré) : alpha = ‘) |
| 9. | |
| 10. | # Tracé des courbes horaires |
| 11. | |
| 12. | t=np.linspace(0,0.65,100) |
| 13. | for i in t : |
| 14. | x = v0*cos(alpha*pi/180)*t #calcul de x à la date t |
| 15. | y = -0.5*g*t**2+ *t #calcul de y à la date t |
| 16. | |
| 17. | plt.plot(t,x,’k–‘,label=’x en fonction de t’) |
| 18. | plt.plot(t,y,’k’,label=’y en fonction de t’) |
| 19. |
L’exécution de ce programme permet d’obtenir le graphique ci-dessous qui modélise l’évolution des coordonnées (x,y), exprimées en mètre, du point G au cours du temps.
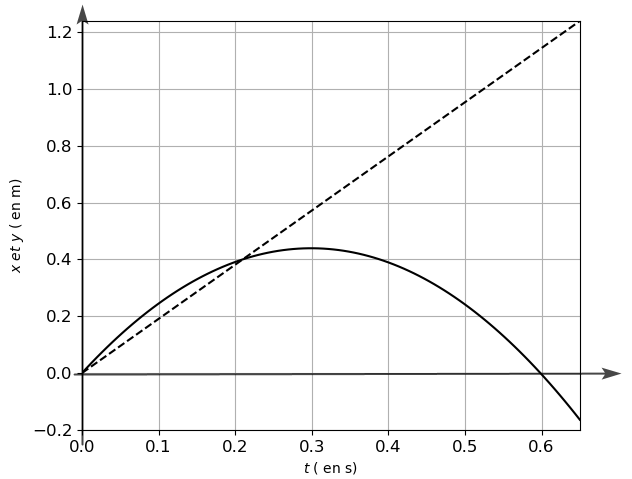
6. Associer chacun de ces tracés à x(𝑡) et y(𝑡).
7. Préciser ce qui est caché par le rectangle gris dans la ligne 15 du programme (expression ou valeur). On estime que le centre de masse G se trouve à une hauteur voisine de 2 cm du fond de la bouteille lorsque celle-ci se pose sur la table.
8. Estimer la durée du mouvement de la bouteille obtenue par la modélisation.
La durée du mouvement de la bouteille lors de la réalisation de ce « water bottle flip » a été mesurée. On a obtenu Δ𝑡 = (0,50 ± 0,05) s.
9. Proposer au moins une explication permettant de rendre compte de l’écart entre cette durée réelle et la durée obtenue par la modélisation.
10. À l’aide du modèle, déterminer la distance à laquelle la bouteille tombe sur la table par rapport à l’origine du repère. Indiquer ce qu’il est possible de prévoir pour la distance réelle.
