Métropole 2025 Sujet 2 Bis
Exercice 1 – (9 points) – Durée 1h35 – Calculatrice autorisée
Sujet n°25-PYCJ2ME4
Sujet et corrigé
Exercice 1 – Savon : parfum, synthèse et utilisation (9 points)
Le savon est un produit d’hygiène connu depuis l’Antiquité. Au cours des siècles, son procédé de fabrication et sa composition ont évolué. En effet, de nombreux savons contiennent, de nos jours, des additifs comme des parfums.
Les objectifs de cet exercice sont :
- d’étudier la réaction d’estérification conduisant à la formation de l’éthanoate de linalyle, espèce à l’odeur de lavande utilisée dans certains savons, et d’améliorer le rendement de cette réaction ;
- d’étudier le mécanisme réactionnel d’une synthèse d’un savon ;
- de discuter de l’influence de la dureté de l’eau sur le pouvoir moussant d’un savon.
1. Utilisation de l’acide éthanoïque pour la synthèse de l’éthanoate de linalyle
Données :
- formule semi-développée de l’éthanoate de linalyle :
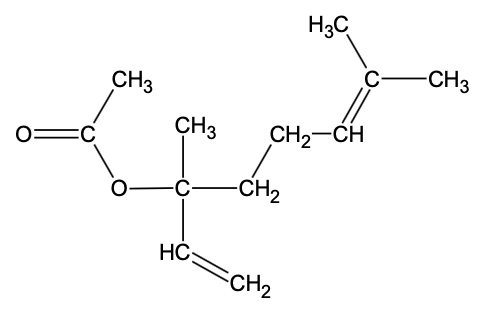
- propriétés physico-chimiques de différentes espèces chimiques :
| Nom de l’espèce chimique | Acide éthanoïque | Linalol | Éthanoate de linalyle |
| Formule brute | C2H4O2 | C10H18O | C12H20O2 |
- couple acide-base acide éthanoïque / ion éthanoate : C2H4O2(aq)/C2H3O–(aq)
- produit ionique de l’eau à 25 °C : Ke = 1,0×10–14 ;
- concentration standard : c° = 1 mol·L–1.
Q1. Représenter la formule topologique de l’éthanoate de linalyle, puis entourer le groupe caractéristique de cette molécule et nommer la famille fonctionnelle correspondante.

Famille fonctionnelle correspondante : Ester.
L’éthanoate de linalyle est synthétisé en faisant réagir du linalol avec de l’acide éthanoïque. L’équation de la réaction modélisant cette transformation chimique, appelée estérification, est :
C2H4O2(ℓ) + C10H18O(ℓ) ⇌ C12H20O2(ℓ) + H2O(ℓ)
Cette synthèse est une transformation chimique lente et non totale. On souhaite étudier l’évolution temporelle de l’avancement, noté x, de cette réaction. Pour cela, on titre la quantité de matière d’acide éthanoïque restant dans le milieu réactionnel, par une solution aqueuse d’hydroxyde de sodium à différentes dates t au cours de la transformation.
Q2. Écrire l’équation de la réaction support du titrage.
On titre la quantité de matière d’acide éthanoïque restant dans le milieu réactionnel, par une solution aqueuse d’hydroxyde de sodium
$$C_2H_4O_2\left(aq\right)+{\rm HO}^-\left(aq\right)\rightarrow{C_2H_3O}_2^-\left(aq\right)+\ H_2O(l)$$
Préalablement à cette expérience, on cherche à vérifier le caractère total de la transformation support du titrage. Pour cela, on introduit un volume VB = 5,0 mL d’une solution aqueuse d’hydroxyde de sodium de concentration cB = 1,0×10–2 mol·L–1 dans un volume VA = 50,0 mL d’une solution d’acide éthanoïque. Dans ces conditions, l’acide éthanoïque est en excès. Le pH du mélange à 25°C est de 4,6.
Q3. Calculer, en utilisant la valeur de Ke, la concentration finale en quantité de matière en ions hydroxyde, notée [OH–]f, dans ce mélange de volume VA + VB. En déduire que la quantité de matière nf(OH–) à l’état final dans le mélange est d’environ 2,2×10–11 mol.
$$K_e=\frac{\left[H_3O^+\right]_f\times \left[{\rm HO}^-\right]_f}{{{(c}^0)}^2}$$
$$\frac{\left[H_3O^+\right]_f\times \left[{\rm HO}^-\right]_f}{{{(c}^0)}^2}=K_e$$
$$\left[{\rm HO}^-\right]_f=\frac{K_e\times {{(c}^0)}^2}{\left[H_3O^+\right]_f}$$
Or
$$\left[H_3O^+\right]=c^0\times {10}^{-pH}$$
D’ou
$$\left[{\rm HO}^-\right]_f=\frac{K_e\times {{(c}^0)}^2}{c^0\times {10}^{-pH}}$$
$$\left[{\rm HO}^-\right]_f=\frac{K_e\times c^0}{{10}^{-pH}}$$
$$\left[{\rm HO}^-\right]_f=\frac{{10}^{-14}\times 1}{{10}^{-4,6}}$$
$$\left[{\rm HO}^-\right]_f=4,0{\times 10}^{-10}\ mol{.L}^{-1}$$
$$\left[{\rm HO}^-\right]_f=\frac{n_f\left({\rm HO}^-\right)}{V_A+V_B}$$
$$\frac{n_f\left({\rm HO}^-\right)}{V_A+V_B}=\left[{\rm HO}^-\right]_f$$
$$n_f\left({\rm HO}^-\right)=\left[{\rm HO}^-\right]_f\times \left(V_A+V_B\right)$$
$$n_f\left({\rm HO}^-\right)=4,0{\times 10}^{-10}\times \left(50,0{\times 10}^{-3}+5,0{\times 10}^{-3}\right)$$
$$n_f\left({\rm HO}^-\right)=2,2{\times 10}^{-11}mol$$
Q4. Comparer cette valeur à celle de la quantité d’ions hydroxyde introduite initialement puis commenter. On admet qu’on peut généraliser ce résultat à tout moment du titrage.
Calculons la quantité d’ions hydroxyde introduite initialement :
$$c_B=\frac{n_i\left({\rm HO}^-\right)}{V_B}$$
$$\frac{n_i\left({\rm HO}^-\right)}{V_B}=c_B$$
$$n_i\left({\rm HO}^-\right)=c_B\times V_B$$
$$n_i\left({\rm HO}^-\right)=1,0{\times 10}^{-2}\times 5,0{\times 10}^{-3}$$
$$n_i\left({\rm HO}^-\right)=5,0{\times 10}^{-5}\ mol$$
Comparons la quantité de matière d’ions hydroxyde à l’état initiale à celle finale :
$$\frac{n_i\left({\rm HO}^-\right)}{n_f\left({\rm HO}^-\right)}=\frac{5,0{\times 10}^{-5}}{2,2{\times 10}^{-11}}$$
$$\frac{n_i\left({\rm HO}^-\right)}{n_f\left({\rm HO}^-\right)}=2,3{\times 10}^6$$
La quantité de matière d’ions hydroxyde à l’état initiale est très supérieure à celle finale : la réaction est totale.
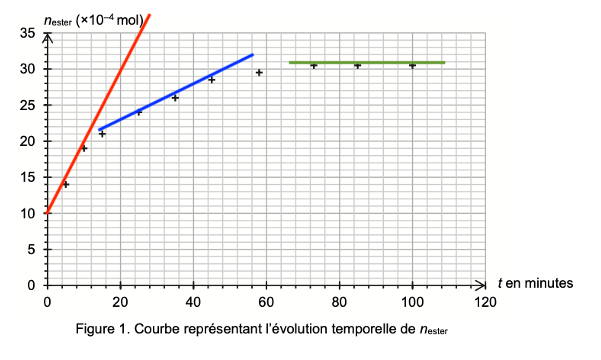
On effectue expérimentalement le suivi temporel de l’estérification. Les résultats obtenus permettent de représenter l’évolution de la quantité de matière d’éthanoate de linalyle formé, notée nester, au cours du temps (figure 1).

Figure 1. Courbe représentant l’évolution temporelle de nester
Q5. Exprimer la vitesse volumique d’apparition de l’éthanoate de linalyle, notée vester, en fonction du volume V du milieu réactionnel et de nester.
$$v_{ester}=\frac{d\left[Ester\right]_{(t)}}{dt}$$
Or
$$\left[Ester\right]{(t)}=\frac{n{ester}}{V}$$
D’où
$$v_{ester}=\frac{d\frac{n_{ester}}{V}}{dt}$$
$$v_{ester}=\frac{1}{V}\times \frac{dn_{ester}}{dt}$$
Q6. Décrire, en justifiant, l’évolution de la vitesse volumique d’apparition de l’éthanoate de linalyle au cours du temps. Proposer un facteur cinétique à l’origine de cette évolution.
$$v_{ester}=\frac{1}{V}\times \frac{dn_{ester}}{dt}$$
La dérivée se calcul en trouvant le coefficient directeur de la tangente en un point de la courbe.
Graphiquement, le coefficient directeur de la tangente diminue au cours du temps. Ainsi, la vitesse volumique d’apparition de l’éthanoate de linalyle diminue au cours du temps.
Un facteur cinétique à l’origine de cette évolution est la concentration.
Au cours de la réaction, la concentration des réactifs diminue. Ainsi, la vitesse volumique d’apparition de l’éthanoate de linalyle diminue au cours du temps.
Le rendement de cette synthèse est faible. Afin de l’améliorer, il est possible d’envisager un montage permettant l’élimination de l’eau produite au cours de la réaction. Le système étant homogène, on admet que la constante d’équilibre K de la réaction d’estérification s’écrit :
$$ K = \frac{n(\mathrm{C}_{12}\mathrm{H}_{20}\mathrm{O}_2)_{\text{éq}} \cdot n(\mathrm{H_2O})_{\text{éq}}}{n(\mathrm{C_2H_4O_2})_{\text{éq}} \cdot n(\mathrm{C_{10}H_{18}O})_{\text{éq}}} $$
où n(X)éq représente la quantité de matière de l’espèce X dans le milieu réactionnel à l’équilibre chimique.
Q7. Expliquer en quoi l’élimination de l’eau au cours de la synthèse permet d’améliorer le rendement.
$$K=\frac{{n\left(C_{12}H_{20}O_2\right)}{eq}\times {n\left(H_2O\right)}{eq}}{{n\left(C_2H_4O_2\right)}{eq}\times {n\left(C{10}H_{18}O\right)}{eq}}$$
$$Qr=\frac{n\left(C{12}H_{20}O_2\right)\times n\left(H_2O\right)}{n\left(C_2H_4O_2\right)\times n\left(C_{10}H_{18}O\right)}$$
En éliminant l’eau au cours de la synthèse, Qr=0.
Ainsi, Qr sera toujours inferieur à K. L’état d’équilibre ne sera jamais atteint : la réaction se déroulera dans le sens direct. La réaction sera totale.
Ainsi, l’élimination de l’eau au cours de la synthèse permet d’améliorer le rendement.
2. Utilisation de l’anhydride éthanoïque pour la synthèse de l’éthanoate de linalyle
Données :
- propriétés physico-chimiques de différentes espèces chimiques :
| Nom de l’espèce chimique | Anhydride éthanoïque | Linalol | Éthanoate de linalyle | Acide éthanoïque | Eau |
| Formule brute | C4H6O3 | C10H18O | C12H20O2 | C2H4O2 | H2O |
| Masse volumique g·mL–1 | 1,08 | 0,87 | 0,89 | 1,05 | 1,00 |
| Masse molaire en g·mol–1 | 102 | 154 | 196 | 60 | 18 |
| Solubilité dans l’eau | Bonne | Assez faible | Très faible | Très bonne |
L’éthanoate de linalyle peut également être synthétisé à partir d’anhydride éthanoïque et de linalol. Cette transformation est totale et peut être modélisée par l’équation de réaction suivante :
C4H6O3(ℓ) + C10H18O(ℓ) → C12H20O2(ℓ) + C2H4O2(ℓ)
On réalise la synthèse de l’éthanoate de linalyle en suivant les étapes du protocole décrites ci-dessous :
Étape n°1 :
- à la date t = 0, introduire 10 mL de linalol et 10 mL d’anhydride éthanoïque dans un ballon sec ;
- agiter et chauffer le mélange à l’aide d’un montage à reflux pendant une durée de 30 min.
Étape n°2 :
- verser doucement 30 mL d’eau distillée dans le ballon, par le sommet du réfrigérant. L’excès d’anhydride éthanoïque est alors totalement transformé en acide éthanoïque ;
- transvaser le contenu du ballon refroidi dans une ampoule à décanter et laisser décanter le mélange.
Étape n°3 :
- récupérer la phase organique et la traiter pour éliminer les impuretés restantes.
Q8. Indiquer, en justifiant, la nature et la position de la phase dans laquelle se trouve l’éthanoate de linalyle à la fin de l’étape n°2.
Étape n°2 : – verser doucement 30 mL d’eau distillée
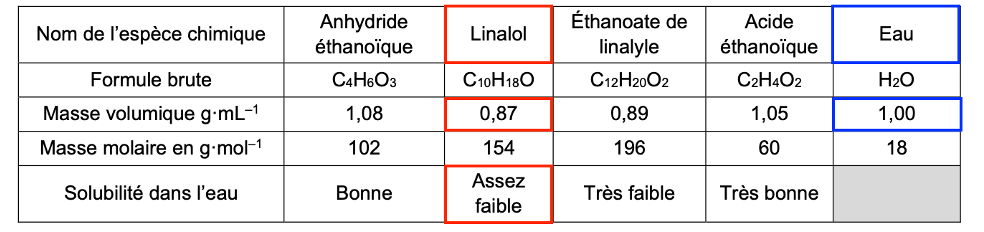
D’après le tableau l’éthanoate de linalyle est très faiblement soluble dans l’eau. Il ne se trouve donc dans l’eau. Il se trouve dans la phase organique.
La masse volumique de l’éthanoate de linalyle 0,89 g.mL-1 est plus faible que celle de l’eau 1,00 g.mL-1. Ainsi l’éthanoate de linalyle est situé au-dessus.
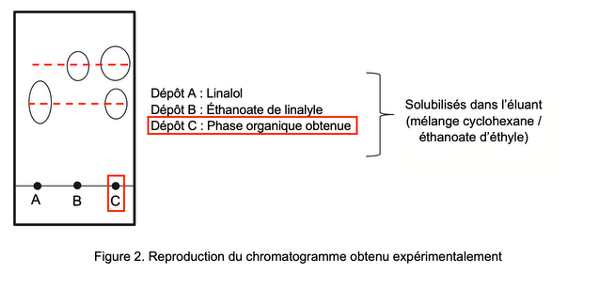
Pour vérifier la composition de la phase organique, on l’analyse à l’aide d’une chromatographie sur couche mince. Après révélation à l’aide d’une solution de permanganate de potassium, on obtient le chromatogramme reproduit sur la figure 2.

Solubilisés dans l’éluant (mélange cyclohexane / éthanoate d’éthyle)
Dépôt A : Linalol
Dépôt B : Éthanoate de linalyle
Dépôt C : Phase organique obtenue
Figure 2. Reproduction du chromatogramme obtenu expérimentalement
Q9. Identifier, en justifiant, les espèces présentes dans la phase organique. Commenter.
Le dépôt C (phase organique obtenue) montre 2 taches. Une des taches est au même niveau que le linalol et l’autre est au même niveau que l’éthanoate de linalyle.
Ainsi, les espèces présentes dans la phase organique sont le linalol et l’éthanoate de linalyle.
La synthèse est réalisée une seconde fois en conservant l’ensemble des paramètres expérimentaux (température, durée de l’expérience, quantités de matière initiales), mais en ajoutant une très faible quantité d’un acide, l’APTS (acide paratoluènesulfonique), dans le ballon lors de l’étape 1. Le volume de la phase organique alors recueillie est de 9,4 mL et le chromatogramme obtenu est reproduit sur la figure 3.
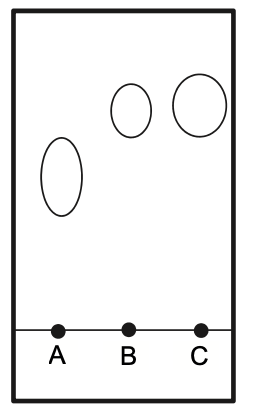
Solubilisés dans l’éluant (mélange cyclohexane / éthanoate d’éthyle)
Dépôt A : Linalol
Dépôt B : Éthanoate de linalyle
Dépôt C : Phase organique obtenue
Figure 3. Chromatogramme obtenu expérimentalement après la deuxième synthèse
Q10. Déterminer l’intérêt de l’ajout d’APTS dans le milieu réactionnel.
Avec l’ajout d’APTS dans le milieu réactionnel, Le dépôt C (phase organique obtenue) montre une tache qui est au même niveau que l’éthanoate de linalyle.
Une seule espèce est présente dans la phase organique : l’éthanoate de linalyle.
Ainsi, l’ajout d’APTS dans le milieu réactionnel permet de rendre insoluble le linalol dans la phase organique.

Q11. Après avoir montré que le linalol est le réactif limitant dans la transformation chimique étudiée, calculer le rendement de la synthèse avec ajout d’APTS.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.
Calculons les quantités initiales des réactifs :
$$n=\frac{m}{M}$$
Or
$$\rho=\frac{m}{V}$$
$$\frac{m}{V}=\rho$$
$$m=\rho\times V$$
$$n=\frac{\rho\times V}{M}$$
Ainsi :
$$n_{linalol}=\frac{\rho_{linalol}\times V_{linalol}}{M_{linalol}}$$
$$n_{linalol}=\frac{0,87\times 10}{154}$$
$$n_{linalol}=5,6\times {10}^{-2}\ mol$$
$$n_{anhydrique\ ethanoique}=\frac{\rho_{anhydrique\ ethanoique}\times V_{anhydrique\ ethanoique}}{M_{anhydrique\ ethanoique}}$$
$$n_{anhydrique\ ethanoique}=\frac{1,08\times 10}{102}$$
$$n_{anhydrique\ ethanoique}=1,1\times {10}^{-1}\ mol$$
$$C_2H_6O_3\left(aq\right)+C_{10}H_{18}O\left(aq\right)\rightarrow C_{12}H_{20}O_2\left(aq\right)+\ C_2H_4O_2\left(aq\right)$$
$$C_2H_6O_3\left(aq\right)∶anhydrique\ éthanoique\ et\ C_{10}H_{18}O\left(aq\right)∶linalol$$
$$x_{max1}=\frac{n_{anhydrique\ ethanoique}}{1}=\frac{1,1\times {10}^{-1}}{1}=1,1\times {10}^{-1}\ mol$$
$$x_{max2}=\frac{n_{linalol}}{1}=\frac{5,6\times {10}^{-2}}{1}=5,6\times {10}^{-2}\ mol$$
$x_{max2}<x_{max1} : x_{max}=x_{max2}=5,6\times{10}^{-2}\ mol$, le linalol est le réactif limitant ans la transformation chimique étudiée.
Calcul du rendement de la synthèse avec ajout d’APTS.
$$\eta=\frac{n_{ethanoate\ de\ linalyle}^{exp}}{n_{ethanoate\ de\ linalyle}^{th}}$$
Avec :
$$n_{ethanoate\ de\ linalyle}^{th}=x_{max}$$
$$n_{ethanoate\ de\ linalyle}^{th}=5,6\times {10}^{-2}\ mol$$
$$n_{ethanoate\ de\ linalyle}^{exp}=\frac{\rho_{ethanoate\ de\ linalyle}\times V_{ethanoate\ de\ linalyle}}{M_{ethanoate\ de\ linalyle}}$$
$$n_{ethanoate\ de\ linalyle}^{exp}=\frac{0,89\times 9,4}{196}$$
$$n_{ethanoate\ de\ linalyle}^{exp}=4,3\times {10}^{-2}\ mol$$
$$\eta=\frac{n_{ethanoate\ de\ linalyle}^{exp}}{n_{ethanoate\ de\ linalyle}^{th}}$$
$$\eta=\frac{4,3\times {10}^{-2}}{5,6\times {10}^{-2}}$$
$$\eta=0,77$$
$$\eta=77%$$
Le rendement de la synthèse avec ajout d’APTS est de 77%.
3. Synthèse et pouvoir moussant d’un savon – Dureté d’une eau
Données :
- la dureté de l’eau ou titre hydrotimétrique (TH) est essentiellement due à la présence d’ions calcium Ca2+ et magnésium Mg2+. Elle s’exprime en degré français (°f) et s’obtient par la relation :
TH = 104·[X2+]
où [X2+] représente la somme des concentrations en quantité de matière des ions calcium et magnésium exprimées en mol·L–1 ;
- plage de valeurs du titre hydrotimétrique (TH) et qualificatif de l’eau associée :
| TH (°f) | 0 à 7 | 7 à 15 | 15 à 30 | 30 à 40 | plus de 40 |
| Eau | très douce | douce | moyennement dure | dure | très dure |
- électronégativité de quelques atomes :
| Atome | C | O | H |
| Électronégativité | 2,6 | 3,4 | 2,2 |
Formation d’un savon
L’une des principales applications de l’hydrolyse basique d’un ester est la synthèse des savons. L’hydrolyse basique d’un ester est une transformation chimique, lente et totale, au cours de laquelle un alcool et un ion carboxylate sont obtenus par réaction entre un ester et un ion hydroxyde OH–. Le mécanisme de cette réaction se décompose en trois étapes présentées ci-dessous, où R1 et R2 représentent des chaînes carbonées :
- Première étape :

- Deuxième étape :
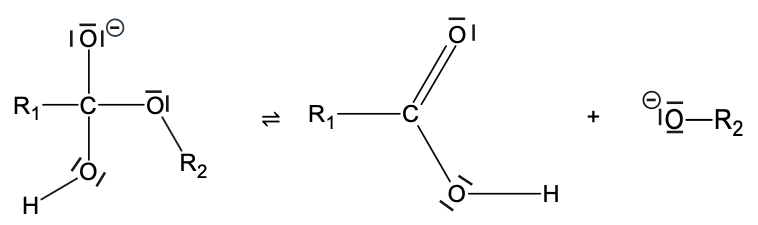
- Troisième étape :

Q12. Identifier, en justifiant à l’aide des électronégativités, le site accepteur d’électrons (site électrophile) de la molécule d’ester.
L’électronégativité de l’atome d’oxygène est supérieure à celle du carbone.
Les atomes d’oxygène sont donneurs d’électrons et l’atome de carbone est site accepteur d’électrons (site électrophile) de la molécule d’ester.

Q13. Recopier la première étape du mécanisme sur la copie, puis la compléter à l’aide de flèches courbes.
Lors d’une formation de liaison, le doublet d’électrons se déplace du site donneur (ici l’atome d’oxygène qui possède une charge négative) vers le site accepteur (ici l’atome de carbone).
Lors d’une rupture de liaison, la flèche part de la liaison vers l’atome le plus électronégatif (ici l’atome d’oxygène).
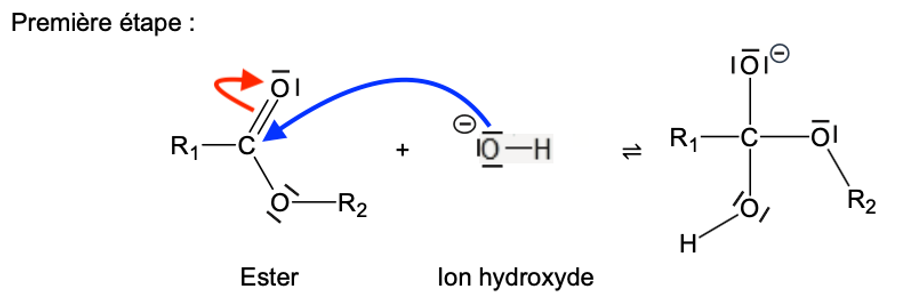
Q14. Indiquer, pour chacune des trois étapes, le type de réaction mise en jeu.
Première étape : Addition
Deuxième étape : Élimination
Troisième étape : réaction Acide base
Dureté d’une eau et pouvoir moussant d’un savon
En présence d’ions calcium Ca2+ et magnésium Mg2+, les ions carboxylate présents dans un savon forment un précipité entraînant la diminution de son pouvoir moussant. La dureté de l’eau influe donc sur l’efficacité d’un savon.
On détermine la dureté d’une eau à l’aide d’un titrage colorimétrique des ions Ca2+ et Mg2+, notés indifféremment X2+, suivant le protocole expérimental décrit ci-dessous :
- introduire un volume Veau = 50,00 mL d’eau à étudier dans un erlenmeyer (incertitude-type associée : u(Veau) = 0,03 mL) ;
- ajouter 20 mL de solution tampon de pH = 10 et quelques gouttes d’un indicateur coloré ;
- doser la solution contenue dans l’erlenmeyer, par une solution aqueuse d’EDTA disodique (2 Na+(aq) ; H2Y2–(aq)) de concentration c = 5,00×10–3 mol·L–1 (incertitude-type associée : u(c) = 0,06×10–3 mol·L–1).
Le volume à l’équivalence VE = 17,6 mL est repéré par le changement de couleur de l’indicateur coloré. L’incertitude-type associée à ce volume est : u(VE) = 0,1 mL.
Dans ces conditions, l’EDTA réagit avec les ions calcium et magnésium contenus dans l’eau selon l’équation support de titrage suivante :
X2+(aq) + H2Y2–(aq) → XY2–(aq) + 2 H+(aq)
Q15. Établir que la relation suivante est vérifiée à l’équivalence du titrage :
$$[X^{2+}] = \dfrac{c \cdot V_E}{V_{\text{eau}}}$$
$$X^{2+}\left(aq\right)+{H_2Y}^{2-}\left(aq\right)\rightarrow {\rm XY}^{2-}\left(aq\right)+\ 2H^+\left(aq\right)$$
A l’équivalence :
$$\frac{n_{X^{2+}}^i}{1}=\frac{n_{{H_2Y}^{2-}}^{eq}}{1}$$
$$\left[X^{2+}\right]\times V_{eau}=c\times V_E$$
$$\left[X^{2+}\right]=\frac{c\times V_E}{V_{eau}}$$
Q16. Calculer la valeur du titre hydrotimétrique TH de l’eau étudiée, puis déterminer l’incertitude-type u(TH) associée à cette mesure, sachant que :
$$u(TH) = TH \cdot \sqrt{\left(\dfrac{u(V_E)}{V_E}\right)^2 + \left(\dfrac{u(c)}{c}\right)^2 + \left(\dfrac{u(V_{\text{eau}})}{V_{\text{eau}}}\right)^2}$$
Calculons la valeur du titre hydrotimétrique TH de l’eau étudiée
D’après les données : la dureté de l’eau ou titre hydrotimétrique (TH) est essentiellement due à la présence d’ions calcium Ca2+ et magnésium Mg2+. Elle s’exprime en degré français (°f) et s’obtient par la relation : TH = 104·[X2+]
$$TH={10}^4\times \left[X^{2+}\right]$$
Or
$$\left[X^{2+}\right]=\frac{c\times V_E}{V_{eau}}$$
D’où
$$TH={10}^4\times \frac{c\times V_E}{V_{eau}}$$
$$TH={10}^4\times \frac{5,00\times {10}^{-3}\times 17,6\times {10}^{-3}}{50,00\times {10}^{-3}}$$
$$TH=17,6\ °f$$
Déterminons l’incertitude-type u(TH) associée à cette mesure :
$$u(TH)=TH\times \sqrt{\left(\frac{u(V_E)}{V_E}\right)^2+\left(\frac{u(c)}{c}\right)^2+\left(\frac{u(V_{eau})}{V_{eau}}\right)^2}$$
$$u(TH)=17,6\times \sqrt{\left(\frac{0,1}{17,6}\right)^2+\left(\frac{0,06\times {10}^{-3}}{5,00\times {10}^{-3}}\right)^2+\left(\frac{0,03}{50,00}\right)^2}$$
$$u(TH)=0,3$$
Q17. Comparer, en justifiant, le pouvoir moussant d’un savon dans l’eau titrée avec celui dans une eau dont la dureté serait de 30 °f.
L’eau titrée à une dureté de 17,6 °f.
D’après l’énoncé :
- La dureté de l’eau ou titre hydrotimétrique (TH) est essentiellement due à la présence d’ions calcium Ca2+ et magnésium Mg2+
- En présence d’ions calcium Ca2+ et magnésium Mg2+, les ions carboxylate présents dans un savon forment un précipité entraînant la diminution de son pouvoir moussant.
Ainsi, le pouvoir moussant d’un savon dans l’eau titrée est supérieur à celui dans une eau dont la dureté serait de 30 °f.
