Polynésie 2025 Sujet 1
Exercice 2 – (6 points) – Durée 1h03 – Calculatrice autorisée
Sujet n°25-PYCJ1PO1
Le Mölkky, créé en 1996, est un jeu de plein air originaire de Finlande.
Dans ce jeu, le joueur de Mölkky doit faire tomber des quilles en bois, à l’aide d’un bâton, afin d’atteindre un score de 50 points. Une quille tombée lui donnera le nombre de points porté sur cette dernière compris entre 1 et 12. Plusieurs quilles tombées donneront au joueur le nombre de points correspondant au nombre de quilles au sol.
D’après « cdsmr85.org »
L’objectif de cet exercice est d’établir l’équation horaire de la trajectoire du bâton lancé et de déterminer le lieu d’impact au sol afin de prévoir une éventuelle victoire d’un joueur.
On s’intéresse au mouvement du centre de masse G du bâton lorsqu’un joueur le lance afin de faire tomber une quille. L’étude est réalisée dans le référentiel terrestre supposé galiléen et on considère qu’une fois lancé, le bâton n’est soumis qu’à son poids. Pour simplifier, on suppose que le bâton ne tourne pas sur lui-même. La masse du bâton est notée m.
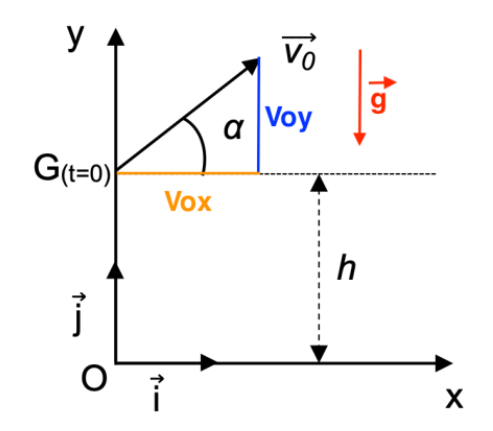
Quand le bâton quitte la main du joueur, son centre de masse G est situé à une hauteur h par rapport au sol avec un vecteur vitesse initial $\overrightarrow{v_0}$ qui forme un angle α avec l’horizontale.
On étudie le mouvement du centre de masse du système {bâton} dans le repère cartésien indiqué sur la figure 1.
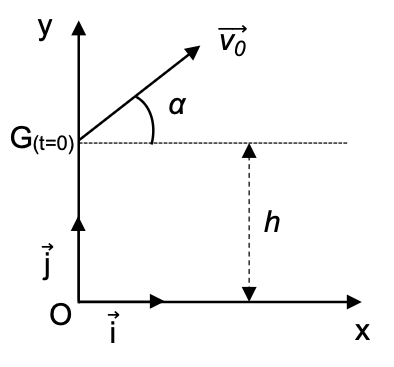
Figure 1. Schéma de la situation du lancer du bâton de Mölkky.
Q1. Énoncer la deuxième loi de Newton et l’utiliser pour établir les expressions des coordonnées notées ax(t) et ay(t) du vecteur accélération a⃗(t) du point G selon les axes (Ox) et (Oy).
Q2. Établir les expressions des coordonnées horizontales notée vx(t) et verticale vy(t) du vecteur vitesse $\overrightarrow{v}(t)$ du point G
Q3. À partir des expressions des coordonnées de la vitesse vx(t) et vy(t) et de la figure 1, établir que les équations horaires du mouvement x(t) et y(t) du point G sont :
$$x(t) = v_0 \cdot \cos(\alpha)\cdot t$$
$$y(t) = – \frac{1}{2} g\cdot t^2 + v_0 \cdot \sin(\alpha)\cdot t + h$$
Donnée :
- vitesse initiale de lancer du bâton de Mölkky : v0 = 4,9 m·s–1 ;
- hauteur depuis laquelle le bâton est lancé : h = 0,70 m ;
- angle avec lequel le bâton est lancé par rapport à l’horizontale : α = 30° ;
- intensité du champ de pesanteur terrestre g = 9,8 m·s–2.
Q4. À l’aide des données et des équations horaires du mouvement, montrer que l’expression de l’équation de la trajectoire y(x), x et y étant exprimés en mètres, s’écrit sous la forme :
y(x) = – 0,27 x2 + 0,58 x + 0,70
Un joueur ayant déjà marqué 41 points s’apprête à lancer le bâton de Mölkky. Pour gagner, il doit atteindre exactement le score de 50 points. La configuration du jeu est représentée sur la photographie de la figure 2.
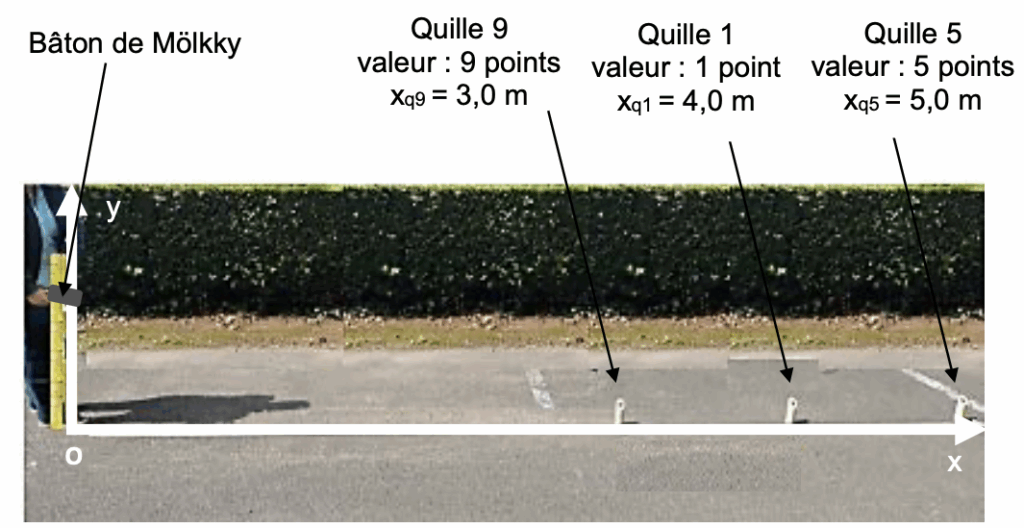
Figure 2. Photographie de la configuration du jeu avant le lancer.
Dans notre étude, la taille des quilles est considérée comme négligeable au regard des distances mises en jeu. On assimilera alors la quille à un point posé au sol.
On suppose qu’il n’y a pas de rebond du bâton à la suite du lancer.
Dans la question suivante, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
Q5. Vérifier que la partie est remportée par le joueur si le lancer est réalisé dans les conditions précisées dans les données précédentes.
Sur la figure 3, on a reproduit un extrait d’un programme Python qui permet de calculer puis de tracer les courbes représentant l’énergie cinétique EC, l’énergie potentielle de pesanteur EP et l’énergie mécanique Em du bâton de Mölkky lors de son lancer. Les données numériques utilisées sont identiques aux questions précédentes.
| […] 14 Ecl=[ ] 15 Epl=[ ] 16 Eml=[ ] 17 for i in range(len(tl)) : 18 Ec=0.5*0.4*(vxl[i]**2+vyl[i]**2) 19 Ecl.append(Ec) 20 Ep=0.4*9.81*y[i] 21 Epl.append(Ep) 22 Em=___________ 23 Eml.append(Em) […] |
Figure 3. Extrait du programme Python permettant de tracer les différentes énergies du bâton de Mölkky en fonction du temps (Ecl, Epl, Eml sont exprimées en J ; vx, vy sont exprimées en m·s–1 ; y est exprimé en m).
Q6. À partir de la figure 3, déterminer la masse m du bâton de Mölkky. Justifier la réponse.
Q7. Écrire et compléter, sur votre copie, la ligne 22 du programme de la figure 3 qui permet de calculer l’énergie mécanique Em du bâton de Mölkky.
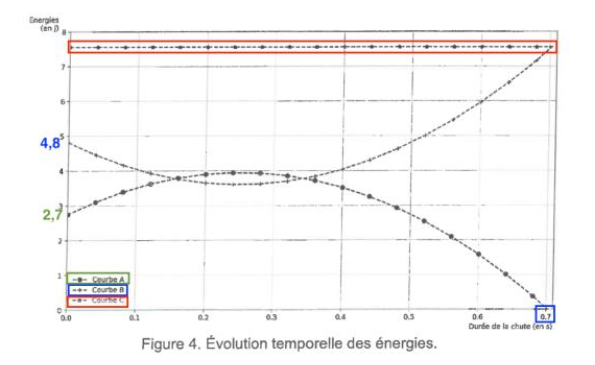
La figure 4 représente les courbes affichées après avoir exécuté le programme Python complet.
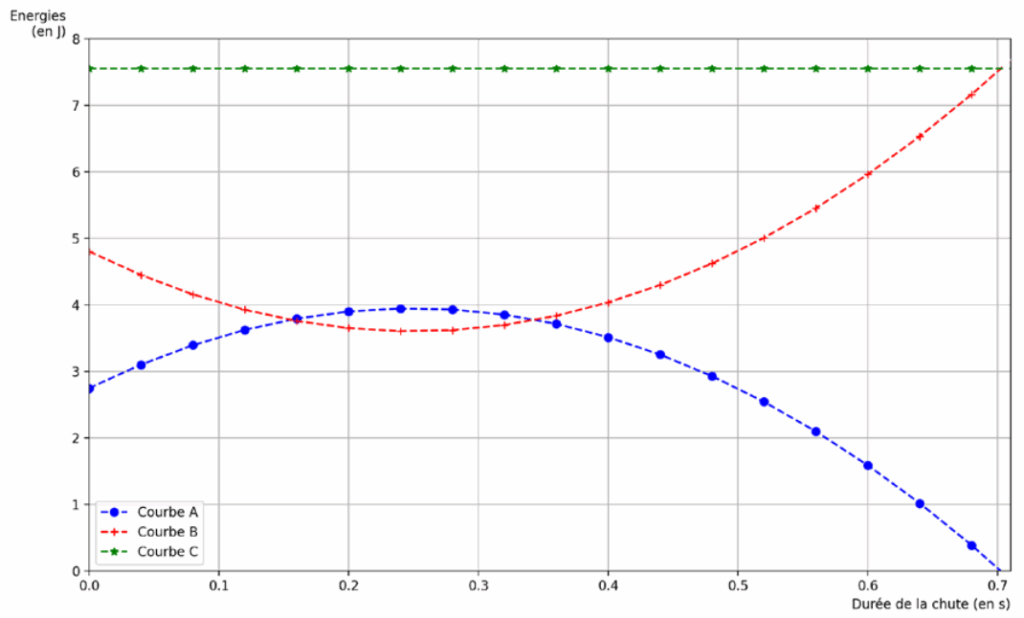
Figure 4. Évolution temporelle des énergies.
Q8. Attribuer chaque courbe de la figure 4 à l’énergie représentée. Justifier la réponse.
Q9. Déterminer la « durée de vol » du bâton de Mölkky (durée de chute) et en déduire que la partie décrite précédemment est remportée par le joueur, en considérant les équations horaires du mouvement établies dans la question Q3.